GRAĐEVINSKI FAKULTET SVEUČILIŠTA U ZAGREBU KAČIĆEVA 26
SEMINARSKI
RAD IZ KOLEGIJA EKSPERIMENTALNE METODE I
Tema : ISPITIVANJA IZOTROPNIH I ANIZOTROPNIH MATERIJALA
Gadaf Zulbeari , 2867
1.Vrste materijala
Tvar tj. materija
sastoji se od diskretnih čestica (molekula i atoma) na vrlo malim razmacima u
pravilnom ili nepravilnom rasporedu u prostoru. Obzirom na raspored tih čestica
u prostoru osnovni oblici strukture čvrstih materijala su kristalna, amorfna
i polikristalna struktura.
Kod materijala s kristalnom
strukturom diskretne čestice raspoređene su u prostoru po nekakvom pravilu tako da
formiraju prostorne kristalne rešetke. Kristali u osnovi mogu imati takav
raspored molekula
da su fizikalna svojstva u svim smjerovima jednaka (izotropija) ili su u dva, odnosno
tri međusobno okomita smjera
različita (ortotropija), ili su pak različita u tri međusobno priklonjena
smjera (anizotropija).
Kod materijala s amorfnom
strukturom diskretne su čestice nepravilno raspoređene u prostoru. Amorfna su tijela
(staklo, guma, smola) izotropna, jer imaju jednaka svojstva u svim smjerovima.
Materijal s polikristalnom
strukturom sastavljen je od velikog broja vrlo sitnih kristala različitih dimenzija i
orijentacije (npr. čelik i drugi metali). Svaki je pojedini kristal u sklopu
ove strukture anizotropan,
ali zbog velikog broja i zbog potpuno nepravilna rasporeda kristala u masi
takav materijal, promatrano u cijelosti ima jednaka svojstva u svim smjerovima,
tj. ponaša se kao izotropni materijal.
Struktura građevnih materijala, međutim,
vrlo je nepravilna i složena i ne postoji građevni materijal kojemu se
struktura može usporediti sa strukturom kristala. Postoje, međutim materijali
koji se sastoje od više sitnih u prostoru
različito orijentiranih kristala (magmatske stijene, metali). Postoje materijali amorfnih struktura i lančanih veza
(staklo, polimeri). No, najviše građevnih materijala (betoni svih vrsta, keramika, drvo, kamen sedimentnog
podrijetla itd.) imaju strukture različite od navedenih tipova, npr.
beton se sastoji od agregata ili ispune i stvrdnutog veziva. Dakako, da se u
njemu mogu naći i kristali i amorfne strukture (geli) i sedimentni ostaci. Tako
sastavljeni betoni trebali bi biti izotropni, a njihova su anizotropna ili
ortrotropna struktura posljedica načina proizvodnje betona, načina ugradnje i zbijanja. Mikroskopske snimke čelika, cementnog
betona, polimera i drva pokazuju kolike razlike postoje u strukturama
građevnog materijala, a da nijedna struktura ne predstavlja jednu od osnovnih struktura. Odstupanja od osnovnih struktura
pojavljuju se i u materijalima koji se upotrebljavaju u ostalim tehničkim
granama. U građevnim materijalima ona su znatno veća, i to je sigurno jedan od razloga da je rasipanje rezultata ispitivanja
građevnih materijala znatno veće. U svakoj od tih struktura ima dijelova
različitih mehaničkih svojstava, različite čvrstoće, tvrdoće i deformabilnosti.
Osim toga, većina je građevnih materijala
šupljikava, a u nekima čak veći dio obujma čine šupljine, koje su međusobno odijeljene tankim stijenkama (npr.
stiropor). Neki materijali imaju te šupljine ispunjene vodom, koja je
tada jedan od elemenata o kojem ovise njihova svojstva.
Karakteristika amorfnih tijela je
izotropnost njihovih svojstava, tj. nezavisnost svojstava od smjera u prostoru. Anizotropija se kod njih javlja samo kao
posljedica vanjskih utjecaja koji uzrokuju da se kristalna zrna ili molekule orjentiraju prvenstveno na određen način, kao
što je to slučaj kod tzv. tekstura, npr. materijala istegnutog u
vlaknastu strukturu. Fizička svojstva kristala mogu biti različita u različitim
smjerovima i to se iskorištava za određivanje simetrije kristala. Ako se
monokristal izbrusi u oblik kugle pa uroni u
tekućinu koja ga otapa, on poprima oblike karakteristične za simetriju danog kristala
jer je brzina otapanja u različitim smjerovima različita. Na temelju simetrije
izjedina nastalih jetkanjem na plohama
kristala može se odrediti deset dvodimenzijskih kristalnih klasa. Transparentni
kristali mogu biti optički izotropni
i anizotropni; izotropni su kristali kubnog sastava, a anizotropni su ili optički jednoosni (tetragonski, heksagonski) ili
optički dvoosni (rompski, monoklinski, triklinski). Petnaest
necentrosimetričnih kristalnih klasa zakreće ravnine polarizacije svjetlosti.
Neki kristali necentrosimetričnih klasa
bivaju električki nabijeni na suprotnim krajevima u smjeru određenih osi simetrije ako im se mijenja temperatura
(piroelektricitet) ili ako su podvrgnuti mehaničkim naprezanjima
(piezoelektricitet). Kristal koji je izotropan u odnosu na neka svojstva, npr.
optička, može pokazivati anizotropiju drugih svojstava, npr. mehaničkih ili
magnetskih. Anizotropna svojstva kristala mogu se karakterizirati tenzorskim
veličinama s to manje nezavisnih komponenata što je više simetrija kristalne
klase kojoj kristal pripada; npr. elastična svojstva se u anizotropnom kristalu
opisuju tenzorom Četvrtog ranga koji za
triklinski sistem ima 21 komponentu, za monoklinski 13, za rompski 9, a za
kubni 3. Anizotropija magnetskih
svojstava osobito je velika kod feromagnetskih kristala, u kojima postoje smjerovi
spontane magnetizacije feromagnetskih domena.
2. Statička ispitivanja
Djelovanjem središnje
vlačne sile najbolje se postiže homogeno naprezanje. Prijenos vlačne sile s kidalice na uzorak
može biti hvataljkama ili čeljustima (metali, sintetski materijali), pužnicima
(užad, kabeli) i pločama koje
se lijepe smolama na uzorak.
Primjenjujući St. Venant-ov princip,
homogeno naprezanje dobiva se u srednjem dijelu uzorka, jer je u okolici mjesta prijenosa sile homogenost poremećena
koncentracijama. Na kidalici je moguće u svakom trenutku utvrditi vrijednost sile, a relativne ili stvarne
deformacije mogu se mjeriti posebnim instrumentima
ili registrirati posebnim uređajem. Obično se na temelju tih podataka sastavlja
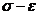 dijagram ili radni dijagram. Ovisno o vrsti
materijala dobivamo slijedeći dijagram:
dijagram ili radni dijagram. Ovisno o vrsti
materijala dobivamo slijedeći dijagram:
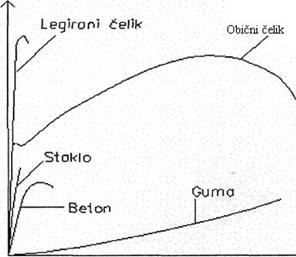
Slika:  dijagram za razne
materijale
dijagram za razne
materijale
2.1. Akustički
postupci
Postupci kojima se
utvrđuju fizička i kemijska svojstva materijala, odnosno kojima se utvrđuje ponašanje materijala i konstrukcija pri
djelovanju naziva se ispitivanje materijala.
Kod bezrazornih
ispitivanja veliku grupu čine postupci u kojima se koristi ultrazvuk. Poznato
je da se u elastičnim
materijalima zvuk širi određenom brzinom, koja npr. u zraku iznosi 330 m/s, a u
čvrstim elastičnim tijelima od 1.5 do 5.0 km/s.
U štapu od materijala
modula elastičnosti E i gustoće 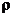 teoretski brzina zvuka
iznosi:
teoretski brzina zvuka
iznosi:
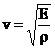
dok je brzina širenja zvuka u neograničenoj elastičnoj sredini:
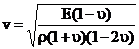
Ako poznajemo 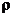 i
i 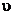 , mjerenjem brzine zvuka v može se odrediti modul
elastičnosti odnosno čvrstoća. Za takva mjerenja služe posebni elektronički
uređaji koji se sastoje od dvije sonde, pobuđivača i prijemnika oscilacija, te
uređaja za mjerenje vremena i osciloskopa na kojemu je moguće promatrati sliku
primljenog zvučnog vala. Sonde se prislone na ispitivani uzorak materijala na
poznati razmak te se mjeri
vrijeme prolaza ultrazvučnih oscilacija od pobuđivača do prijemnika.
Frekvencija tih oscilacija je od 50 do 120
kHz, a odabrana je tako da utrošak energije bude što manji, da disipacija zbog
heterogenosti betona bude u prihvatljivim granicama te da točnost mjerenja
vremena širenja ultrazvuka bude što
veća. Pokazalo se, naime, da je uz te frekvencije oscilacijama obuhvaćen
razmjerno mali dio obujma tijela, te
da se oscilacije šire kao uski snop koji je to uži što je frekvencija viša. Današnji uređaji mogu mjeriti vrijeme od 0,2
, mjerenjem brzine zvuka v može se odrediti modul
elastičnosti odnosno čvrstoća. Za takva mjerenja služe posebni elektronički
uređaji koji se sastoje od dvije sonde, pobuđivača i prijemnika oscilacija, te
uređaja za mjerenje vremena i osciloskopa na kojemu je moguće promatrati sliku
primljenog zvučnog vala. Sonde se prislone na ispitivani uzorak materijala na
poznati razmak te se mjeri
vrijeme prolaza ultrazvučnih oscilacija od pobuđivača do prijemnika.
Frekvencija tih oscilacija je od 50 do 120
kHz, a odabrana je tako da utrošak energije bude što manji, da disipacija zbog
heterogenosti betona bude u prihvatljivim granicama te da točnost mjerenja
vremena širenja ultrazvuka bude što
veća. Pokazalo se, naime, da je uz te frekvencije oscilacijama obuhvaćen
razmjerno mali dio obujma tijela, te
da se oscilacije šire kao uski snop koji je to uži što je frekvencija viša. Današnji uređaji mogu mjeriti vrijeme od 0,2 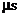 , a najveće su udaljenosti sonda do 8 m. Duljina vala iznosi 3 do 6 cm i ona mora biti veća od najvećih
zrna agregata u betonu, ako se žele na slici vala na osciloskopu izbjeći
nepravilnosti zbog heterogenosti sastava betona. Postoje dvije vrste uređaja za
ispitivanje ultrazvukom:
, a najveće su udaljenosti sonda do 8 m. Duljina vala iznosi 3 do 6 cm i ona mora biti veća od najvećih
zrna agregata u betonu, ako se žele na slici vala na osciloskopu izbjeći
nepravilnosti zbog heterogenosti sastava betona. Postoje dvije vrste uređaja za
ispitivanje ultrazvukom:
-
s neprekinutom pobudom
- s impulsnom pobudom
S uređajima koji neprekidno pobuđuju
uzorak mjeri se brzina prolaska zvuka kroz materijal. Uređaji koji daju kratke ultrazvučne impulse daju
informaciju više o materijalu koji se ispituje. Impulsi se šalju u vremenskim razmacima od 1/20, 1/10 ili 1/5 s, a
na osciloskopu se može registrirati prigušenje čime se dobiva podatak više o ispitivanom materijalu.
Na temelju slike odraza može se utvrditi površinska oštećenja i pukotine
u uzorku materijala koji se ispituje.
2.2. Ispitivanje rezonantnim titranjem
Ispituje se uzorak pravilnog
geometrijskog oblika, najčešće prizmatičnog oblika. Također je moguće odrediti modul
elastičnosti. Rezonantno titranje prizme se pojavljuje kad je vrijeme između
pojedinih impulsa
uzbuđivača jednako vremenu koje je potrebno da val impulsa prođe čitavom
prizmom i da se vrati na
mjesto uzbude. To vrijeme iznosi:
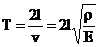
Pošto je frekvencija
f= l/T, slijedi da je modul elastičnosti:
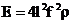
Rezonantna
frekvencija određena je najvećom amplitudom vala primljenog na drugom kraju
prizme (stojni
val). Slično se može dovesti u rezonantno titranje bilo kakav elastičan sustav,
pa se taj postupak primjenjuje
i za određivanje krutosti čitavog sustava za vrijeme savijanja, torzije i
izvijanja, i sl.
2.3. Ispitivanje zračenjem
Rengenskim i gama-zračenjem može se utvrditi homogenost i
gustoća materijala.
Homogenost, prisutnost stranih tvari,
šupljine i drugo mogu se odrediti iz snimke na filmu koji se postavlja na drugoj
strani prozračenog tijela. Moguće prozračiti do 150mm debeli čelik ili do 40cm debeli sloj betona.
Obzirom da su deformacije materijala
izazvane ultrazvukom male, nalazimo se nisko u dijagramu pa je proračunati modul elastičnosti u stvari
dinamički modul elastičnosti.

Slika: 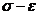 dijagram
dijagram
3. Rezultati
ispitivanja dinamičkog modula elastičnosti
U ovom dijelu seminara prikazat će se
rezultati ispitivanja dinamičkog modula elastičnosti dva različita materijala:
Ø čelik ->
izotropni materijal
Ø drvo ->
anizotropni materijal
3.1. Ispitivanje čelika
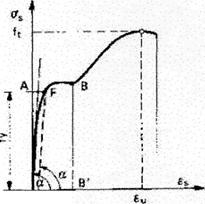
Visokovrijedni čelici
dobiveni legiranjem, a ne obrađivanjem hladnim postupkom, pokazuju ove karakteristike
prirodnih čelika s nešto nižom granicom izduženja 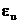 i tako naglašenom
granicom popuštanja.
i tako naglašenom
granicom popuštanja.
3.2. Ispitivanje
drveta
U svrhu građevinskog materijala drvo se primjenjuje od davnina. Danas
pored upotrebe čelika i
betona u graditeljstvu, drvene konstrukcije još uvijek imaju svoje
mjesto.
Prednosti su mu: mala
zapreminska težina, relativno velika čvrstoća paralelno sa vlaknima, laka obrada, mala osjetljivost na temperaturne
promjene i dr.
Drvo ima i svoje
nedostatke. Oni se manifestiraju u : anizotropiji i kvalitetama nastalim
biološkim faktorima (rastom drveta), mogućim greškama u drvetu (truljenje),
podložnost utjecaju gljiva i insekata, zavisnost mehaničkih osobina od vlažnosti,
zapaljivost drveta i rad drveta na zraku (skupljanje i bubrenje).
No unatoč tome drvo
se uspješno nosi sa betonom i čelikom. Čvrstoća drveta (I kvalitetne klase) veća je nego čvrstoća nekih betona.
Slijedeća slika prikazuje odnose dopuštenih napona između drveta i betona za neke slučajeve naprezanja koji uspješno
ilustriraju prethodne tvrdnje.
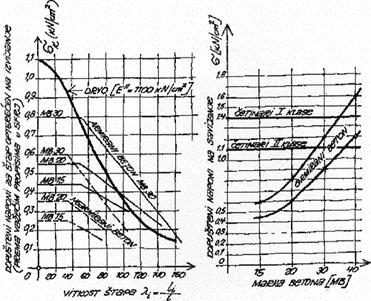
Eksperimentalnim
ispitivanjem pokazana je ovisnost između granične čvrstoće i zapreminske mase drveta.
Dokazano je da širina godova utiče na čvrstoću drveta. Previše uski, a isto
tako i previše široki godovi
smanjuju čvrstoće drveta.
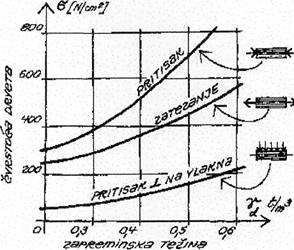
Drvo kao materijal ubraja se u one materijale kod kojih je
otpornost materijala veća ukoliko je prirast opterećenja
brži, odnosno kod veće brzine prirasta opterećenja dobijaju se veće čvrstoće.
Ovo se objašnjava reološkim karakteristikama drveta koje su u uskoj vezi sa
submikroskopskom strukturom zidova elemenata građe drveta.
Isto tako
eksperimentalna ispitivanja su pokazala da ako se serija uzoraka identičnog
oblika optereti različito po vremenu trajanja opterećenja, to onda i lom materijala
nastaje u različitim vremenskim intervalima. Ukoliko je veće opterećenje brže
dolazi do loma materijala. Međutim, ako se to isto veliko opterećenje nanese
trenutno, u vrlo kratkom vremenskom intervalu, dolazi do loma materijala. Kao
što se iz slike vidi dobija
se jedna asimptotska krivulja koja pokazuje da granična čvrstoća drveta pada sa
nanošenjem opterećenja kroz vrijeme. Padanje
čvrstoće teži nekoj konstantnoj veličini 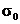 i ta čvrstoća naziva
se otpornost (čvrstoća) drveta na dugotrajno opterećenje ili trajna
čvrstoća. Ispitivanja pokazuju da je
i ta čvrstoća naziva
se otpornost (čvrstoća) drveta na dugotrajno opterećenje ili trajna
čvrstoća. Ispitivanja pokazuju da je 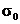 približno oko 60% od
vrijednosti čvrstoće pri slomu od trenutnog opterećenja.
približno oko 60% od
vrijednosti čvrstoće pri slomu od trenutnog opterećenja.
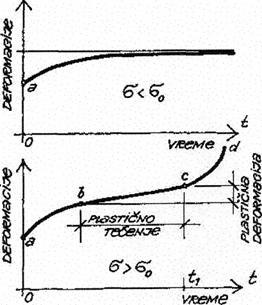
Asimptota na dobivenu krivulju
definira dva područja. U prvom području, kada je 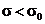 lom materijala ne može
nastupiti i pored dugotrajnog opterećenja. Prilikom nanošenja opterećenja
nastaje trenutna
(početna) deformacija (0-a). Vremenom, deformacije najprije rastu, opterećenje
je konstantno, a potom se gube, odnosno krivulja deformacije kroz vrijeme asimptotski
se približava nekoj granici.
lom materijala ne može
nastupiti i pored dugotrajnog opterećenja. Prilikom nanošenja opterećenja
nastaje trenutna
(početna) deformacija (0-a). Vremenom, deformacije najprije rastu, opterećenje
je konstantno, a potom se gube, odnosno krivulja deformacije kroz vrijeme asimptotski
se približava nekoj granici.
Međutim u području kada je 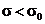 , kada se koristi čvrstoća iznad čvrstoće za dugotrajno
opterećenje
, kada se koristi čvrstoća iznad čvrstoće za dugotrajno
opterećenje 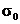 poslije
početne-trenutne-deformacije (0-a) i poslije izvjesnog smanjenja brzine
deformacija, do točke b na dijelu b-c, nastupa prirast deformacija konstantnom brzinom.
Deformacija b-c naziva se plastična deformacija, interval b-c=plastično tečenje
materijala (ili «puzanje» materijala) u vremenu t1. Poslije vremena t1
nastupa ubrzan prirast deformacija koji u točki d dovodi do loma materijala (lom
uslijed «tečenja»
materijala).
poslije
početne-trenutne-deformacije (0-a) i poslije izvjesnog smanjenja brzine
deformacija, do točke b na dijelu b-c, nastupa prirast deformacija konstantnom brzinom.
Deformacija b-c naziva se plastična deformacija, interval b-c=plastično tečenje
materijala (ili «puzanje» materijala) u vremenu t1. Poslije vremena t1
nastupa ubrzan prirast deformacija koji u točki d dovodi do loma materijala (lom
uslijed «tečenja»
materijala).
Znači deformacije mogu imati dvojaki tok:
-poslije određenog vremena teže nekoj
konačnoj-određenoj-vrijednosti koja može imati intezitet od 1,6 do 2-struke vrijednosti od elastičnih
deformacija (pri tome su naponi u dopuštenim granicama)
-pri korištenju povećanih napona,
napona iznad granice dugotrajne čvrstoće, elastične deformacije
superponiraju se sa plastičnim deformacijama, sa deformacijama od plastičnog
tečenja materijala, i u nekom vremenu t dovode do loma.
Dakle drvo kao materijal ima
svojstvo prirasta deformacija kroz vrijeme, kako u elastičnoj tako i u plastičnoj okolini
ponašanja materijala. Drugim riječima, poslije nenošenja opterećenja i
poslije početnog ali konstantnog napona deformacije drveta vremenom rastu.
Drvo vrlo dobro
prenosi učestala, alternativna i kratkotrajna ciklička opterećenja. Dok se kod metala vrlo brzo
pojavljuje zamor materijala, drvo je zbog specifičnih veza molekula celuloze i strukture
submikroskopske građe drveta (mikrofibrila) vrlo otporno na ovu vrstu
opterećenja.
Drvo se smatra
nehomogenim i anizotropnim materijalom zbog svojih različitih svojstava koja pokazuje kod
djelovanja sila iz različitih smjerova. Modul elastičnosti drveta ovisi o vrsti
drveta, strukturi,
volumnoj težini, sadržaju vode, smjera vlakna, temperaturi i obliku presjeka.
Slika
prikazuje glavne osi kod drveta u kojima se pokazuju različita mehanička
svojstva:
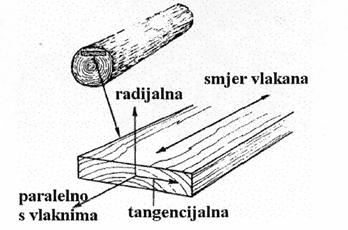
Slika: Glavne osi drveta
Nakon mjerenja brzine
prolaska zvuka kroz drvo dobiveni su slijedeći rezultati:
•
u smjeru vlakna
v = 3200 - 5200 m/s
•
okomito na vlakna v = 900 - 1500 m/s
Modul elastičnosti
drveta je u smjeru vlakana (E1) najveći; njegova prosječna
vrijednost kreće se od 300 do 2500 kN/cm2. Modul elastičnosti okomito
na vlakna u radijalnoj ravnini kreće se u granicama Er= 1/6
... 1/23 E1, a modul elastičnosti okomito na vlakna u tangentnoj
ravnini kreće se u granicama Et=l/23...1/40E1.
Najbolje je istražen
modul elastičnosti drva u smjeru vlakana. Ostale elastične konstante za tri osi
simetrije istražene su samo
za neke vrste drva.
Slijedeća slika
prikazuje rezultate ispitivanja uzorka borovine na tlak i vlak. I kod vlačnog i
tlačnog ispitivanja
pojavljuje se znatna razlika između ishodišnih modula elastičnosti što
potvrđuje anizotropna svojstva drveta bez obzira na karakter naprezanja.
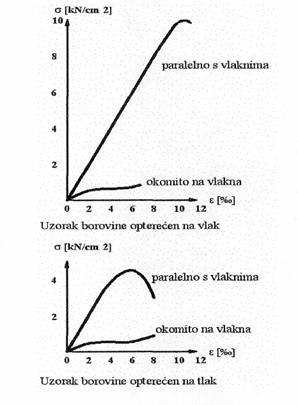
Kada vlačna sila djeluje
paralelno sa vlaknima koristi se čvrstoća drveta na vlak. Dakle vlačna sila prenosi se direktno preko vlakana. Iz ovog
razloga nepravilnosti građe drveta, posebno kvrgavost,
mogu u mnogome umanjiti vlačnu čvrstoću drveta paralelno sa vlaknima (čak i za
50 - 80%).
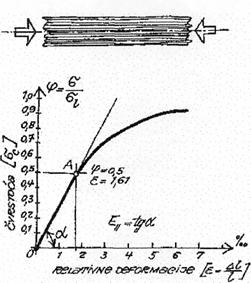
Rad drveta
na vlak paralelno vlaknima najbolje se vidi na slijedećem dijagramu:
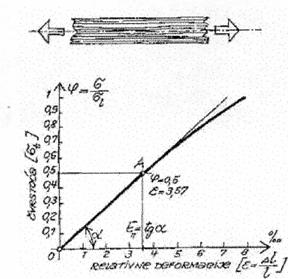
Ovaj dijagram se dobija ako se na os
apscise nanesu relativne deformacije u 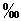 , a na ordinati odnos (
, a na ordinati odnos (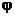 ) čvrstoće na vlak izražen u dijelovima čvrstoće do sloma. Iz
slike se vidi da od nula do točke A (
) čvrstoće na vlak izražen u dijelovima čvrstoće do sloma. Iz
slike se vidi da od nula do točke A (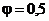 i
i 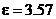
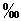 ) je prava linija. Točka
A naziva se granica proporcionalnosti. I dalje, poslije točke A krivulja neznatno odstupa od prave linije. Vidi se
da lom materijala nastupa trenutno, bez prethodnog naglog povećanja
deformacija, što je karakteristično drvetu kao materijalu.
) je prava linija. Točka
A naziva se granica proporcionalnosti. I dalje, poslije točke A krivulja neznatno odstupa od prave linije. Vidi se
da lom materijala nastupa trenutno, bez prethodnog naglog povećanja
deformacija, što je karakteristično drvetu kao materijalu.
Kada vlačna sila
djeluje uspravno na pravac vlakana koristi se vlačna čvrstoća uspravno na
vlakna. Zbog prirode i
anizotropije materijala granična vlačna čvrstoća drveta okomito na vlakna je za
20 do 25 puta manja od odgovarajuće vlačne
čvrstoće paralelno vlaknima. Prilikom laboratorijskih ispitivanja konstatirana
je vlačna čvrstoća okomito na vlakna u granicama od 150 do 400 N/cm2.
Zbog mogućih grešaka u drvetu vrijednost se može smanjiti do nule.
Kod drva izloženog tlačnoj
sili paralelno vlaknima koristi se tlačna čvrstoća drveta paralelno vlaknima. Elastična
svojstva drveta na tlak paralelno vlaknima slična su kao i vlačna paralelno vlaknima. Na slici je
data krivulja za borovinu do granice proporcionalnosti (točke A) pa sve do
sloma materijala
krivulja je izraženija nego u prethodnom slučaju. Modul elastičnosti paralelno
vlaknima varira
od 106 do 1,8x106 N/cm2. Izvedena ispitivanja
su pokazala da je granična čvrstoća na tlak paralelna s vlaknima i do 2,5
puta manja od čvrstoće na vlak paralelne s vlaknima.
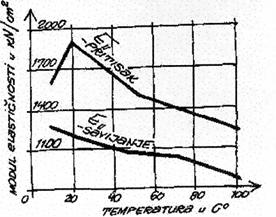
Slijedeća slika prikazuje ovisnost između
neke čvrstoće drveta i temperature odnosno prema modulu elastičnosti. Iz dijagrama je vidljivo da se od 100 °C čvrstoća na tlak i
savijanje smanjuju za oko 50% (od
granične čvrstoće), dok se čvrstoća na vlak smanjuje svega oko 10%. Slične
promjene dešavaju se i s modulom
elastičnosti.
3.3. Ispitivanje betona
Pri naprezanju beton se deformira prema eksponencijalnom zakonu:
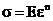
gdje je 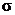 napon, E modul
elastičnosti,
napon, E modul
elastičnosti, 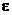 specifično
deponiranje, n eksponent veći od 1.
specifično
deponiranje, n eksponent veći od 1.
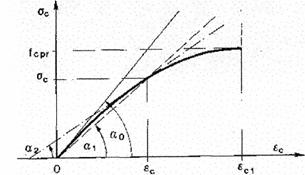
Modul elastičnosti
mjenja se ovisno o naprezanju. Najveći modul betona E0 odgovara neopterećenom materijalu. Ovaj je modul inače
identičan sa tzv. dinamičkim modulom koji se dobiva kada se materijal
napreže do 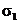 pa se onda rastereti
do
pa se onda rastereti
do 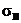 , pri čemu se stvara petlja histereze; ako se taj postupak ponavlja
više puta, linija rada u dijagramu se stabilizira u vidu usko spljoštenog
prstena. Spojnica
dijagonalno suprotnih točaka tog prstena zatvara sa osi apscise kut
, pri čemu se stvara petlja histereze; ako se taj postupak ponavlja
više puta, linija rada u dijagramu se stabilizira u vidu usko spljoštenog
prstena. Spojnica
dijagonalno suprotnih točaka tog prstena zatvara sa osi apscise kut 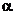 koji je po veličini identičan kutu
koji je po veličini identičan kutu 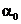 . Tangens ovog kuta daje E0 odnosno Edin.
. Tangens ovog kuta daje E0 odnosno Edin.
Prema našim propisima, u statičkim
proračunima se uzima da je modul elastičnosti stalan, veličine E=210.000 N/mm2,
što odgovara jednoj desetini modula elastičnosti čelika. Druge zemlje propisuju
različite odnose modula elastičnosti čelika i betona, uglavnom između 8 i 15;
ponegdje se predviđaju i promjenjivi moduli; zavisni od prirode opterećenja.
Stvarno se modul elastičnosti teškog betona
za konstrukcije kreće od ~140.000 do ~500.000 N/mm2, zavisno od
kvalitete. Laki betoni imaju znatno manji modul, sve do približno 5.000 N/mm2.
Modul elastičnosti
se povećava kada se prilikom izrade betona primjenjuju pravila izrade što
boljeg betona, dakle: ispravan granulometrijski sastav, čisti agregat, mali
vodocementni faktor, povoljan oblik zrna. Viši modul elastičnosti kamena agregata
utječe povoljno na visinu modula elastičnosti betona. Modul elastičnosti povećava se sa starošću betona.
Navedeni podaci o veličini modula elastičnosti odnose se na
modul kao osobinu materijala napregnutog na pritisak. Modul elastičnosti pri
zatezanju znatno je manji od prethodno navedenog. Sasvim približno može se pretpostaviti da modul elastičnosti na
zatezanje iznosi 0,8 analognog modula na pritisak. Iznalaženje modula
elastičnosti postavlja se kao bitno u mnogim slučajevima u praksi, naročito
prilikom ispitivanja konstrukcija i
preračunavanja napona na osnovu deformacija. U tom slučaju treba raditi sa
stvarnim, a ne sa pretpostavljenim modulom. Ispitivanje i utvrđivanje veličine
modula elastičnosti vrši se u
laboratorijima opterećivanjem probnih uzoraka (prizmi, cilindara) u
istraživačkoj mašini, u granicama
dopuštenih napona, i mjerenjem deformacija (tenzometrima, aparatima sa
zrcalima, trakama za mjerenje i dr.).
U tom cilju uzorci se mašinskim bušenjem vade iz konstrukcije, ili se, pak,
rade specijalne epruvete. Novije
metode kojima se putem vibracija pronalazi dinamički modul elastičnosti
(ultrazvuk, električna analiza, visokofrekventni pulzatori i dr.)
omogućuju postupak bilo u laboratoriju bilo
i na terenu. Veličina dinamičkog modula elastičnosti redovno je veća od one
koja se dobiva statičkim postupcima.
Tehnički problemi u vezi sa
utvrđivanjem stvarnog modula elastičnosti dovele su do stvaranja empirijskih obrazaca namjenjenih
proračunavanju modula iz čvrstoće betona. Najpoznatiji između njih, obrazac švicarskog zavoda EMPA, glasi u nešto
modificiranom obliku:
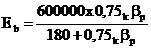
gdje je 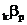 čvrstoća betonske
kocke.
čvrstoća betonske
kocke.
Za marke betona 160 i više, sa uspjehom se
kod nas primjenjuje i formula:
E=150000 + 400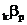 , koji
daje nešto niže vrijednosti od ranije navedenog.
, koji
daje nešto niže vrijednosti od ranije navedenog.
Na veličinu modula
elastičnosti i čvrstoću betona imaju zajedničkog utjecaja samo neki čimbenici: granulometrijski
sastav, količina cementa, ugradba i njega betona i čvrstoće betona imaju samo
opći značaj.
Podjela betona
obzirom na v (ultrazvučna ispitivanja):
|
v (m/s)
|
kvaliteta betona
|
|
<1600
|
vrlo slab
|
|
1600-2000
|
slab
|
|
2000-2800
|
zadovoljavajući
|
|
2800-3600
|
dobar
|
|
3600-4400
|
vrlo kvalitetan
|
4. Optički anizotropni
materijali
Ako svjetlo kroz neki prozirni materijal prolazi u svim smjerovima
jednakim brzinama, materijal je optički
izotropan. Ako brzina širenja ovisi o smjeru, materijal je optički
anizotropan ili dvoloman. Optička anizotropnost opisuje se pomoću
elipsoida indeksa loma. Svaki anizotropni materijal ima tri glavna indeksa, loma n1, n2,
n3 (analogno glavnim naprezanjima 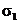 ,
, 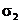 ,
, 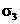 ).
).
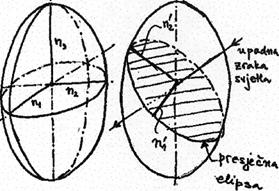
Indeksi loma ujedno su poluosi
elipsoida loma. Kad svjetlo dođe do anizotropnog materijala, treba u mislima
konstruirati elipsoid indeksa loma i presjeći ga ravninom koja je okomita na
upadnu
zraku. Ova ravnina siječe elipsoid u presječenoj elipsi. Poluosi ove
elipse jesu sekundarni glavni indeksi loma 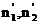 .
.
Upadna zraka rastavlja se na dvije
ravninski polarizirane komponente od kojih jedna titra u pravcu jedne poluosi
presječene elipse, a druga u pravcu druge poluosi elipse. Ove dvije komponente
prolaze
kroz materijal
različitim brzinama v1, v2 koje odgovaraju sekundarnim
indeksima loma, tj.:
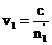 i
i 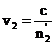
Nakon izlaska iz materijala ove komponente
razlikuju se u fazi koja ovisi o prijeđenom putu u materijalu.
4.1. Fotoelastični
materijali, piezo-optički efekt
Materijali koji su u
nenapregnutom stanju optički izotropni, a kad se nategnu postaju optički anizotropni, pogodni
su za primjenu u fotoelastisimetriji pa se nazivaju fotoelastični materijali. U
ovu grupu materijala spadaju
mnogi polimerni materijali kao: epoksidne smole, polikarbonati, poliesteri
itd., ali
i obično staklo. Međutim, fotoelastičnost stakla je mnogo manja, a i obrada je
teška pa se ne koristi u fotoelastisimetriji.
Pojava optičke anizotropnosti pod opterećenjem naziva se
piezooptički efekt. Za njega vrijedi slijedeći zakon:
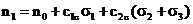
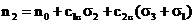
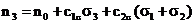
gdje je n0 indeks loma materijala u neopterećenom
stanju, n1, n2, n3 su glavni indeksi loma
materijala u opterećenom stanju, a 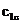 i
i 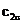 piezo-optičke
konstante materijala. Osi elipsoida indeksa loma paralelne su glavnim naprezanjima.
piezo-optičke
konstante materijala. Osi elipsoida indeksa loma paralelne su glavnim naprezanjima.
Popis literature:
![]() dijagram ili radni dijagram. Ovisno o vrsti
materijala dobivamo slijedeći dijagram:
dijagram ili radni dijagram. Ovisno o vrsti
materijala dobivamo slijedeći dijagram:
![]() dijagram za razne
materijale
dijagram za razne
materijale![]() teoretski brzina zvuka
iznosi:
teoretski brzina zvuka
iznosi:![]()
![]()
![]() i
i ![]() , mjerenjem brzine zvuka v može se odrediti modul
elastičnosti odnosno čvrstoća. Za takva mjerenja služe posebni elektronički
uređaji koji se sastoje od dvije sonde, pobuđivača i prijemnika oscilacija, te
uređaja za mjerenje vremena i osciloskopa na kojemu je moguće promatrati sliku
primljenog zvučnog vala. Sonde se prislone na ispitivani uzorak materijala na
poznati razmak te se mjeri
vrijeme prolaza ultrazvučnih oscilacija od pobuđivača do prijemnika.
Frekvencija tih oscilacija je od 50 do 120
kHz, a odabrana je tako da utrošak energije bude što manji, da disipacija zbog
heterogenosti betona bude u prihvatljivim granicama te da točnost mjerenja
vremena širenja ultrazvuka bude što
veća. Pokazalo se, naime, da je uz te frekvencije oscilacijama obuhvaćen
razmjerno mali dio obujma tijela, te
da se oscilacije šire kao uski snop koji je to uži što je frekvencija viša. Današnji uređaji mogu mjeriti vrijeme od 0,2
, mjerenjem brzine zvuka v može se odrediti modul
elastičnosti odnosno čvrstoća. Za takva mjerenja služe posebni elektronički
uređaji koji se sastoje od dvije sonde, pobuđivača i prijemnika oscilacija, te
uređaja za mjerenje vremena i osciloskopa na kojemu je moguće promatrati sliku
primljenog zvučnog vala. Sonde se prislone na ispitivani uzorak materijala na
poznati razmak te se mjeri
vrijeme prolaza ultrazvučnih oscilacija od pobuđivača do prijemnika.
Frekvencija tih oscilacija je od 50 do 120
kHz, a odabrana je tako da utrošak energije bude što manji, da disipacija zbog
heterogenosti betona bude u prihvatljivim granicama te da točnost mjerenja
vremena širenja ultrazvuka bude što
veća. Pokazalo se, naime, da je uz te frekvencije oscilacijama obuhvaćen
razmjerno mali dio obujma tijela, te
da se oscilacije šire kao uski snop koji je to uži što je frekvencija viša. Današnji uređaji mogu mjeriti vrijeme od 0,2 ![]() , a najveće su udaljenosti sonda do 8 m. Duljina vala iznosi 3 do 6 cm i ona mora biti veća od najvećih
zrna agregata u betonu, ako se žele na slici vala na osciloskopu izbjeći
nepravilnosti zbog heterogenosti sastava betona. Postoje dvije vrste uređaja za
ispitivanje ultrazvukom:
, a najveće su udaljenosti sonda do 8 m. Duljina vala iznosi 3 do 6 cm i ona mora biti veća od najvećih
zrna agregata u betonu, ako se žele na slici vala na osciloskopu izbjeći
nepravilnosti zbog heterogenosti sastava betona. Postoje dvije vrste uređaja za
ispitivanje ultrazvukom:![]()
![]()

![]() dijagram
dijagram