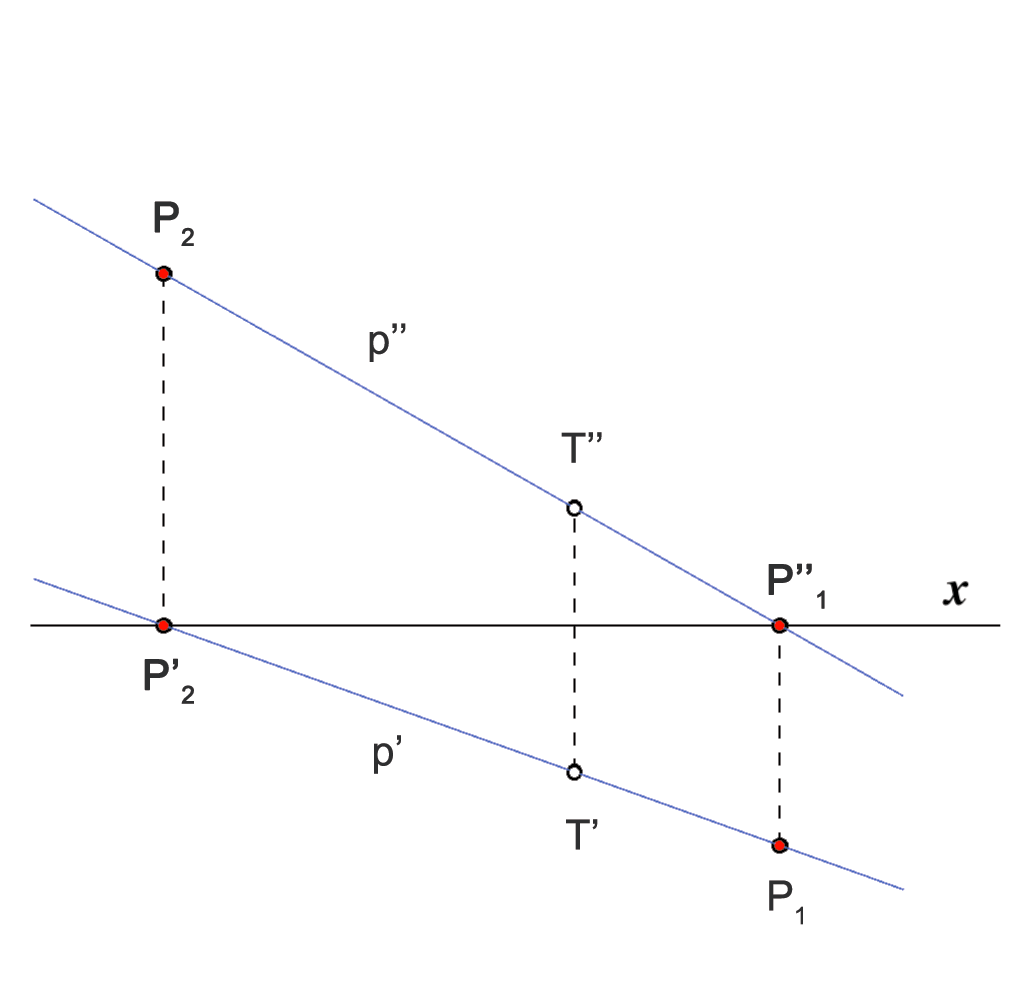
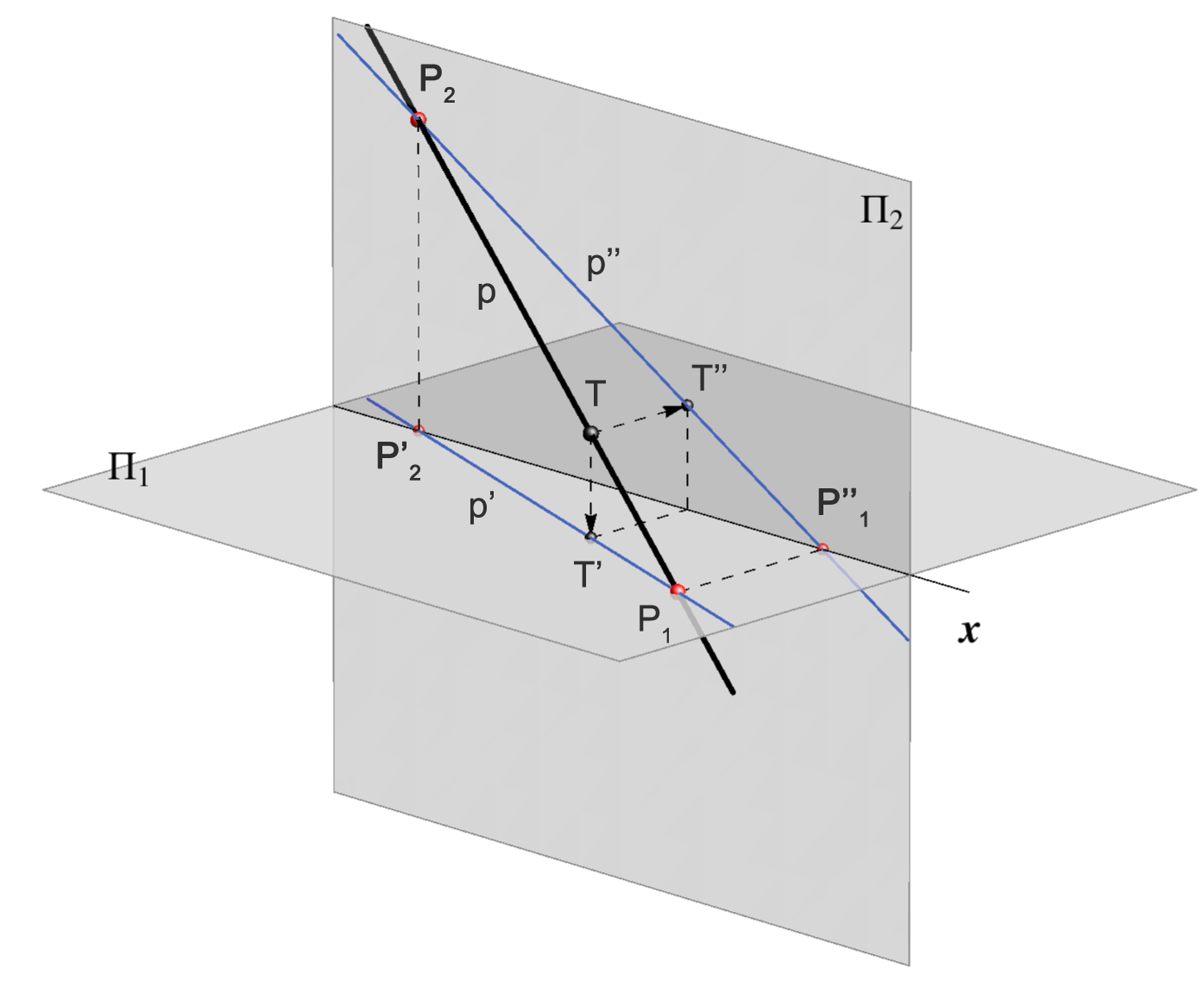
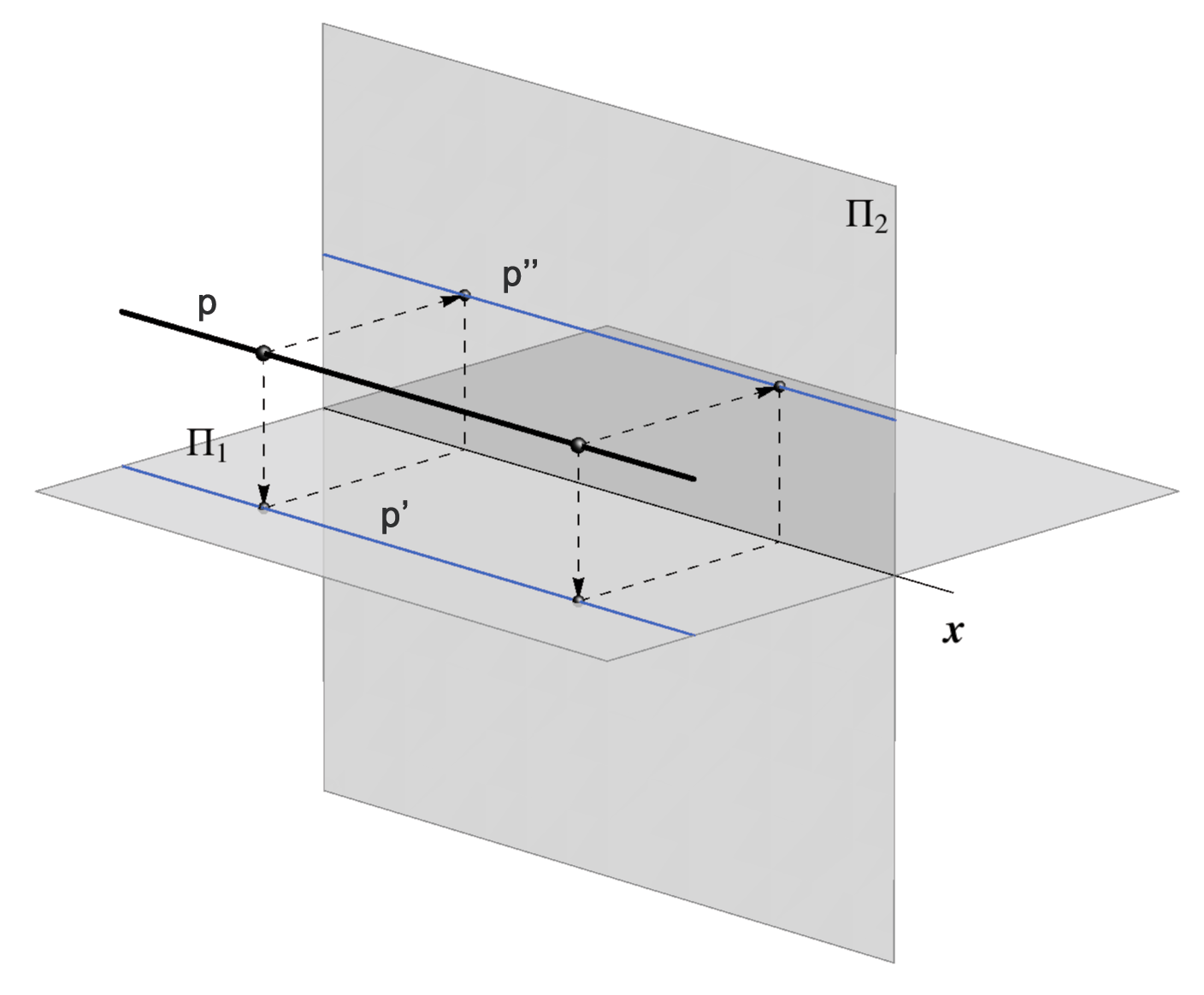
Ako pravac \(\small p\) nije zraka projiciranja (u Mongeovom projiciranju zrake su okomite na ravnine projekcije) njegov su tlocrt i nacrt pravci \(\small p'\) i \(\small p''\). Dakle, u Mongeovoj projekciji pravac prikazujemo parom njegovih projekcija \(\small (p',p'')\).

Ako točka \(\small T\) leži na pravcu \(\small p\), tada njezin tlocrt leži na tlocrtu, a nacrt na nacrtu pravca \(\small p\), odnosno \(\small T\in p\Longrightarrow T'\in p'\,\,\land \,\,T''\in p''\).

Za sve pravce koji nisu okomiti na os \(\small x\) vrijedi i obrat, odnosno \(\small \neg (p\perp x)\, \land\, \small T'\in p'\,\,\land \,\,T''\in p'' \Longrightarrow T\in p\).

Točku \(\small P_1\) u kojoj pravac \(\small p\) probada 1. ravninu projekcije nazivamo prvim probodištem pravca \(\small p\), \(\small P_1= p \cap\Pi_1\).

Točku \(\small P_2\) u kojoj pravac \(\small p\) probada 2. ravninu projekcije nazivamo drugim probodištem pravca \(\small p\), \(\small P_2= p \cap\Pi_2\).

Slika 83
Slika 84

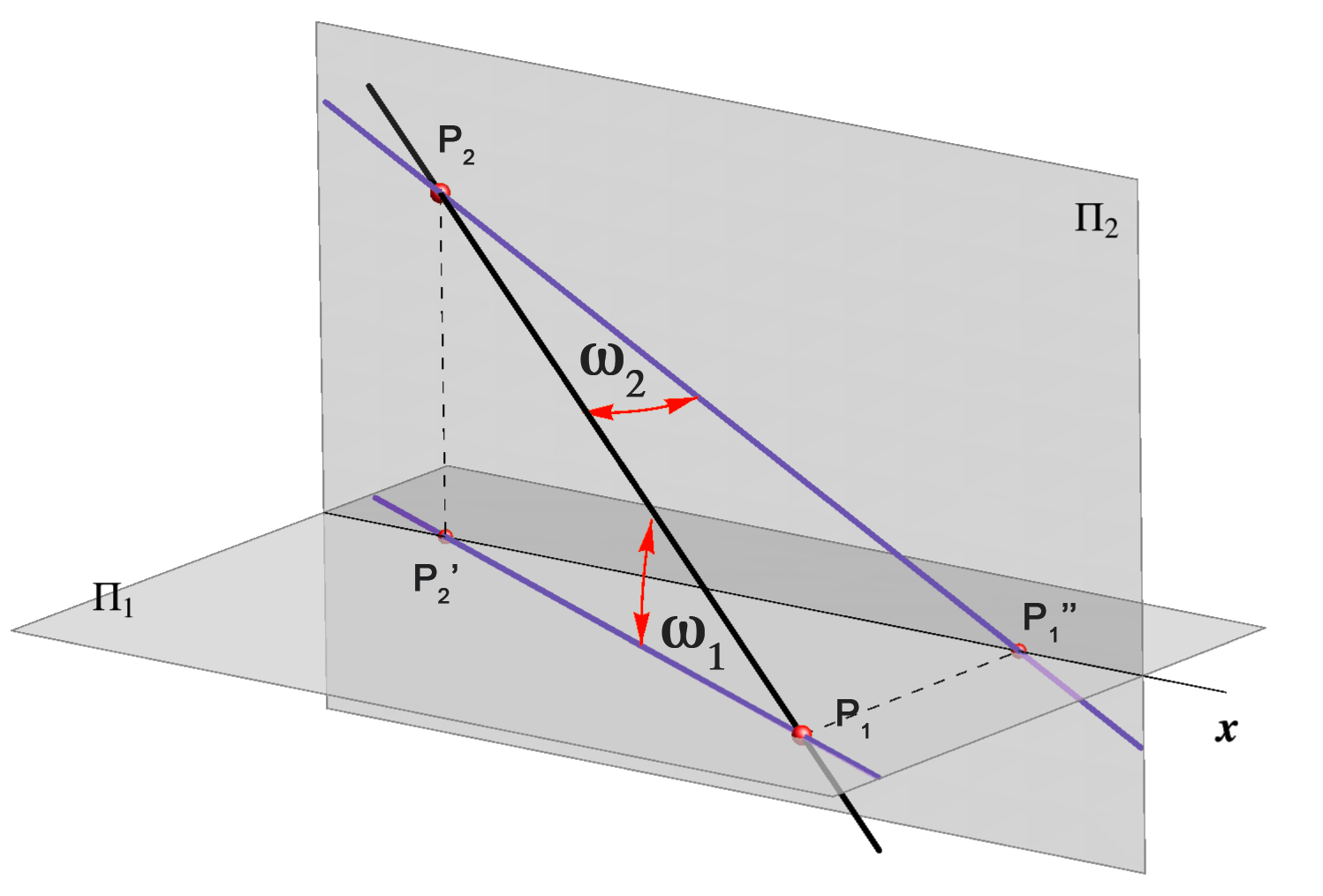
Prvi i drugi prikloni kut pravca

  • Prvi prikloni kut \(\small\omega_1\) nekog pravca \(\small p\) je kut koji taj pravac zatvara s ravninom tlocrta \(\small\Pi_1\). Prema definiciji kuta između pravca i ravnine, to je kut između pravca \(\small p\) i njegovog tlocrta, dakle \(\small \omega_1=\angle (p,p')\).
  • Drugi prikloni kut \(\small\omega_2\) nekog pravca \(\small p\) je kut koji taj pravac zatvara s ravninom nacrta \(\small\Pi_2\), dakle \(\small \omega_2=\angle (p,p'')\).
Slika 85

Posebni položaji pravca

  • Ako je pravac paralelan s ravninom \(\small \Pi_1\), tada su sve njegove točke jednako udaljene od te ravnine, odnosno imaju istu \(\small z\)-koordinatu.

Stoga je nacrt tog pravca paralelan s osi \(\small x\). Budući da vrijedi i obrat, možemo pisati: \(\small p\parallel\Pi_1\Longleftrightarrow p''\parallel x\).

Takav pravac ima u konačnosti samo drugo probodište.

Slika 86
Slika 87: Pravac koji je paralelan s ravninom \(\small\Pi_1\) u nacrtu se projicira paralelno s osi \(\small x\)

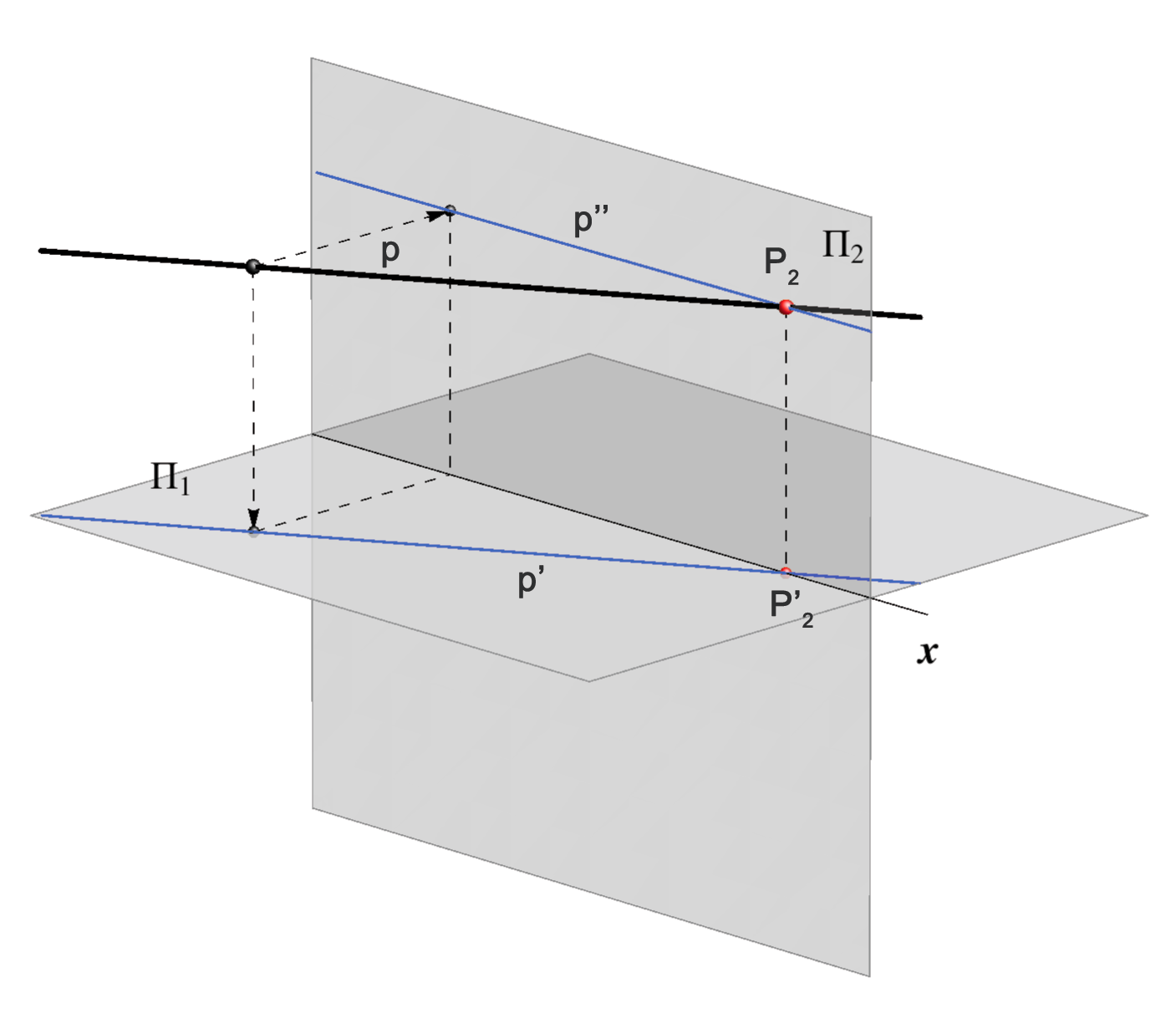
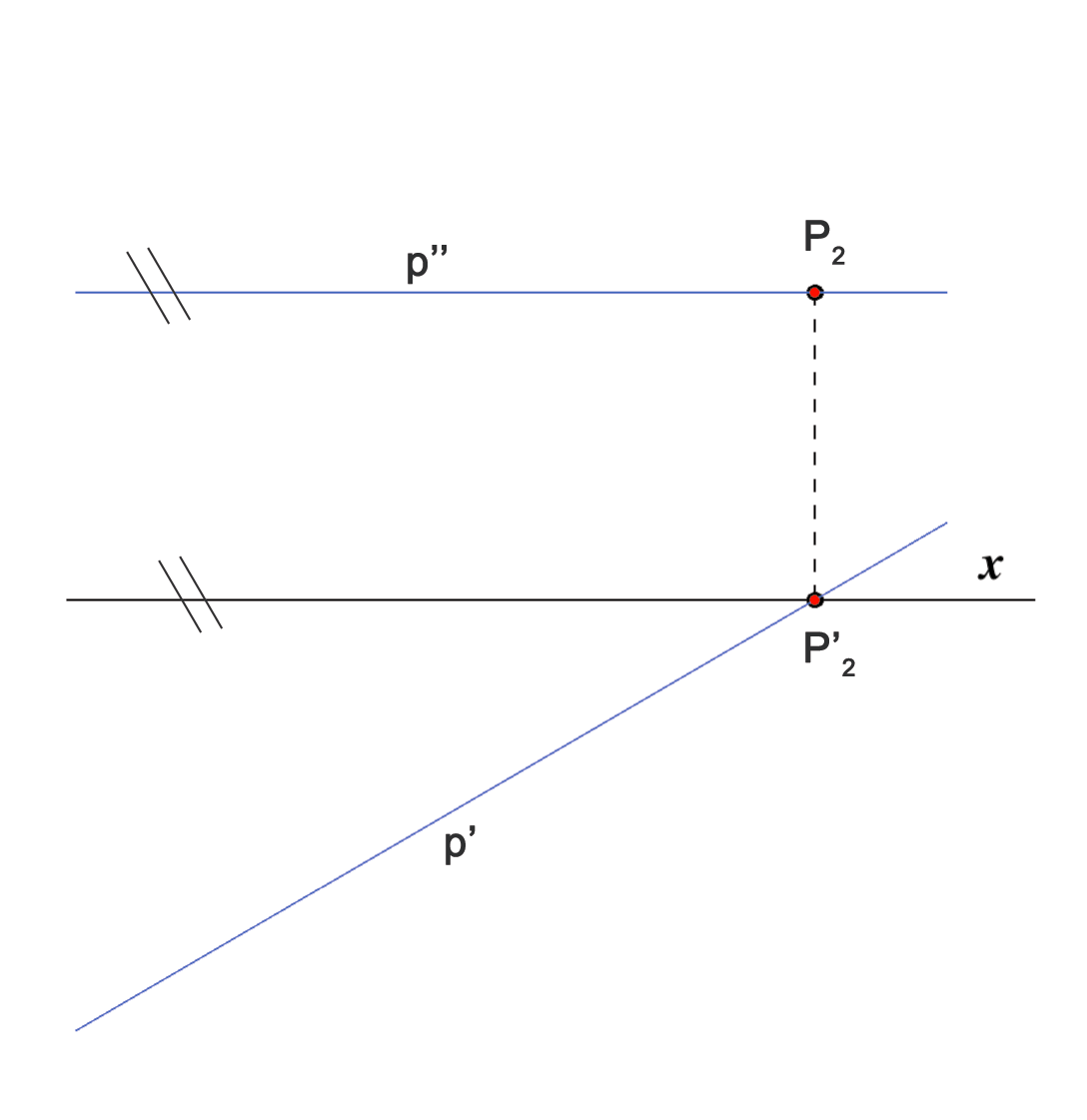
  • Ako je pravac paralelan s ravninom \(\small\Pi_2\), tada su sve njegove točke jednako udaljene od te ravnine, odnosno imaju istu \(\small y\)-koordinatu.

Stoga je tlocrt tog pravca paralelan s osi \(\small x\). Vrijedi i obrat, pa pišemo: \(\small p\parallel\Pi_2\Longleftrightarrow p'\parallel x\).

Takav pravac ima u konačnosti samo prvo probodište.

Slika 88
Slika 89: Pravac koji je paralelan s ravninom \(\small\Pi_2\) u tlocrtu se projicira paralelno s osi \(\small x\)
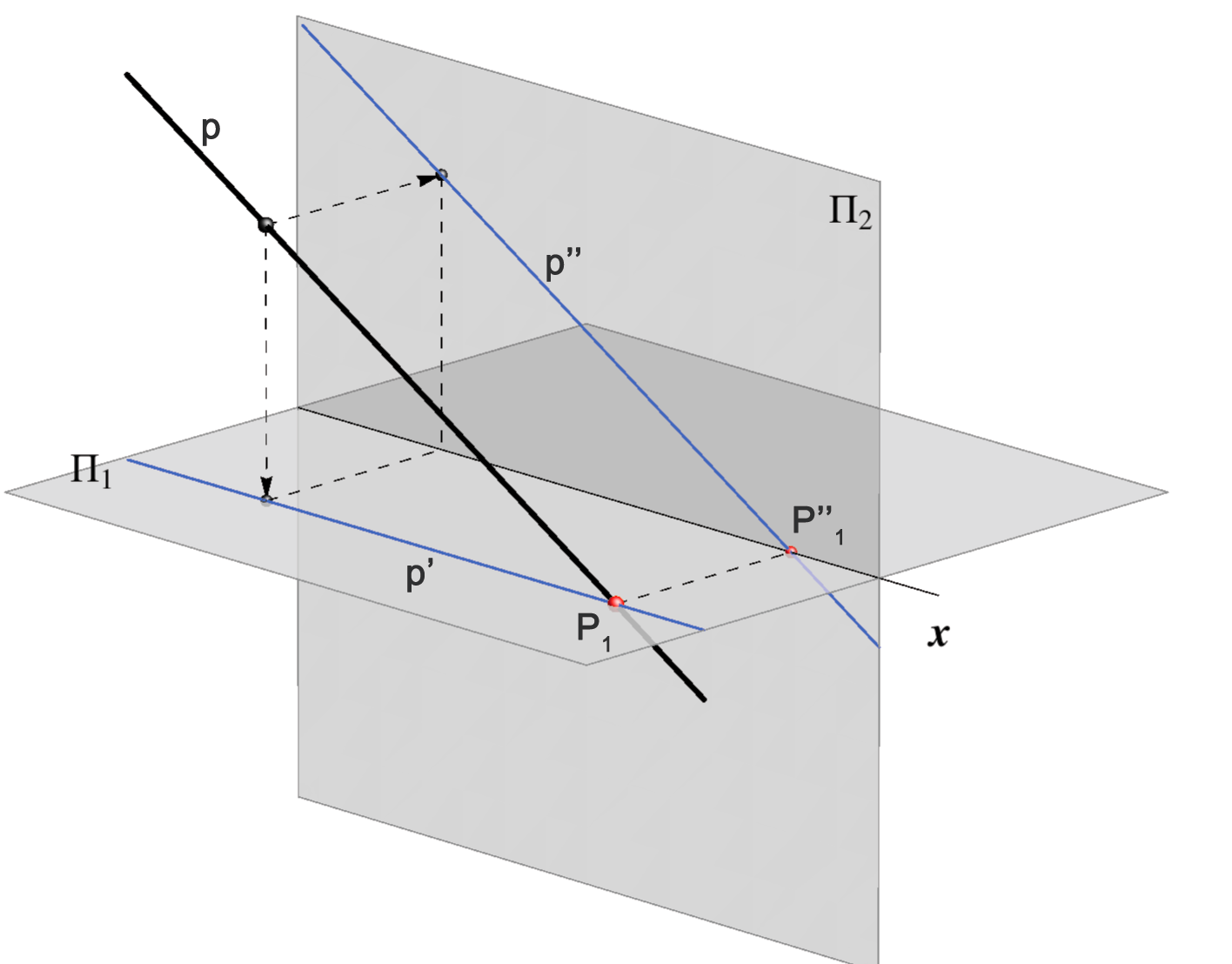
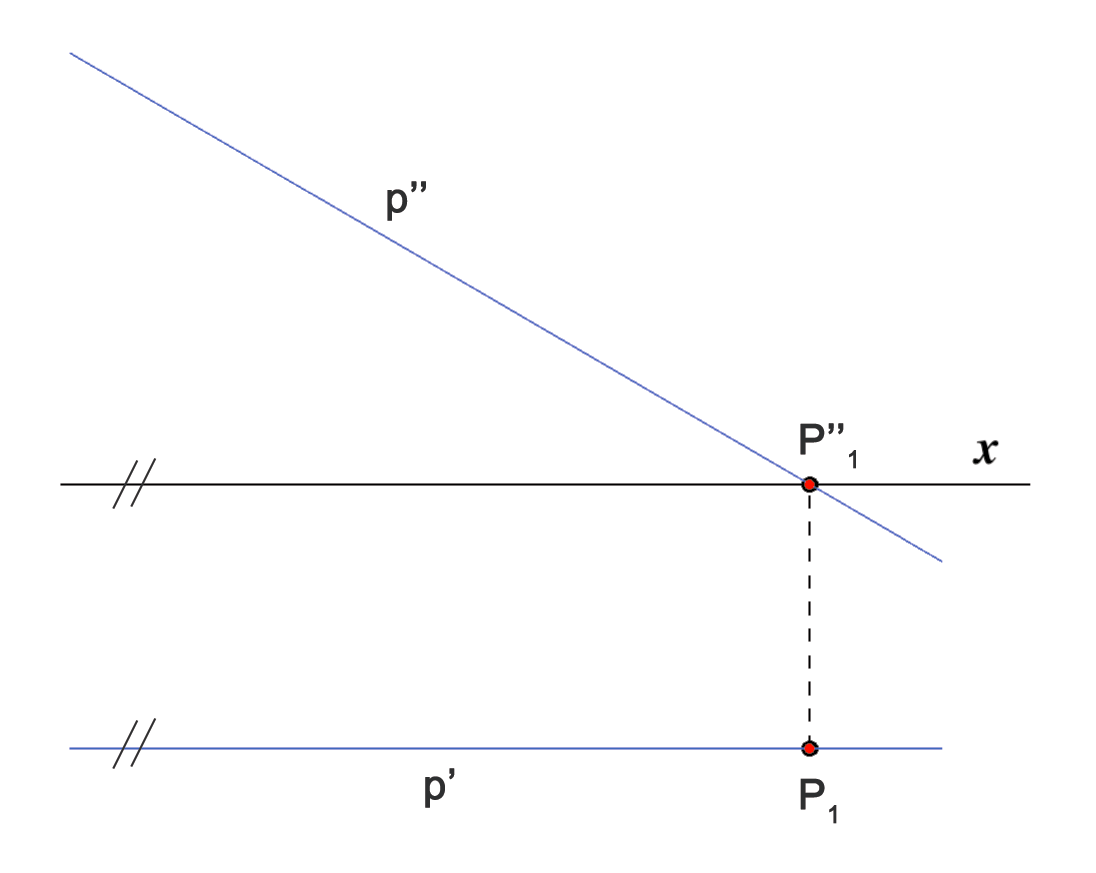
  • Ako pravac leži u ravnini \(\small \Pi_1\) (\(\small\Pi_2\)), tada se nacrt (tlocrt) tog pravca podudara s osi \(\small x\). Vrijedi i obratno.
  • Ako je pravac paralelan s osi \(\small x\), onda su mu i tlocrt i nacrt paralelni s \(\small x\). Vrijedi i obratno.
Slika 90
Slika 91: Pravac koji je paralelan s osi \(\small x\) projicira je u tlocrtu i nacrtu paraleno s osi \(\small x\)
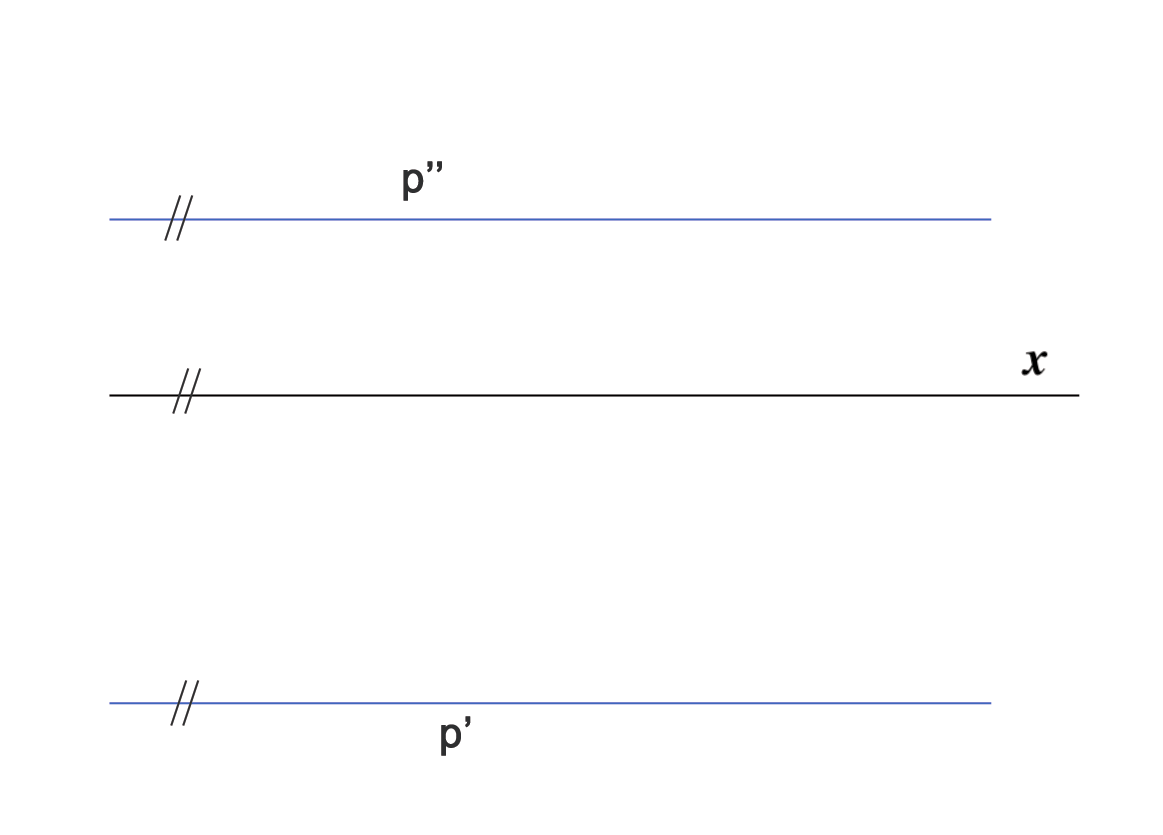
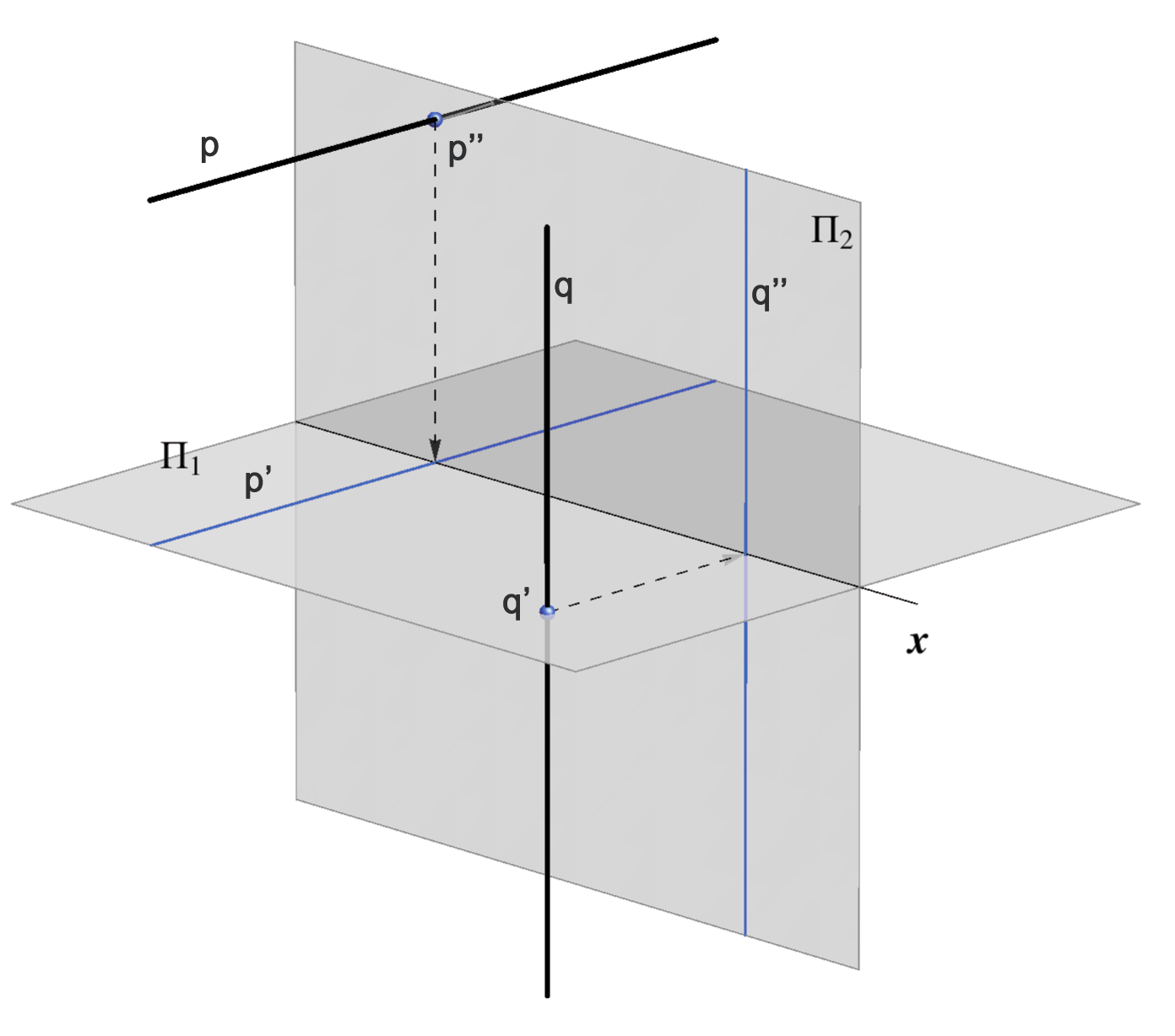
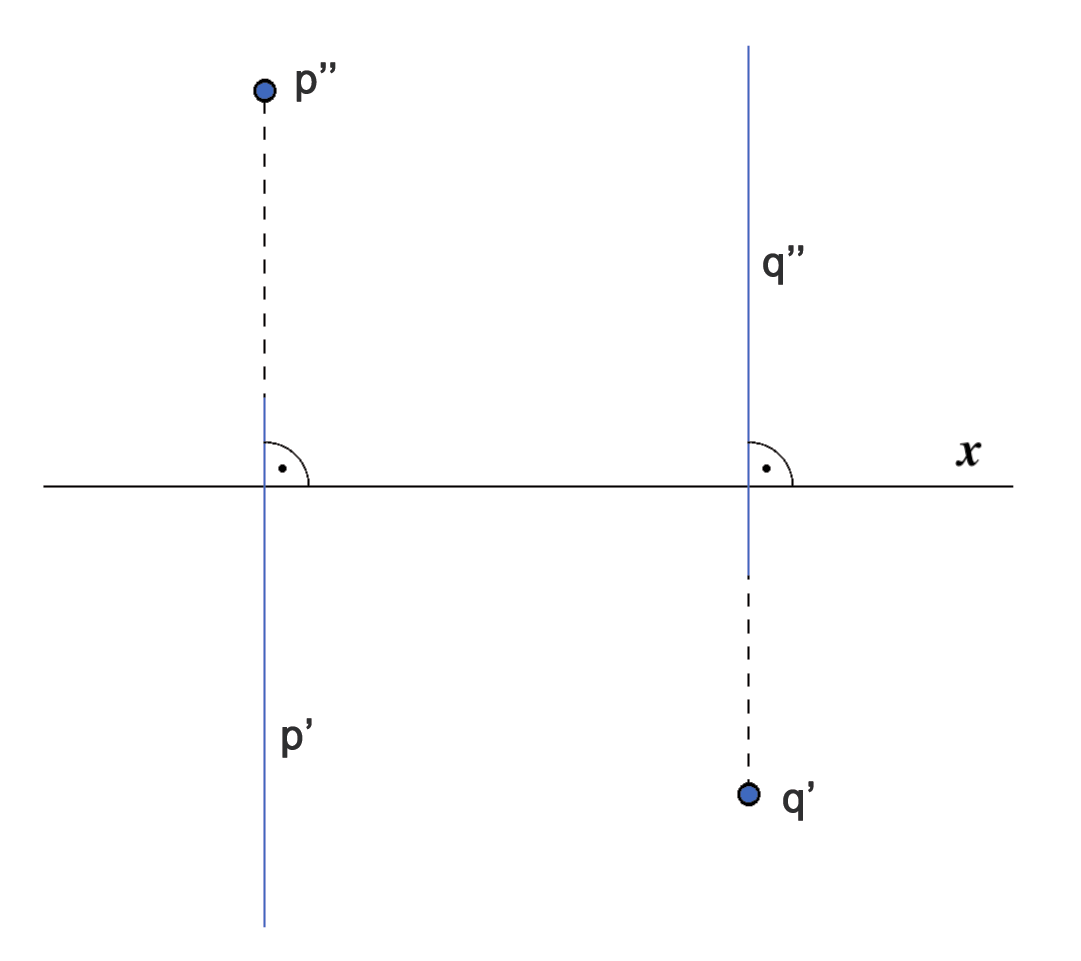
  • Ako je pravac okomit na ravninu \(\small \Pi_1\), tada je njegov tlocrt jedna točka, a nacrt mu je okomit na os \(\small x\).
  • Ako je pravac okomit na ravninu \(\small\Pi_2\), tada je njegov nacrt jedna točka, a tlocrt mu je okomit na os \(\small x\).
Slika 92
Slika 93: Pravci koji su okomiti na ravnine projekcije imaju za jednu projekciju točku

Dva pravca

  • Ako su pravci \(\small a\) i \(\small b\) paralelni, tada su paralelne i njihove odgovarajuće projekcije, odnosno \(\small a\parallel b\Longrightarrow a'\parallel b'\, \land \,a''\parallel b''\).
    Obrat vrijedi za sve slučajeve osim kad su pravci \(\small a\) i \(\small b\) okomiti na os \(\small x\).
  • Ako se pravci \(\small a\) i \(\small b\) sijeku, tada sjecište njihovih tlocrta i sjecište njihovih nacrta leže na istoj ordinali. Vrijedi i obratno. \(^*\)
  • Ako su pravci \(\small a\) i \(\small b\) mimosmjerni, tada sjecište njihovih tlocrta i sjecište njihovih nacrta ne leže na istoj ordinali. Vrijedi i obratno. \(^*\)
Slika 94: Pravci \(\small a\) i \(\small b\) su paralelni
Slika 95: Pravci \(\small a\) i \(\small b\) su ukršteni
Slika 96: Pravci \(\small a\) i \(\small b\) su mimosmjerni

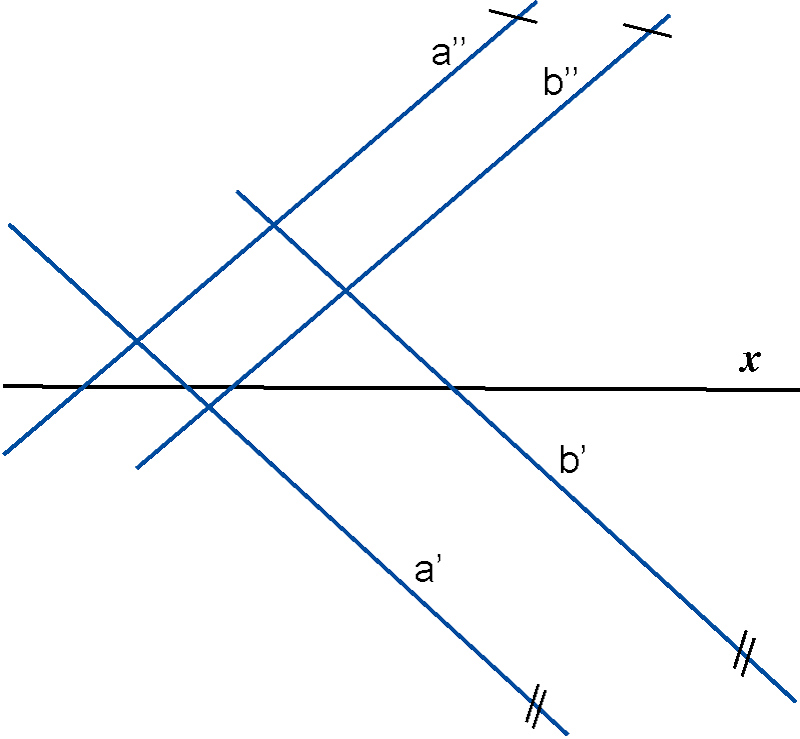
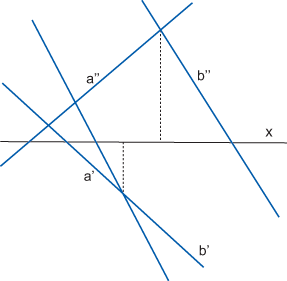
\(^*\) Ove se tvrdnje ne odnose na slučajeve kada se projekcije pravca podudaraju s ordinalom, odnosno kada je pravac okomit na os \(\small x\).

Pravac i ravnine simetrije i koincidencije

Na temelju svojstava što ih imaju projekcije točaka koje leže u ravninama simetrije i koincidencije, za zadani je pravac \(\small p (p',p'')\) vrlo jednostavno konstruirati projekcije njegovih probodišta s tim ravninama.

Ta je konstrukcija dana na slici 97.

  • Ako pravac leži u ravnini simetrije, tada su njegov tlocrt i nacrt simetrični s obzirom na os \(\small x\).
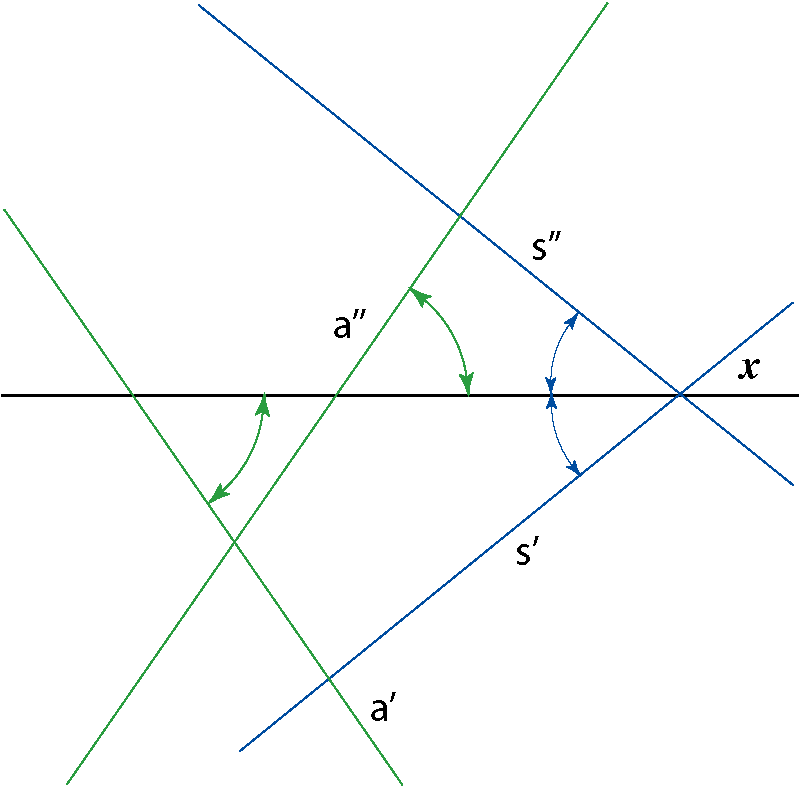
  • Ako je pravac paralelan s ravninom simetrije, tada njegov tlocrt i nacrt zatvaraju jednake kutove (suprotno orijentirane) s osi \(\small x\).
  • Ako pravac leži u ravnini koincidencije, tada se njegov tlocrt i nacrt podudaraju.
  • Ako je pravac paralelan s ravninom koincidencije, tada su njegov tlocrt i nacrt paralelni.

Slika 97: \(\small S = p \cap\Sigma,\,\, K =p \cap\mathrm K\)
Slika 98: \(\small s\subset\Sigma,\,\, a\parallel\Sigma\)
Slika 99: \(\small k\subset\mathrm K,\,\, b\parallel\mathrm K\)