PONOVITE osnovne definicije i teoreme vezane za okomitost.

Ortogonalna projekcija okomitih pravaca

Već smo prije istaknuli da se veličina kuta između pravaca NE čuva pri ortogonalnom projiciranju, pa stoga vrijedi:

  • Ortogonalne projekcije dva okomita pravca, koji su u općem položaju prema ravnini projekcije, NISU okomiti pravci.

Kao i svaki drugi kut, i pravi će se kut ortogonalno projicirati u pravoj veličini ako su mu krakovi paralelni s ravninom projekcije.

Međutim, za razliku od ostalih kutova, za pravi kut vrijedi i sljedeće:

  • Pravi se kut projicira ortogonalno u pravoj veličini ako mu je jedan krak paralelan s ravninom projekcije.

Dokaz ove tvrdnje lako se prati uz sliku 167.

Slika 167

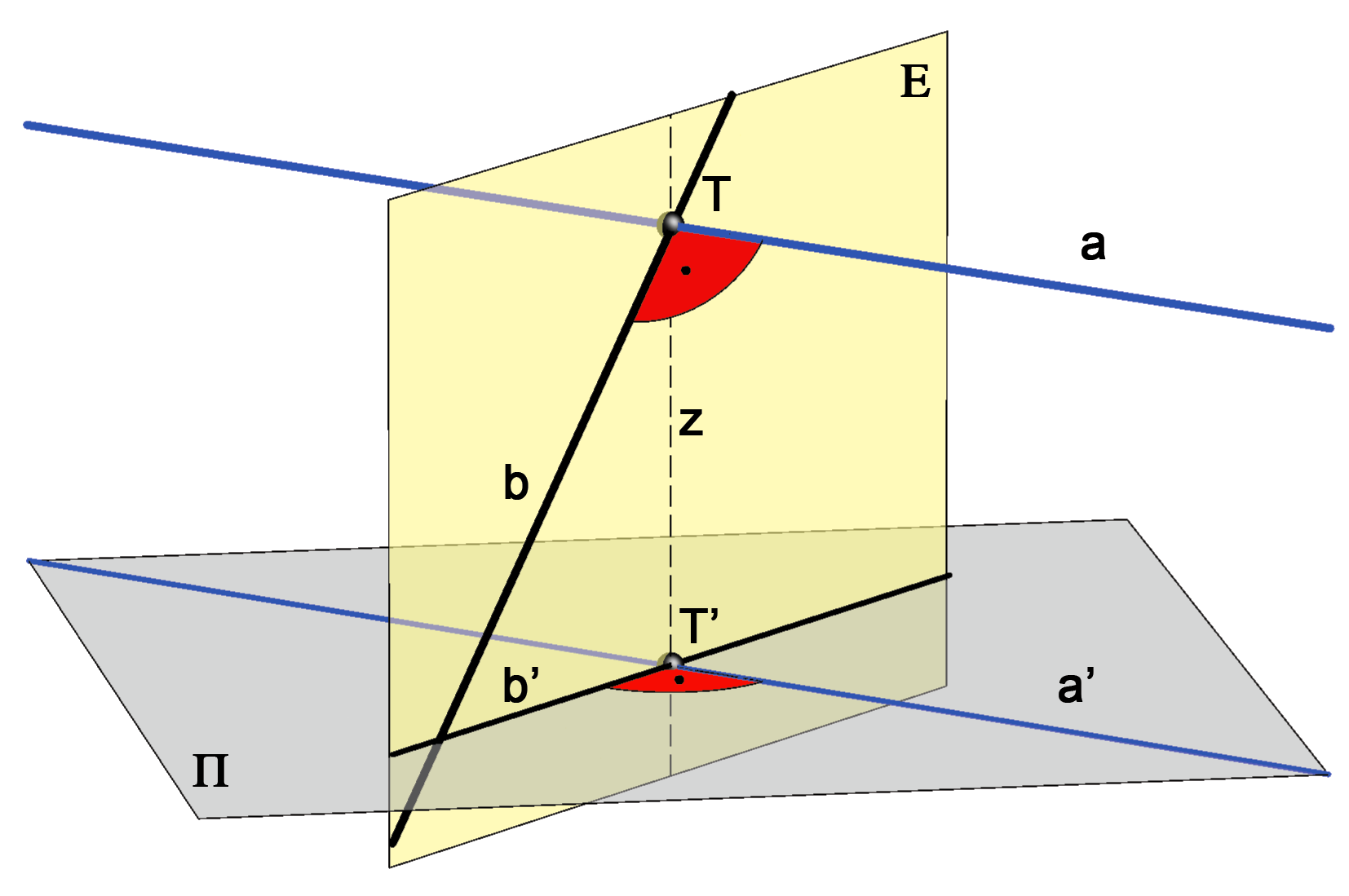
Pravac \(\small a\) je paralelan s ravninom projekcije \(\small\Pi\) i okomit na pravac \(\small b\). Treba dokazati da su tada ortogonalne projekcije tih pravaca također okomite, odnosno da je \(\small a'\perp b'\).

  • Pravac \(\small a\) okomit je na projicirajuću ravninu \(\small\mathrm E\) koja prolazi pravcem \(\small b\). Naime, \(\small a\) je okomit na dva pravca te ravnine: na pravac \(\small b\) i na zraku projiciranja \(\small z\) (okomit je na \(\small z\) jer je paralelan s ravninom \(\small\Pi\), a projiciranje je ortogonalno).
  • Kako je pravac \(\small a'\) paralelan s pravcem \(\small a\), slijedi da je i okomit na ravninu \(\small\mathrm E\). Dakle, \(\small a'\) je okomit na sve pravce ravnine \(\small\mathrm E\), pa i na pravac \(\small b'\).

Ovaj dokaz možemo kraće zapisati na sljedeći način:
\(\small a\perp b\,\,\land\,\, a\parallel\Pi\,\,\,\Longrightarrow\,\,\,a\perp\mathrm E \,\,\,\Longrightarrow\,\,\, a'\perp\mathrm E\,\,\,\Longrightarrow\,\,\, a'\perp b'\).

Okomitost pravca i ravnine

Pravac \(\small n\) koji je okomit na ravninu \(\small \mathrm P\) nazivamo okomicom ili normalom ravnine \(\small \mathrm P\), a probodište \(\small N=n\cap\mathrm P\) nazivamo nožištem normale \(\small n\).

  • Pravac \(\small n\) je okomit na ravninu \(\small \mathrm P\) ako i samo ako su njegove projekcije okomite na odgovarajuće tragove, odnosno

    \( n\perp\mathrm P\,\,\Longleftrightarrow \,\,n'\perp r_1\,\,\land\,\,n''\perp r_2.\)

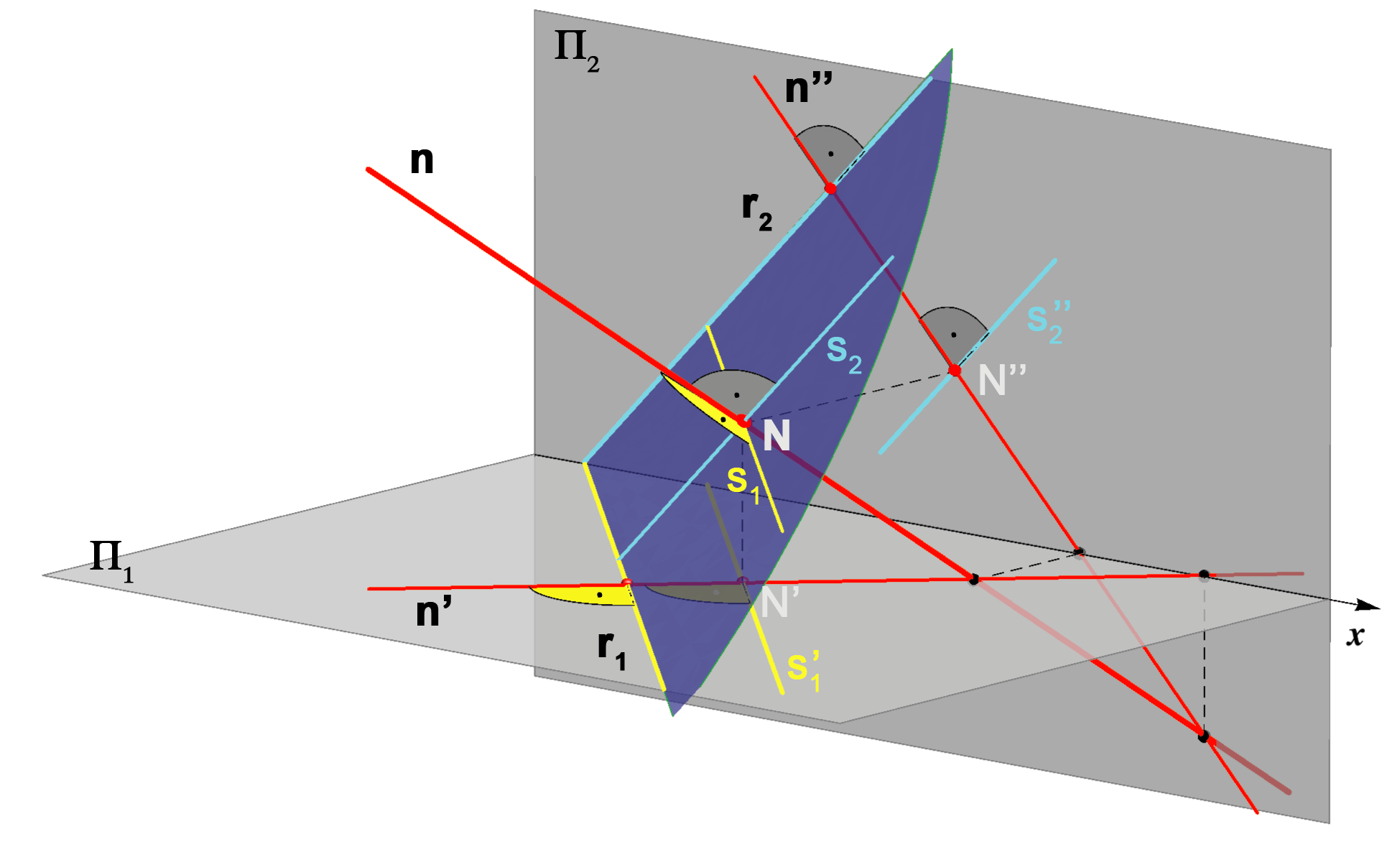
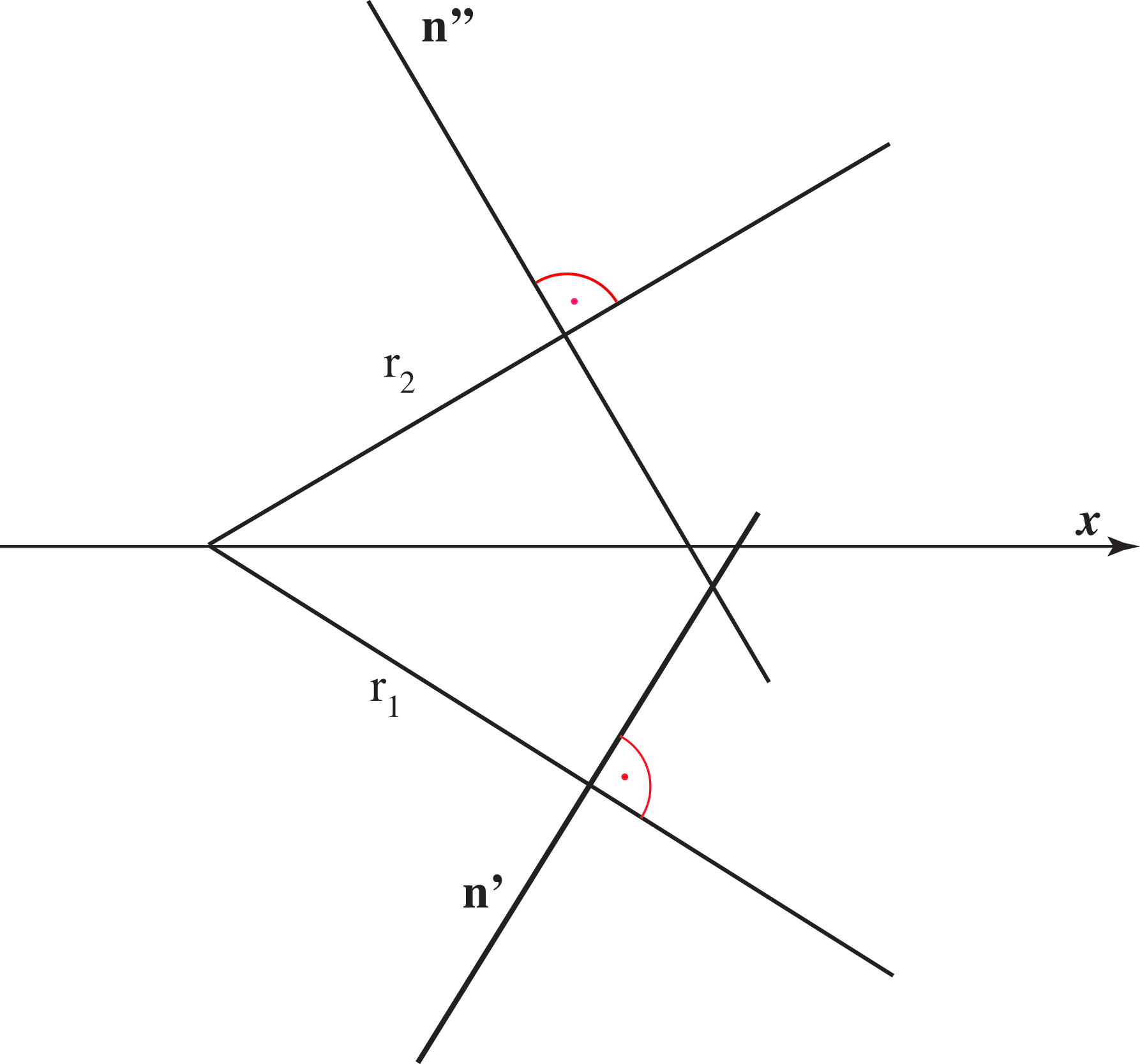
Gornja tvrdnja slijedi iz činjenice da je pravac koji je okomit na ravninu, okomit na sve pravce te ravnine, pa i na njezine tragove. Budući da je pravac okomit na trag \(\small r_1 (r_2)\) koji leži u ravnini \(\small \Pi_1(\Pi_2)\) taj će se pravi kut u tlocrtu (nacrtu) projicirati u pravoj veličini. Na slikama 168 i 169, koje vizualiziraju to svojstvo, istaknute su i one sutražnice ravnine koje sijeku normalu \(\small n\), odnosno koje prolaze nožištem normale.

Slika 168
Slika 169

Zadatak 1: Konstruirajte projekcije pravca koji prolazi zadanom točkom, a okomit je na ravninu zadanu tragovima.

Zadatak 2: Konstruirajte tragove ravnine koja prolazi zadanom točkom, a okomita je na zadani pravac.RJEŠENJE (Prezentacija 17)

Zadatak 3: Odredite udaljenost zadane točke od ravnine zadane tragovima. RJEŠENJE(Prezentacija 18)

Zadatak 4: Odredite udaljenost zadane točke od zadanog pravca. RJEŠENJE (Prezentacija 19)

Simetralna ravnina dužine

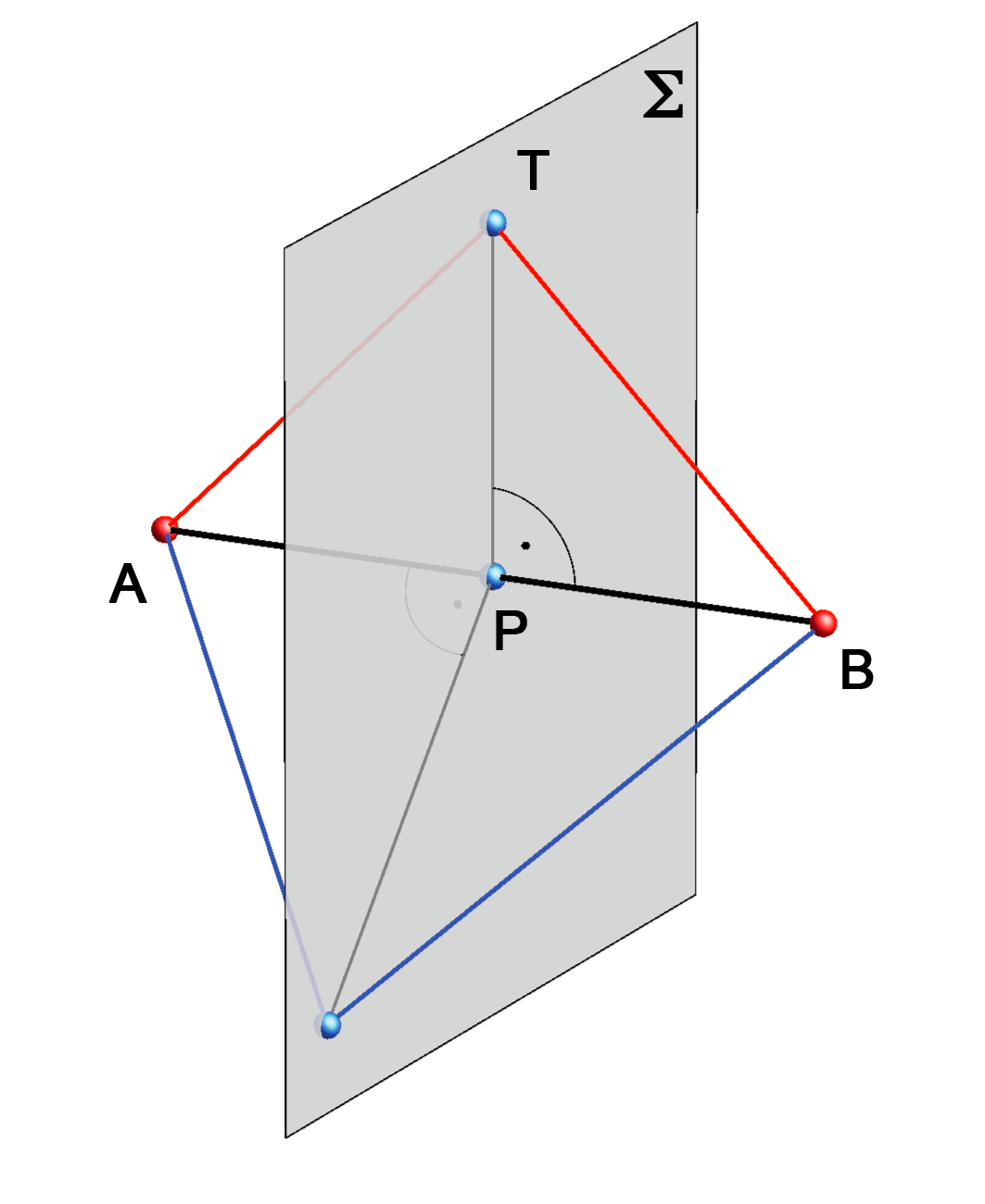
Slika 170: \(\small T \in\Sigma\,\,\Longleftrightarrow \,\,d(A,T) = d(B,T)\)
  • Skup svih točaka prostora koje su jednako udaljene od krajnjih točaka neke dužine \(\small \overline{AB}\) leži u jednoj ravnini koju nazivamo simetralnom ravninom dužine \(\small \overline{AB}\).
  • Simetralna ravnina dužine \(\small \overline{AB}\) prolazi njezinim polovištem i okomita je na pravac \(\small AB\).

Zadatak 5: Konstruirajte tragove simetralne ravnine dužine \(\small\overline {AB}[A(0,1,5),B(3,4,4)]\).

Prevaljivanje normale

Neka je pravac \(\small n\) okomit na ravninu \(\small \mathrm P\) i neka je točka \(\small N\) njihovo probodište. Neka je, nadalje, pravac \(\small p_1\) priklonica 1. skupine ravnine \(\small \mathrm P\) kroz točku \(\small N\), a pravac \(\small p_2\) priklonica 2. skupine iste ravnine koja također prolazi točkom \(\small N\).

Zbog svojstva projiciranja okomice na ravninu (\(\small n'\perp r_1\), \(\small n''\perp r_2\)), jasno je da će se tlocrt pravca \(\small n\) podudarati s tlocrtom priklonice \(\small p_1\) (\(\small n' = p'_1\)), a nacrt pravca \(\small n\) s nacrtom priklonice \(\small p_2\) (\(\small n'' = p''_2\)). To znači da pravci \(\small n\) i \(\small p_1\) leže u istoj 1. projicirajućoj ravnini, dok \(\small n\) i \(\small p_2\) leže u istoj 2. projicirajućoj ravnini. Ta su svojstva prikazana na slikama 171-174.

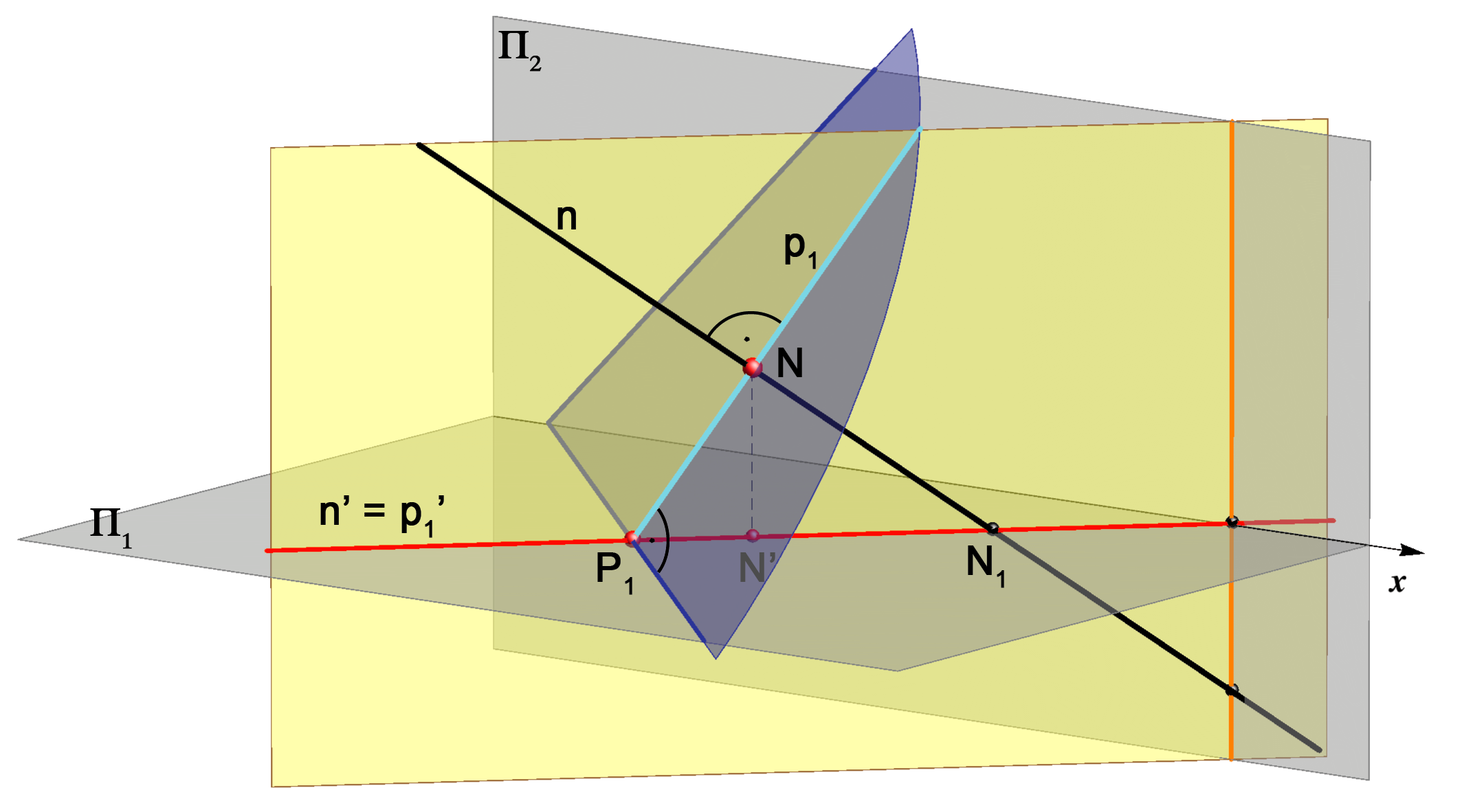
Slika 171: Normala ravnine i priklonica 1. skupine kroz
njezino nožište leže u istoj 1. projicirajućoj ravnini
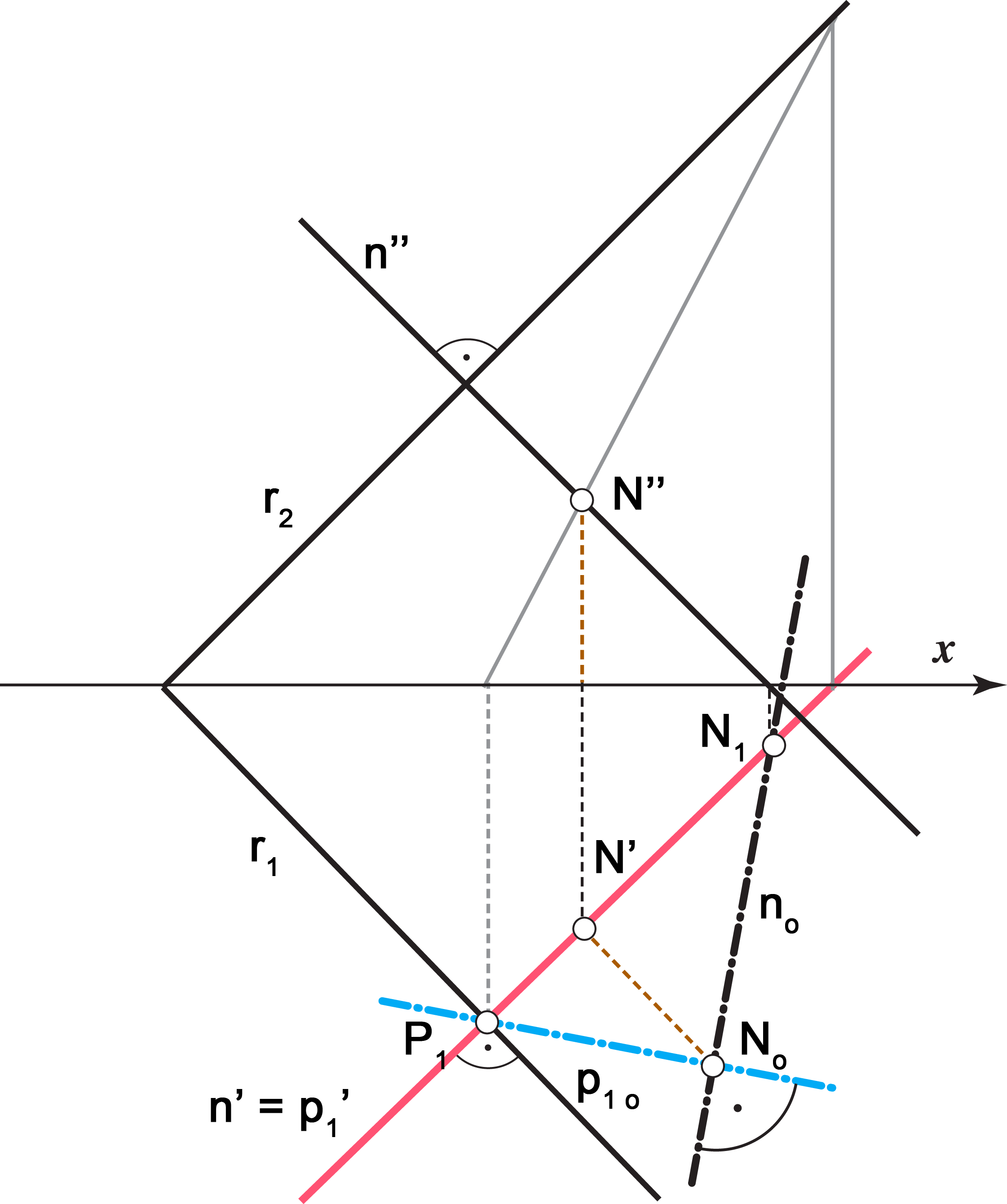
Slika 172: Normala prevaljena u \(\small \Pi_1\) okomita je na
prevaljenu priklonicu 1. skupine, a siječe ju u prevaljenom nožištu
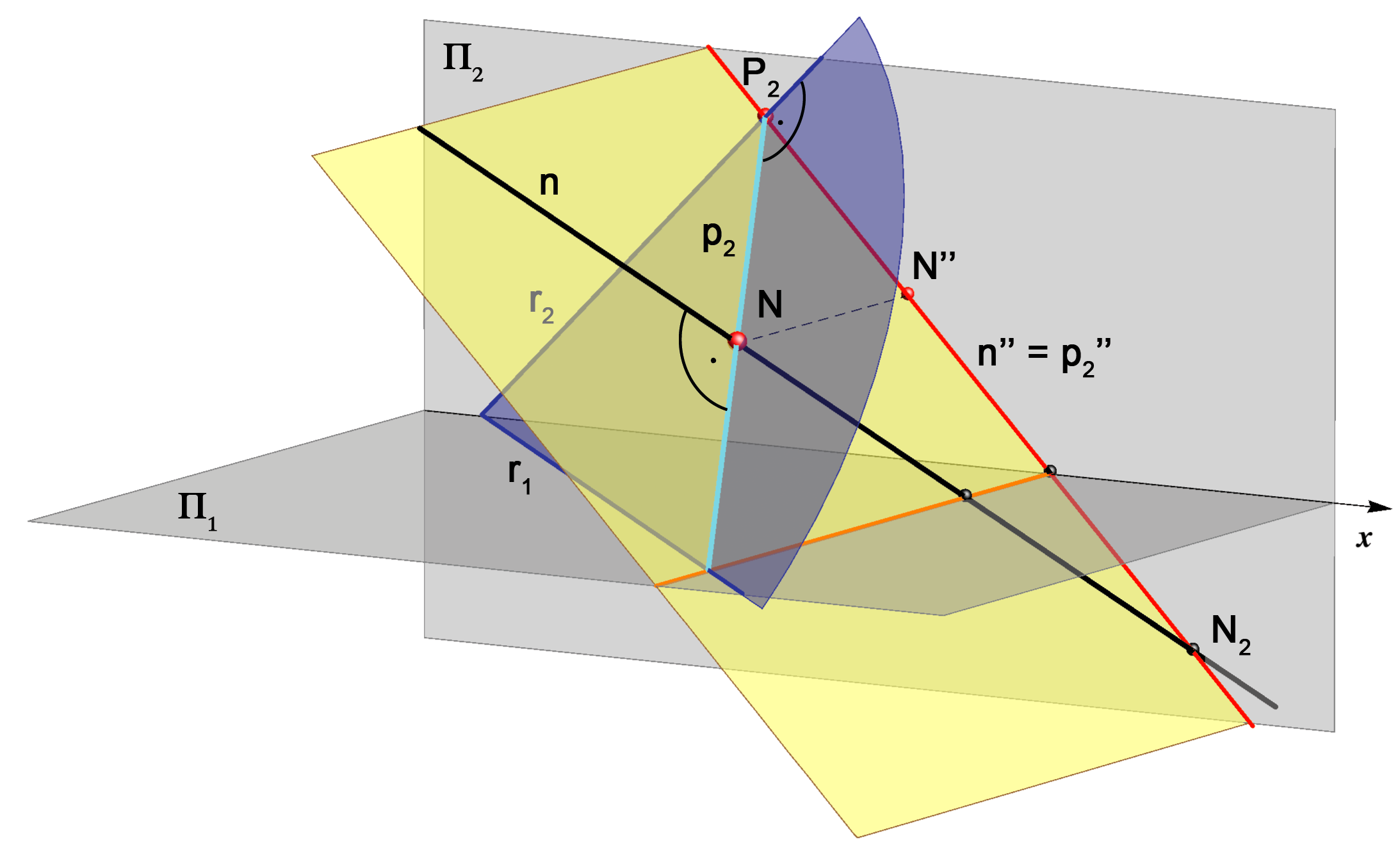
Slika 173: Normala ravnine i priklonica 2. skupine kroz
njezino nožište leže u istoj 2. projicirajućoj ravnini
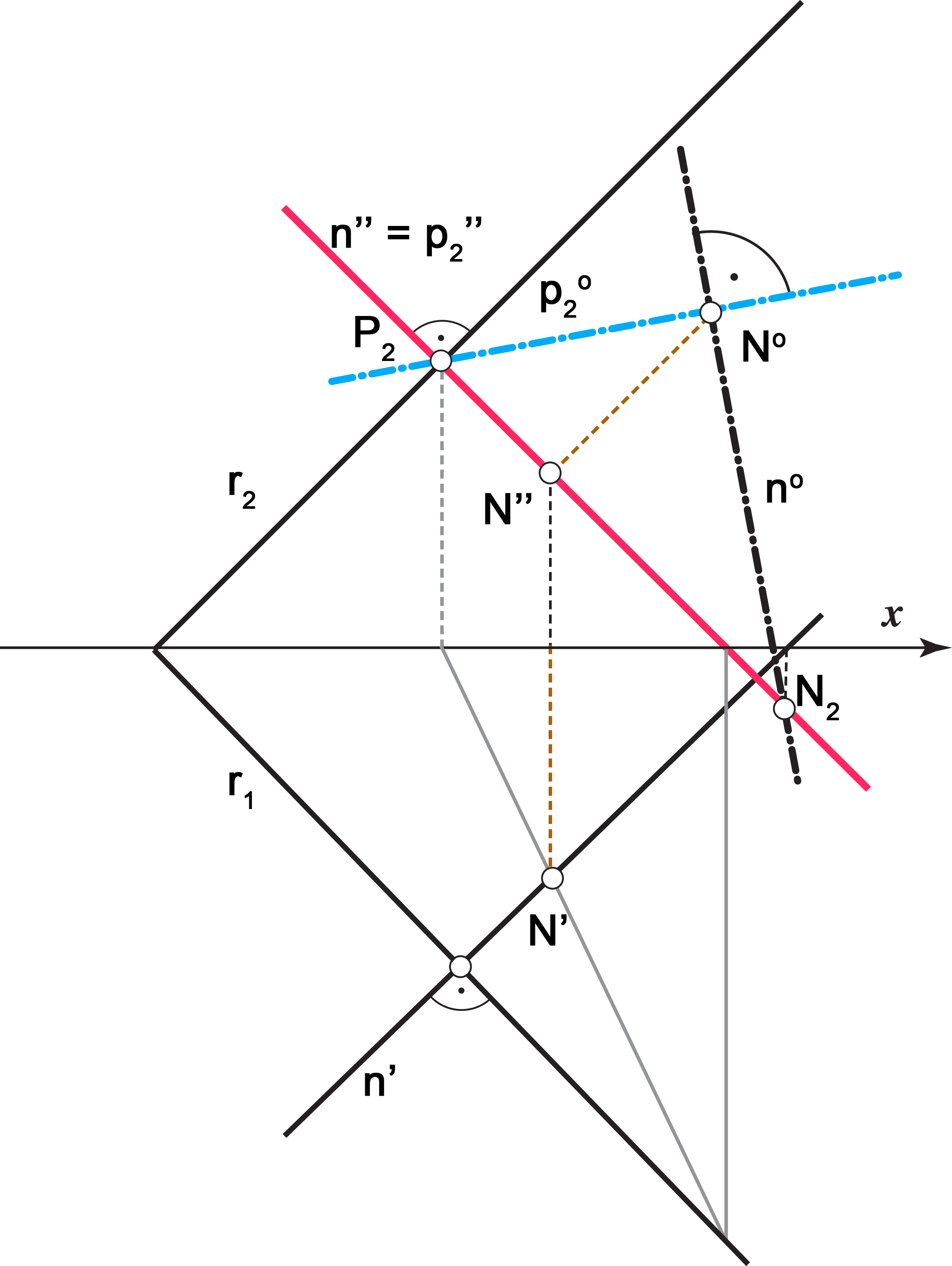
Slika 174: Normala prevaljena u \(\small \Pi_2\) okomita je na
prevaljenu priklonicu 2. skupine, a siječe ju u prevaljenom nožištu

Zadatak 6: Iz točke \(\small T(1,3,-)\) ravnine \(\small \mathrm P(3,3,-5)\) uzdignite okomicu na tu ravninu duljine 4. RJEŠENJE (Prezentacija 20)

Okomitost dviju ravnina

Dvije su ravnine okomite ako jedna od tih ravnina sadrži barem jedan pravac koji je okomit na drugu ravninu.

Tada svaka od njih sadrži beskonačno mnogo pravaca (pramen paralelnih pravaca) koji su okomiti na drugu ravninu.

U Mongeovom projiciranju okomitost dviju ravnina ne može se očitati iz položaja njihovih tragova, naime, njihovi odgovarajući tragovi nisu okomiti. Provjerite tu tvrdnju na nekom primjeru koji vam je lako zamisliti.

Zadatak 7: Zadanim pravcem postavite ravninu koja je okomita na zadanu ravninu. RJEŠENJE (Prezentacija 21)