Plohu nazivamo pravčastom ako kroz svaku njezinu točku prolazi barem jedan pravac koji cijeli leži na toj plohi. Takve plohe dijelimo na razvojne i vitopere.

  • Razvojne (razmotljive ili developabilne) pravčaste plohe mogu se bez rastezanja i kidanja razviti u ravninu. Ovoj grupi ploha pripadaju svi stošci i valjci te plohe čije su izvodnice tangente neke prostorne krivulje. Sve točke razmotljive pravčaste plohe su paraboličke

  • Vitopere (nerazmotljive) pravčaste plohe ne mogu se bez savijanja i kidanja razviti u ravninu. Gotovo sve točke vitopere pravčaste plohe su hiperboličke, a mogu se pojaviti i neke paraboličke točke. Linije vitoperih pravčastih ploha koje sadrže paraboličke točke nazivamo torzalnim linijama plohe

  • Na pravčastim plohama ne postoje eliptičke točke

1. Konstrukcija vitopere pravčaste plohe

Animacija 67: Izvodnice plohe su transverzale krivulja \(\small k_1\), \(\small k_2\) i \(\small k_3\)

Postoji više načina konstruktivnog izvođenja pravčastih ploha. Jedan od njih (koji koristimo u okviru našeg kolegija) je taj da su pravčaste plohe sustavi pravaca koji sijeku tri prostorne krivulje \(\small k_1\), \(\small k_2\) i \(\small k_3\).

Prostorne krivulje \(\small k_1\), \(\small k_2\) i \(\small k_3\) nazivamo ravnalicama, a pravce koji ih sijeku izvodnicama pravčaste plohe.

2. Konoidi

Animacija 68: Izvodnice plohe su transverzale krivulja \(\small k_1\), \(\small k_2\) i \(\small k_3^\infty\)

Pravčaste plohe kojima je jedna ravnalica beskonačno daleki pravac nazivamo konoidima.

Ravnine koje sadrže takvu beskonačno daleku ravnalicu nazivamo direkcijskim ravninama pravčaste plohe.

3. Stupanj algebarske pravčaste plohe

Ako se kao ravnalice odaberu algebarske krivulje (koje su karakterizirane redom i razredom) nastaje algebarska pravčasta ploha. Red i razred takve plohe uvijek se podudaraju, odnosno algebarske pravčaste plohe imaju stupanj. Za izračunavanje stupnja pravčaste plohe koristimo sljedeće teoreme.

Teorem

Ako ravnalice \(\small k_1\), \(\small k_2\) i \(\small k_3\), redova \(\small n_1\), \(\small n_2\) i \(\small n_3\), nemaju zajedničkih točaka, tada je red pravčaste plohe jednak \(\small 2\cdot n_1\cdot n_2\cdot n_3\).

Međutim, ako se primjerice ravnalice \(\small k_1\) i \(\small k_2\) sijeku u jednoj točki, tada svi pravci koji prolaze tom točkom, a sijeku krivulju \(\small k_3\), pripadaju plohi i formiraju stožac reda \(\small n_3\). Pravčasta se ploha raspada na stožac reda \(\small n_3\) i ostatak koji je reda \(\small 2\cdot n_1\cdot n_2\cdot n_3-n_3\). Upravo je taj ostatak ono što smatramo izvedenom pravčastom plohom i što konstruktivno obrađujemo.

Za opći slučaj vrijedi sljedeći teorem.

Teorem

Ako se krivulje \(\small k_1\) i \(\small k_2\) sijeku u \(\small s_3\), krivulje \(\small k_1\) i \(\small k_3\) u \(\small s_2\), a krivulje \(\small k_2\) i \(\small k_3\) u \(\small s_1\) točaka, tada je red pravčaste plohe jednak \(\small 2\cdot n_1\cdot n_2\cdot n_3-(n_1\cdot s_1+n_2\cdot s_2+n_3\cdot s_3)\).

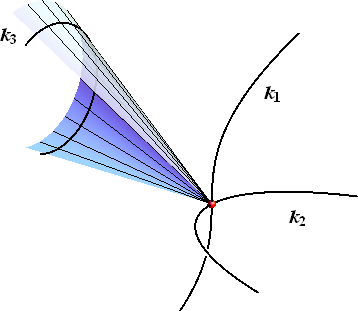
Slika 419: \(\small s_3=1\), \(\small n_3=2\) \(-\) od plohe se izuzimaju izvodnice stošca
2. stupnja pa se njezin red umanjuje za 2
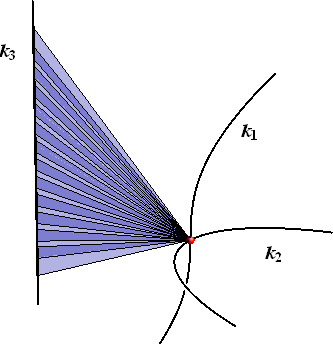
Slika 420: \(\small s_3=1\), \(\small n_3=1\) \(-\) od plohe se izuzima pramen pravaca u ravnini
pa se red plohe umanjuje za 1

4. Višestruke linije pravčastih ploha

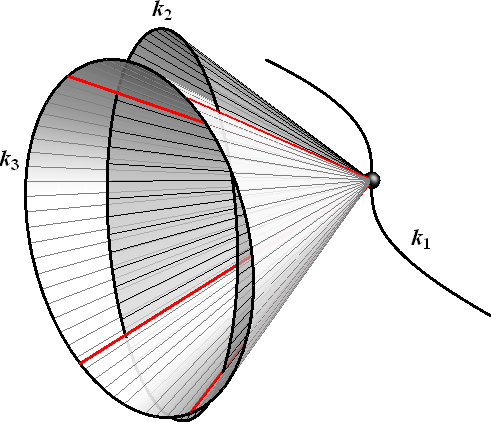
Slika 421: U slučaju \(\small n_2=n_3=2\), krivulja \(\small k_1\) je četverostruka linija plohe.
Svakom točkom te krivulje prolaze četiri izvodnice plohe

Višestrukom (dvostrukom, trostrukom, \(\small n-\)strukom) linijom pravčaste plohe nazivamo onu krivulju na plohi za koju vrijedi da svakom njezinom točkom prolazi više (2, 3, \(\small n\)) izvodnica plohe.

Izvodnice plohe koje prolaze primjerice nekom točkom ravnalice \(\small k_1\) zajedničke su izvodnice dvaju stožaca određenih vrhom u toj točki te ravnalicama \(\small k_2\) i \(\small k_3\). Takva dva stošca sa zajedničkim vrhom sijeku se u raspadnutoj krivulji reda \(\small n_2\cdot n_3\), odnosno u \(\small n_2\cdot n_3\) pravaca. Vidi sliku 421.

Ako se ravnalice sijeku, neke od izvodnica pripadat će onom dijelu raspada plohe koji izuzimamo pa za opći slučaj vrijedi sljedeći teorem.

Teorem

Višestruke linije algebarske pravčaste plohe su njezine ravnalice \(\small k_1\), \(\small k_2\) i \(\small k_3\) sa stupnjevima višestrukosti redom \(\small n_2\cdot n_3-s_1\), \(\small n_1\cdot n_3-s_2\) i \(\small n_1\cdot n_2-s_3\).

5. Dirne ravnine pravčastih ploha

Za dirne ravnine pravčastih ploha vrijedi sljedeći teorem.

Teorem

Dirna ravnina, s diralištem na izvodnici \(\small g\) algebarske pravčaste plohe stupnja \(\small n\), siječe tu plohu po izvodnici \(\small g\) i krivulji reda \(\small n-1\).

Animacija 69

U animaciji 69 prikazuje se jedan konoid 4. stupnja i promjena njegovih dirnih ravnina, ako se njihova dirališta pomiču duž jedne izvodnice konoida.

Kako je konoid ploha 4. stupnja, svaka ga dirna ravnina siječe po izvodnici i krivulji 3. reda.

U slučaju kad diralište padne na dvostruku liniju konoida, ta krivulja 3. reda raspada se na dva pravca od kojih je jedan dvostruki pravac plohe.

6. Sustavi izvodnica pravčastih ploha

Za sve pravčaste plohe stupnja većeg od 2 vrijedi da imaju samo jedan sustav izvodnica, odnosno svakom točkom takve plohe (koja ne leži na višestrukoj liniji) prolazi samo jedna izvodnica.

Samo na vitoperim pravčastim plohama 2. stupnja (jednokrilnom hiperboloidu i hiperboličkom paraboloidu) postoje dva sustava izvodnica.