Basic Types of Projection
Lines and planes which are basic elements of space, as well as all other spatial objects, are observed as sets of points.Hence, it is sufficient to define the projection of a point.
There are two basic types of projection - central and parallel.
Central projection
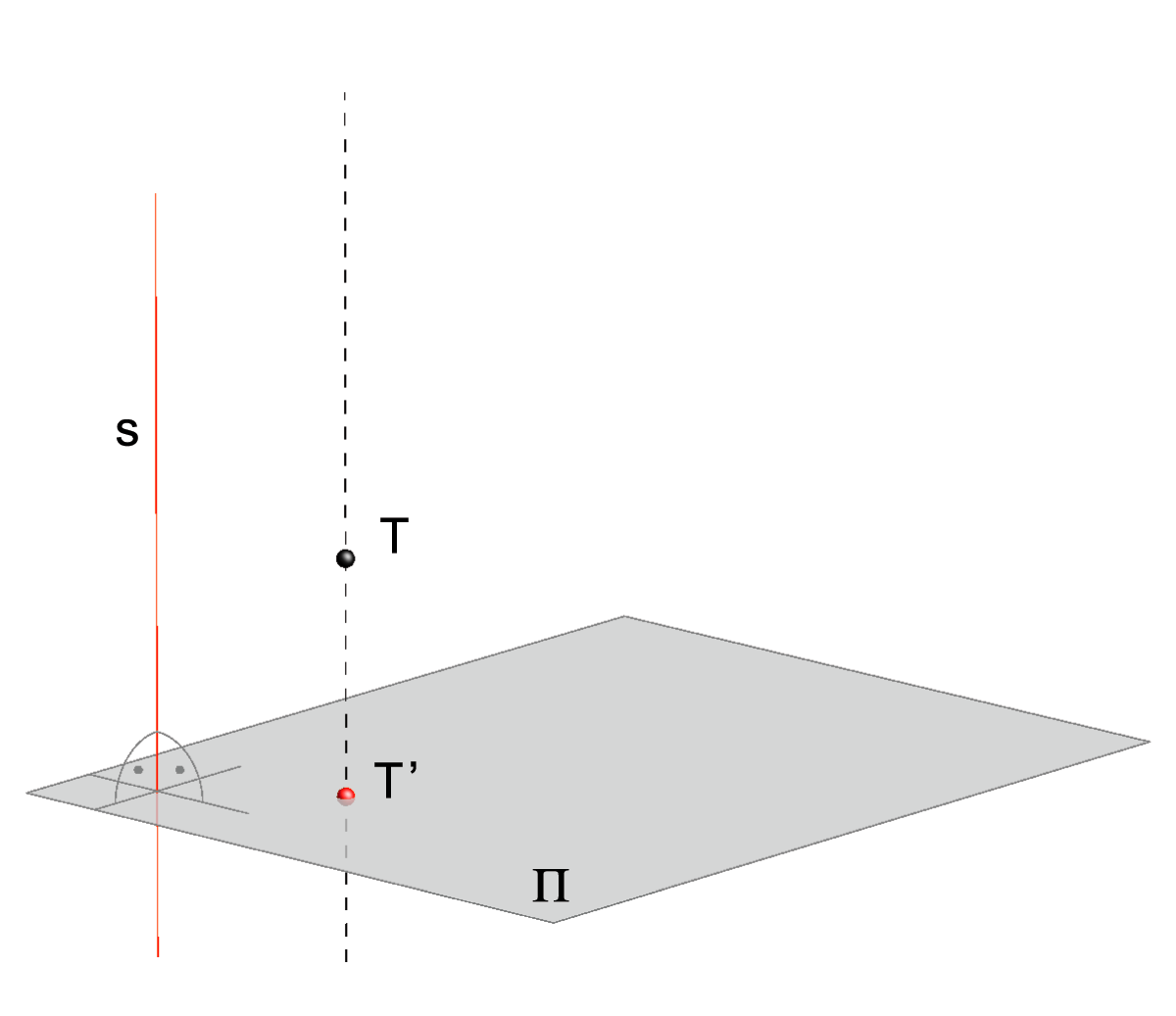
Let a plane Π and a point S be given in space such that the point S is not at infinity and not lying in the plane Π (S ∉ Π).central projection to the plane Π from S.
The point S is called the center, and the lines ST are called rays of the central projection.
The plane Π is called the projection plane or picture plane.
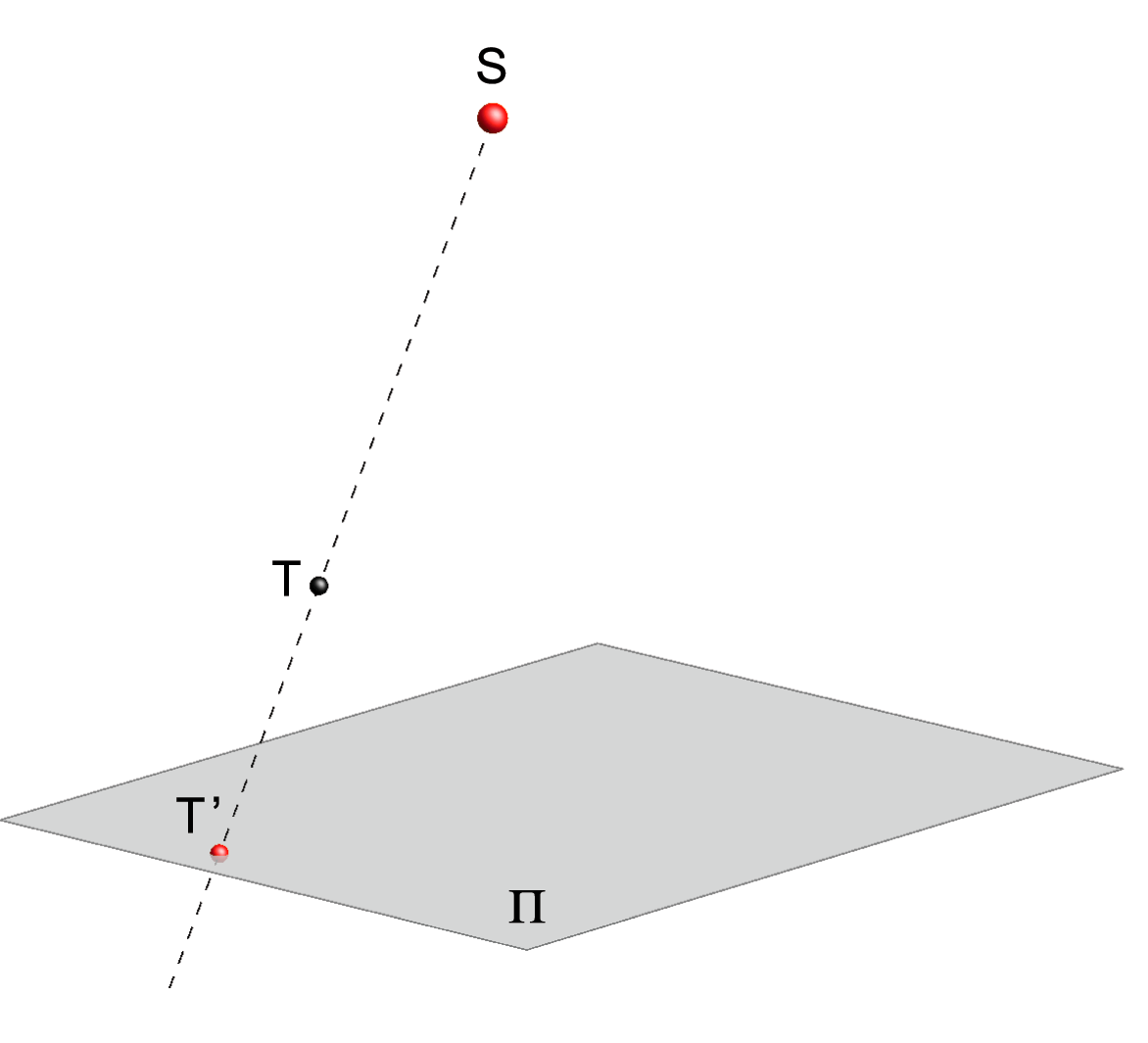 Central projection of a point T. |
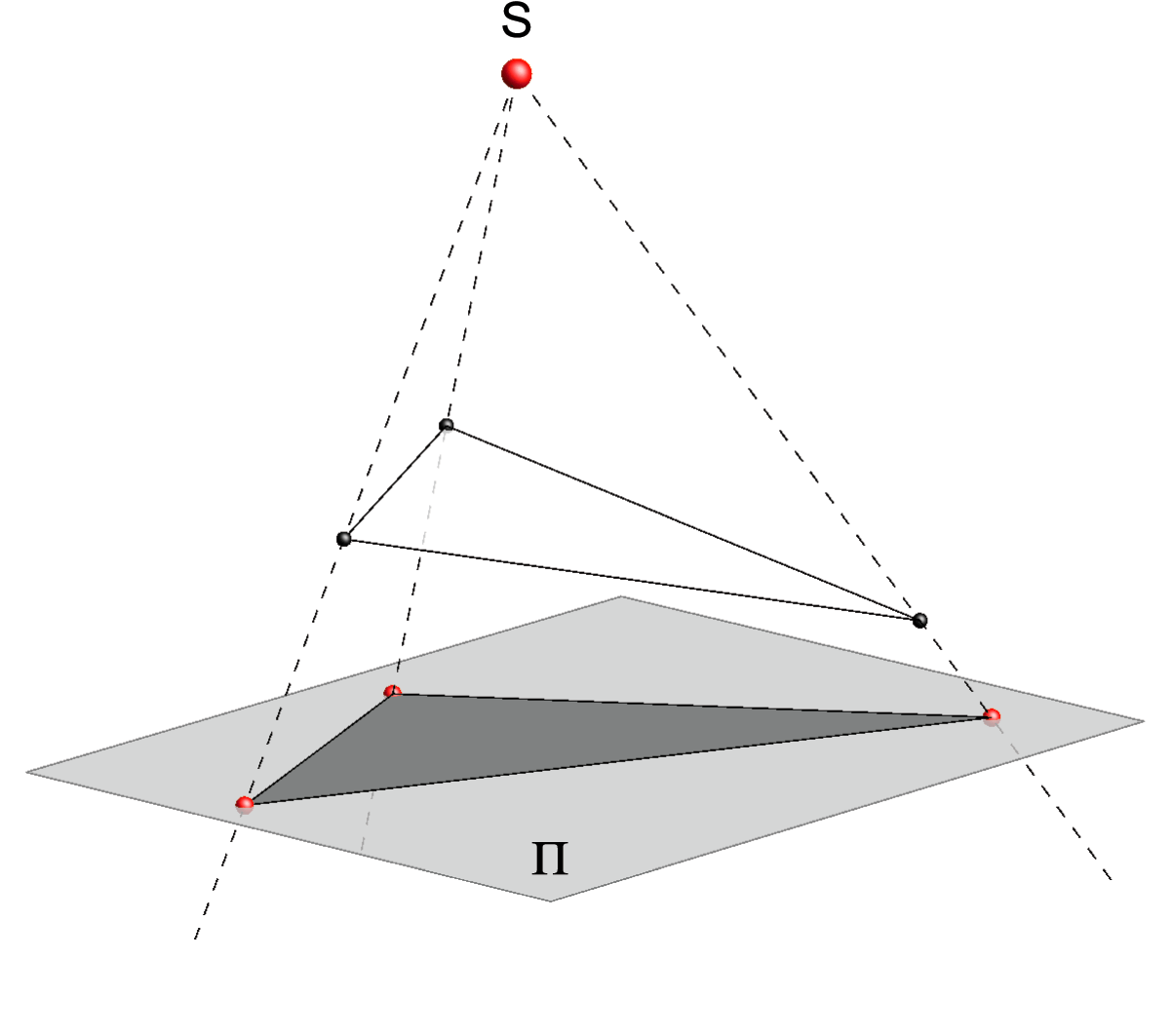
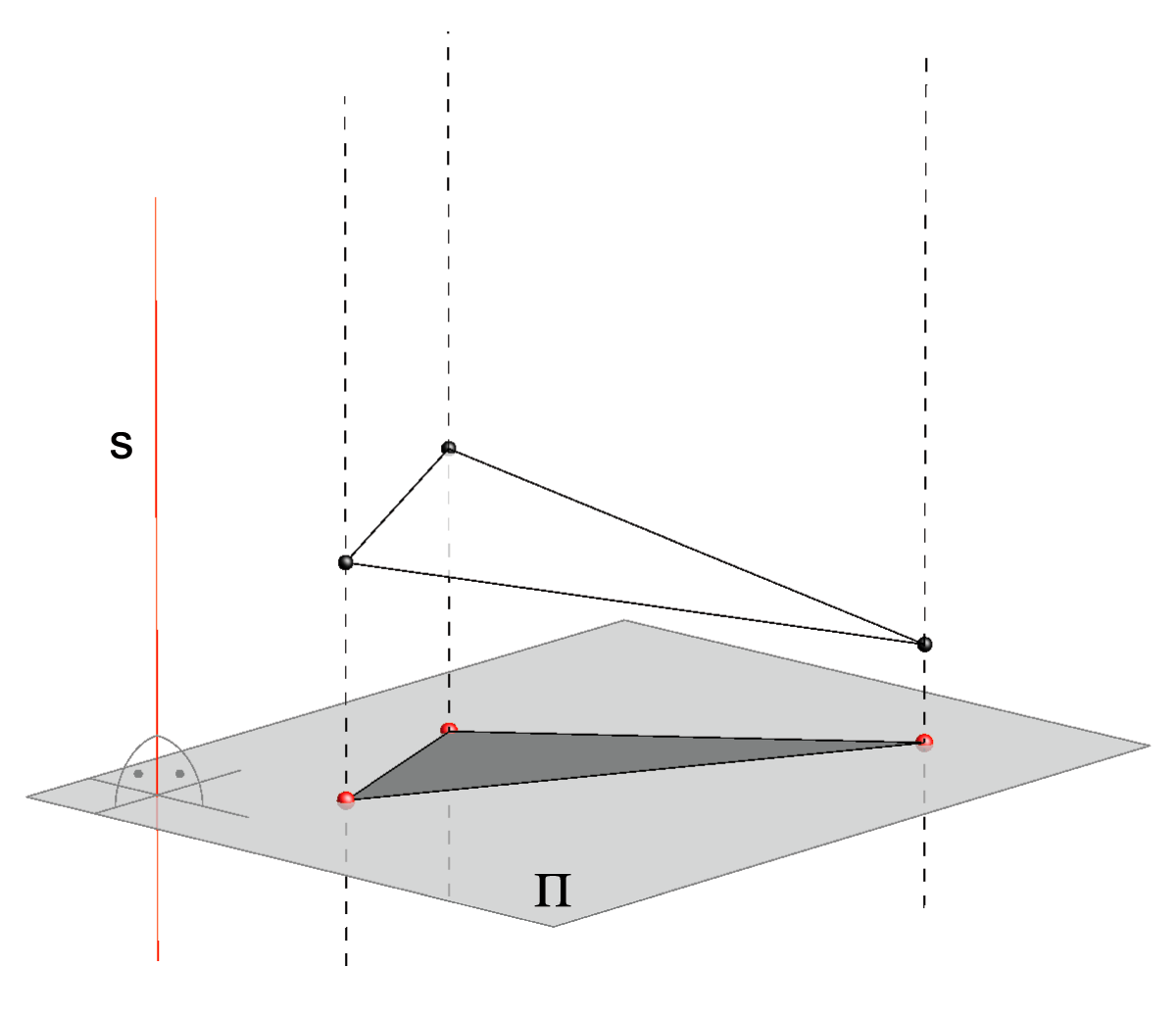
Central projection of a triangle. |
Parallel projection
Let a plane Π and a line s be given in a space such that the line s is not parallel with the plane Π.1Lines parallel with the line s are called rays of the parallel projection, and the plane Π is called the projection plane or picture plane.
All other cases of parallel projection are called oblique parallel projections.
1 A line lying in a plane is also considered to be parallel with that plane.
2 In the extended Euclidean plane a parallel projection can be interpreted as a central projection with the center at infinity.
From the fact that S∞ ∉ Π it can be deduced that the point S∞ is the point at infinity of some line that is not parallel with the plane Π.
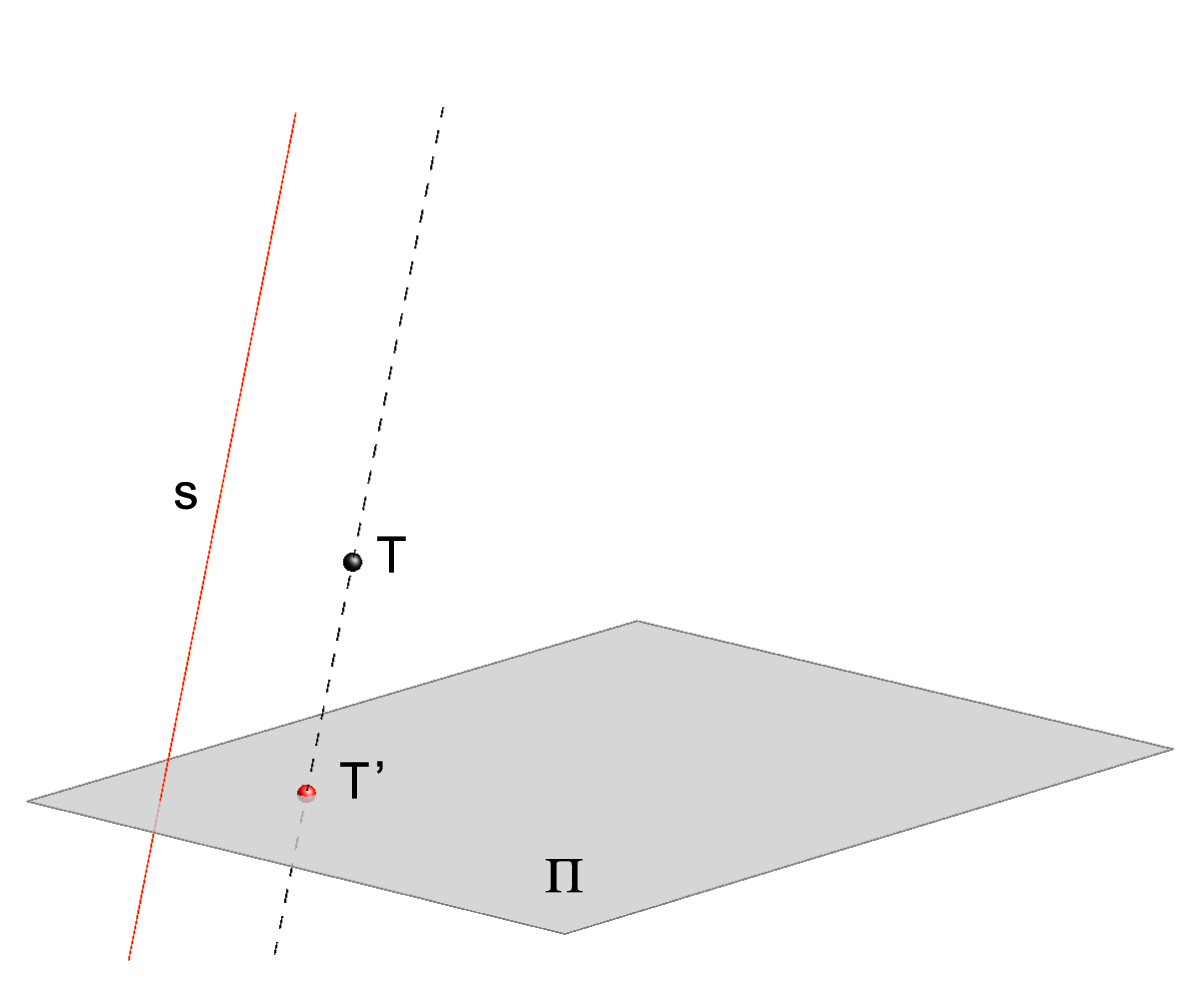
Oblique parallel projection of a point T. |
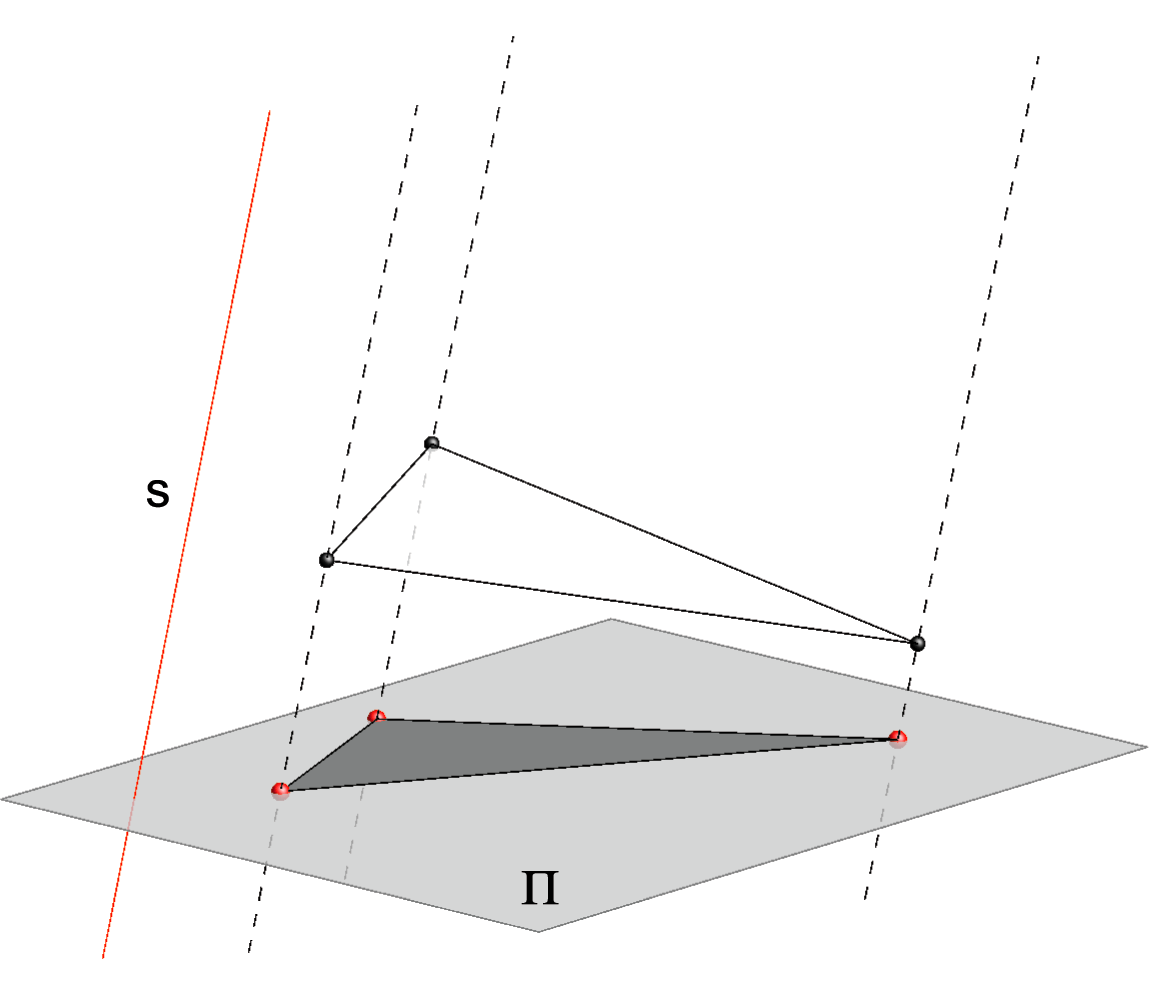
Oblique parallel projection of a triangle. |
Orthogonal projection of a point T. |
Orthogonal projection of a triangle. |
Monge's method (two picture protocol)
The loss of one dimension, in the projection of a spatial object to a plane, creates various problems when reconstructing the 3D-model from its projection.For example, all triangles whose vertices lie on the same rays of a central or parallel projection will have the same projection.
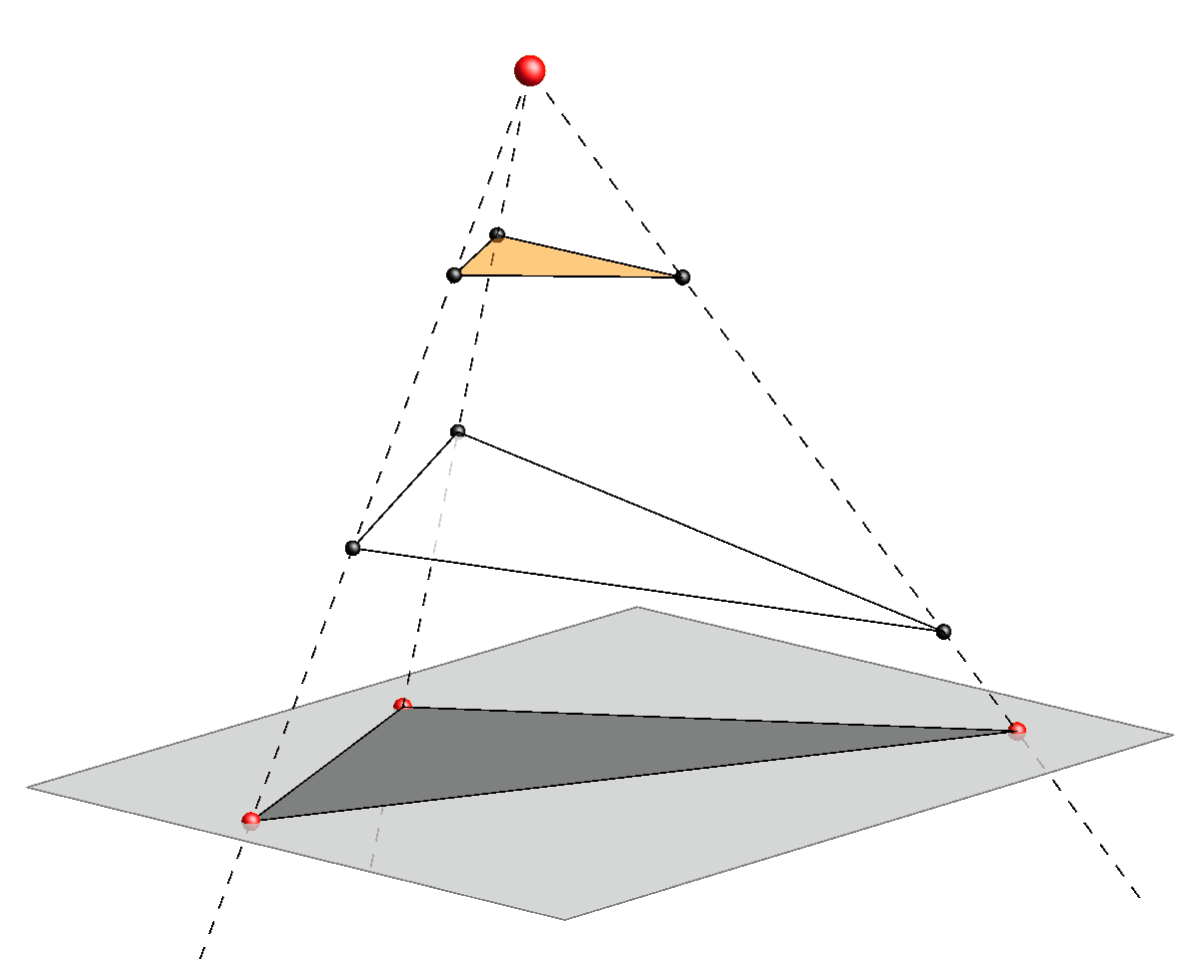
Central projection |
Oblique parallel projection |
Orthogonal projection |
If you have only one projection of a triangle in a plane Π what can you conclude about the projected object from its image?
- It can be a projection of a truncated three-sided pyramid, in the case of a central projection, or a three-sided prism, in the case of a parallel projection.
- It can be a triangle.
- There are also some other more complicated possibilities.
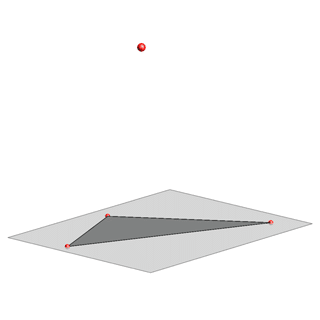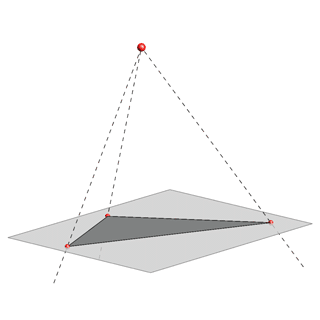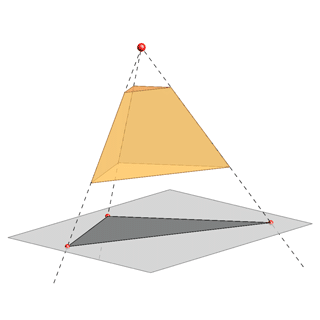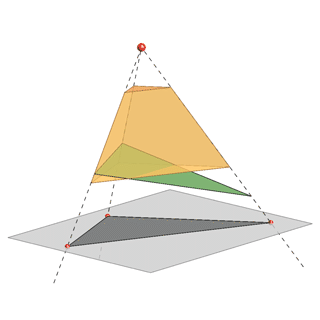
Central projection |
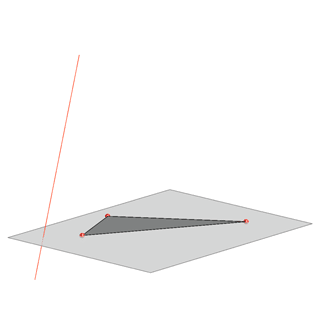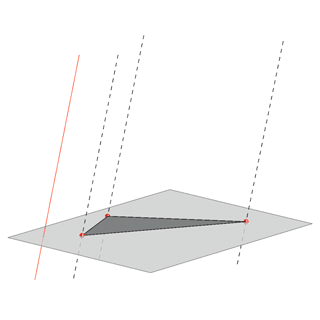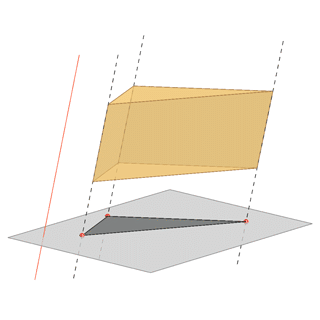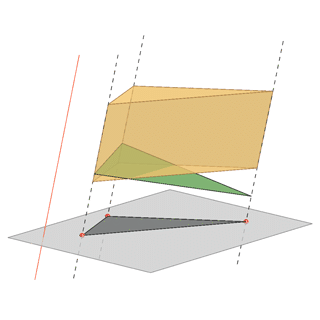
Oblique parallel projection |
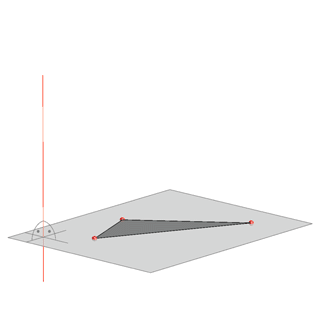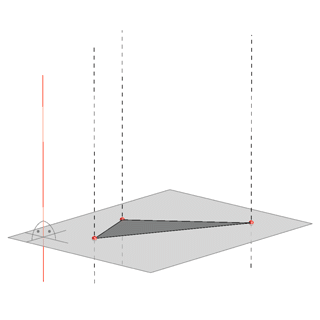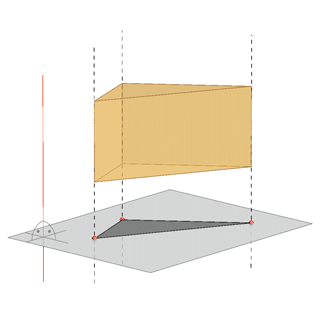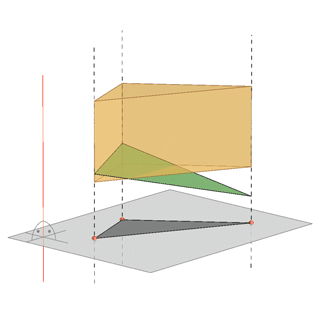
Orthogonal projection |
Such problems, when dealing with one projection, which is important for gaining an accurate image of an object, are solved in different ways: choosing a suitable object position in reference to a given projection, highlighting certain points and lines of the object etc.
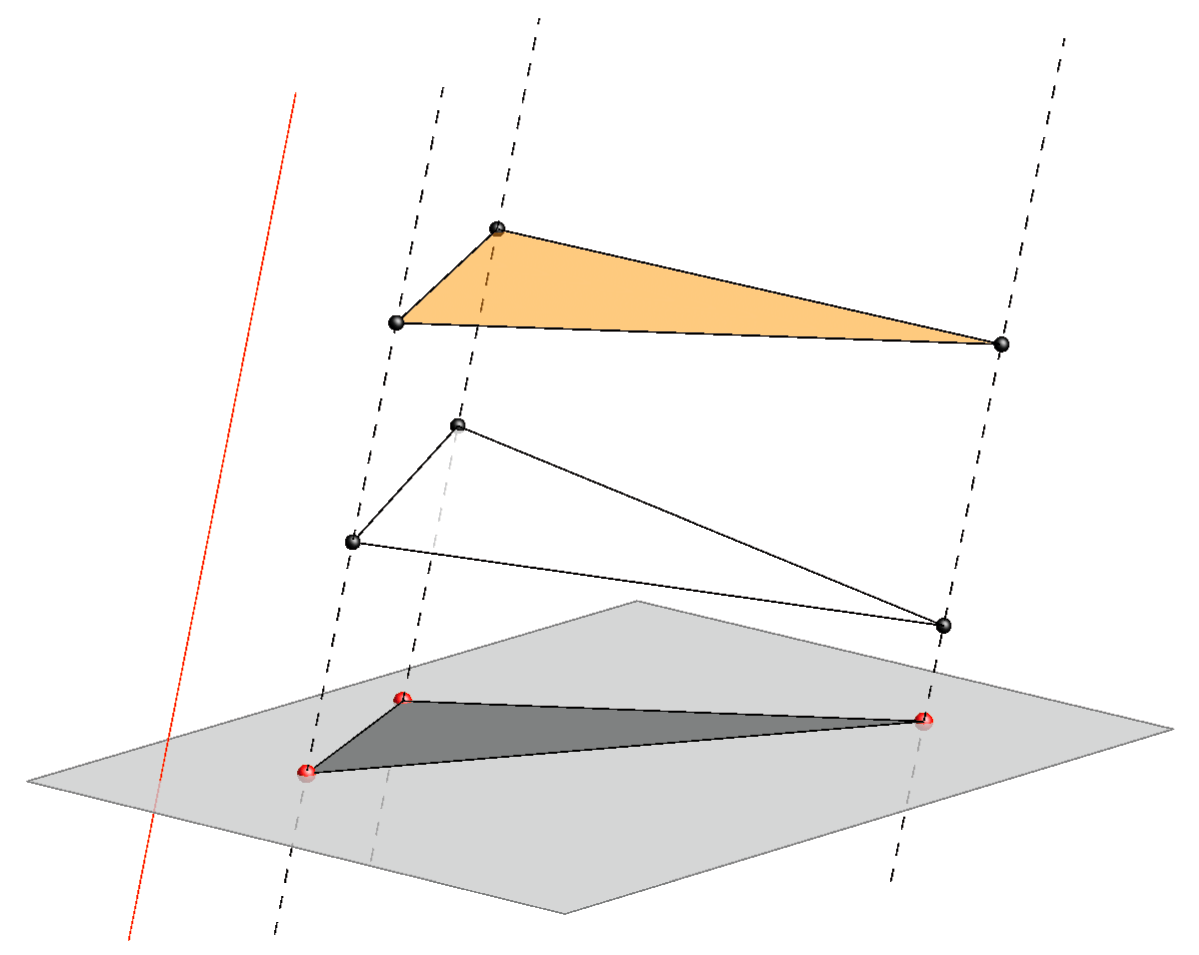
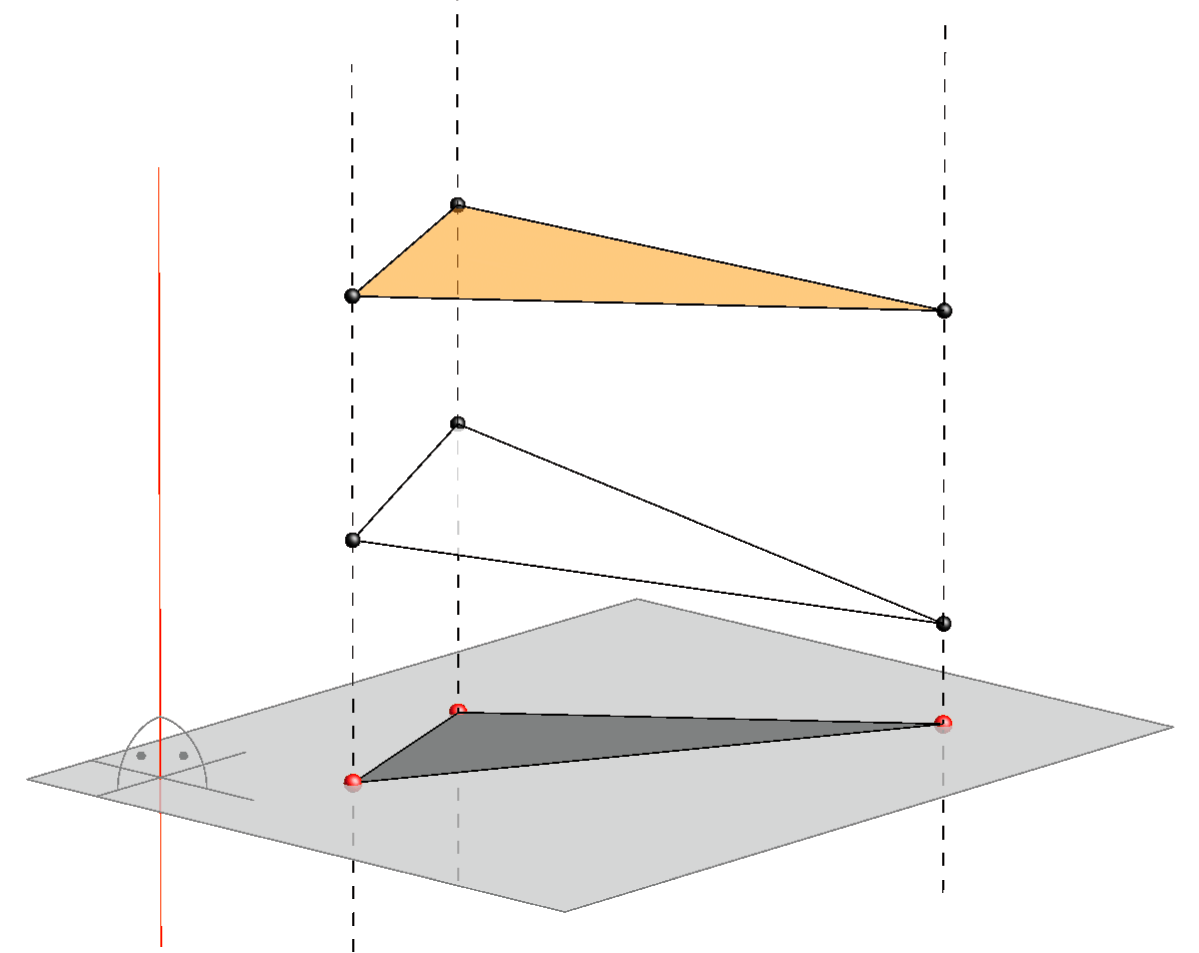
However, when the metrical and positional data of the spatial object are more important than the accuracy of its image on a drawing, as is often the case in engineering, then it is appropriate to use two orthogonal projections on two orthogonal planes.
For example, if we add another orthogonal projection in the case above of the orthogonal projection of the white and yellow triangle, as on the picture below, and simultaneously observe both projections, then the graphical data about them is considerably more useful. Now, it is clear that there are two different triangles, one (yellow) above another (white).
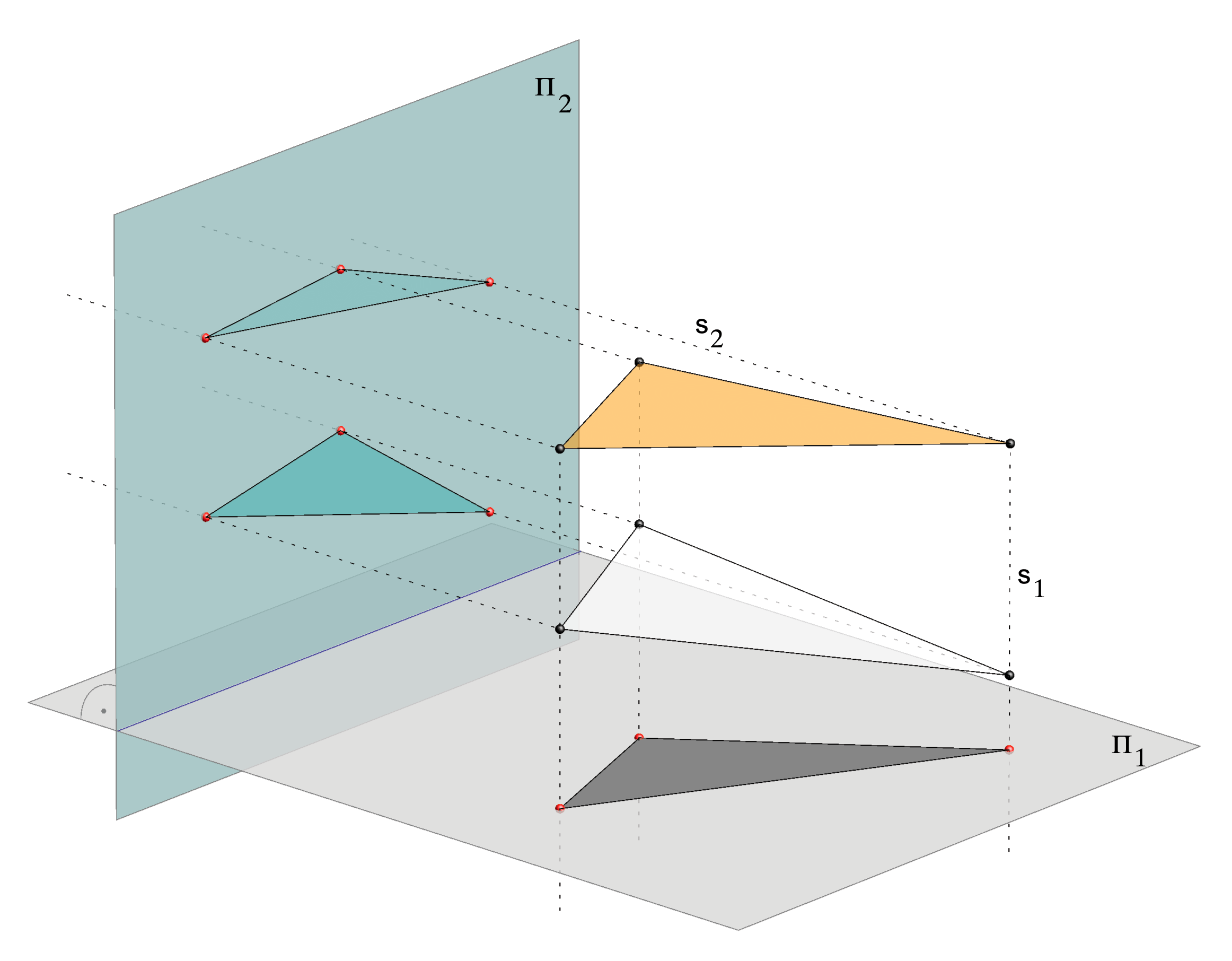
Orthogonal projections onto two orthogonal planes
Monge's method consists of:
- orthogonal projection onto two orthogonal planes where one is chosen as the drawing plane,
- rotating the orthogonal projection of the object that does not lie in the drawing plane by 90o around the intersection of the planes into the drawing plane,
- in this way we gain two connected projections of an object in the drawing plane which allows a unique and accurate reconstruction of the 3D-model.
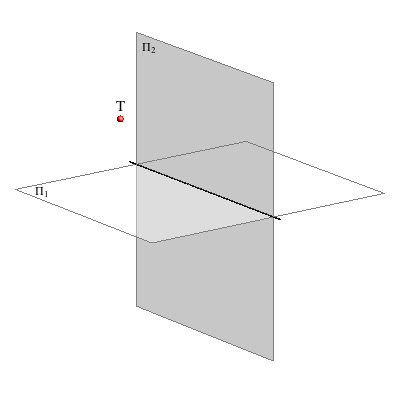
The projection planes are usually taken to be vertical and horizontal, where the vertical plane of projection is chosen as the drawing plane, and the horizontal plane of projection is rotated counterclockwise.
The pictures below represent animated illustrations of this procedure when the given object is a point T.
|
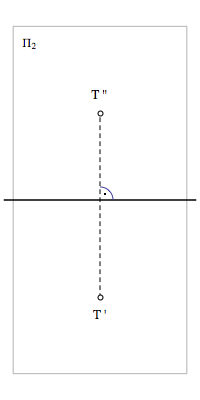 Projection of a point in the drawing plane. Projection of a point in the drawing plane.
|
|