Monge's Method of Projection

Basic elements of the Euclidean plane will be denoted in the following way:
points – capital Latin letters (A, B, C, D,...)
lines – lower-case Latin letters (a, b, c, d,...)
planes – capital Greek letters (Α, Β, Γ, Δ,...).

Projection of a Point

Let two perpendicular planes Π1 and Π2 be given in space intersecting at a line x.
The plane Π1 is horizontal and is called the 1st projection plane or horizontal projection plane or ground plane.
The plane Π2 is vertical and is called the 2nd projection plane or vertical projection plane or frontal plane.
The line of intersection x is called the ground line or reference line.

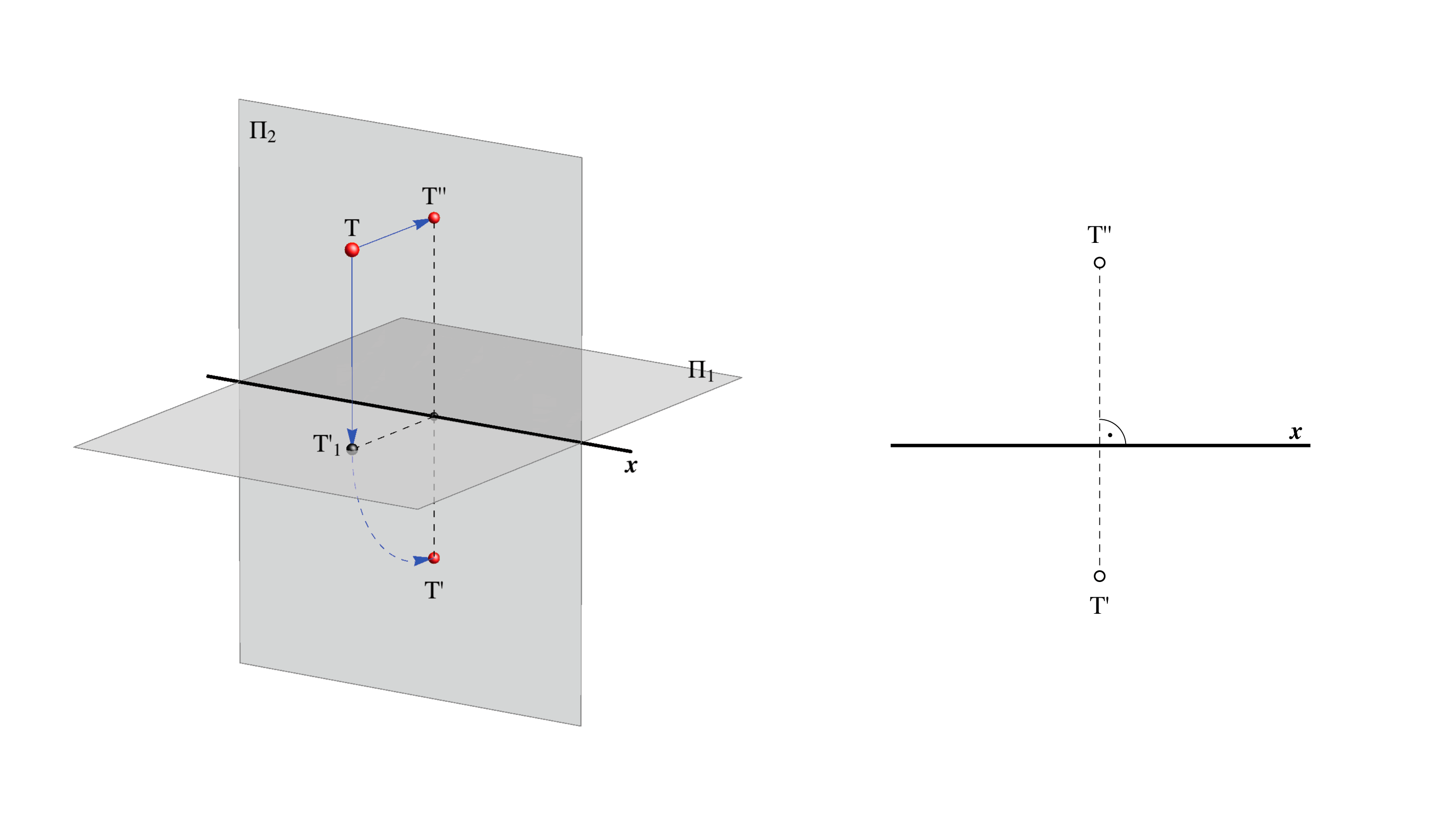
Let T be an arbitrary point in space. Orthogonal projection of the point T onto the plane Π1 is called the 1st projection or horizontal projection of the point T, and is denoted by T'1.
Orthogonal projection of the point T onto the plane Π2 is called the 2nd projection or vertical projection of the point T, and is denoted by T''.

We now rotate the plane Π1 around the intersection line x counterclockwise by 90o.
In this rotation the point T'1 transforms to the point T' on the plane Π2.
The point T' ∈ Π2 is also called the 1st projection or horizontal projection of the point T.

The correspondence T —> (T',T'') is called Monge's method of projection or the two picture protocol.

The straight line T'T'' ∈ Π2 is perpendicular to the intersection line x, and is called line of recall of the point T.

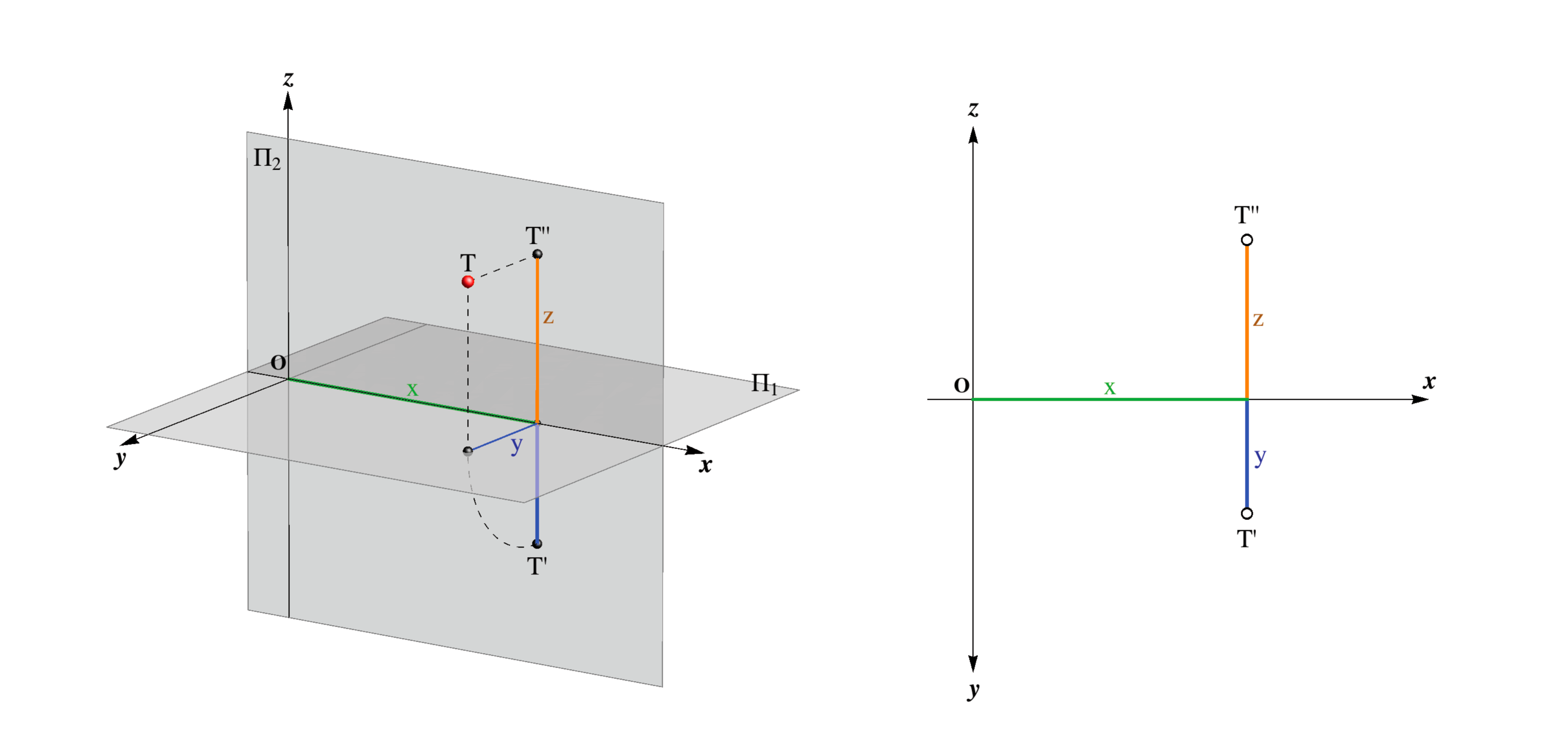
In space, we introduce a left rectangular (Cartesian) coordinate system such that the x-axis coincides with the intersection line of the planes Π1 and Π2. Now, every point T in space is determined by its coordinates T(x,y,z), for which the following applies: d(T,Π1) = |z| and d(T,Π2) = |y|.
Furthermore
  • if z = 0, then T lies in the plane Π1 (T ∈ Π1),
  • if y = 0, then T lies in the plane Π2 (T ∈ Π2).



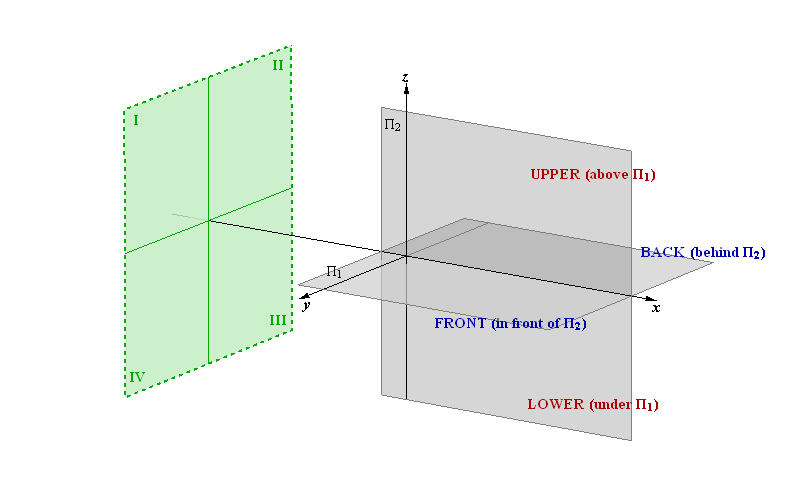
    Both projection planes Π1 and Π2 divide the space into 2 half-spaces, and together into 4 quadrants.

    Half-spaces are referred to as upper and lower (above and under the plane Π1), front and back (in front of and behind the plane Π2).

    Quadrants are referred to as: I (upper front), II (upper back), III (lower back), IV (lower front).

    The half-space or quadrant of T(x,y,z) depends on the sign of the y and z coordinates (see table).
    half-spacez
    upper+
    lower−


    half-spacey
    front+
    back−


    quadrantyz
    I++
    II−+
    III− −
    IV+−


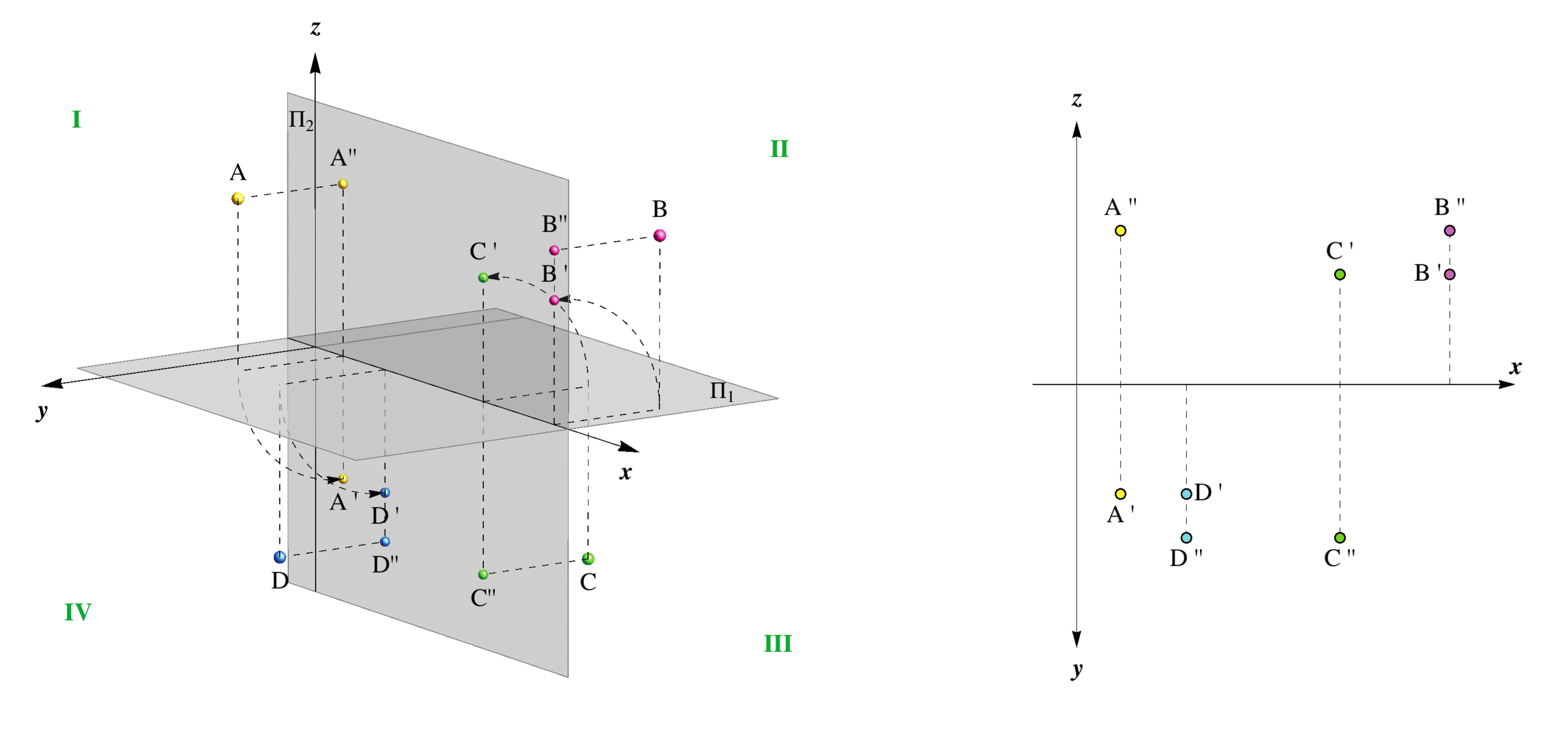
    From the horizontal and vertical projections of a point it can be determined to which quadrant it belongs.
    In the figure below are some examples of points in different quadrants and their orthogonal projections
    (A ∈ I, B ∈ II, C ∈ III, D ∈ IV).

    Points in special positions

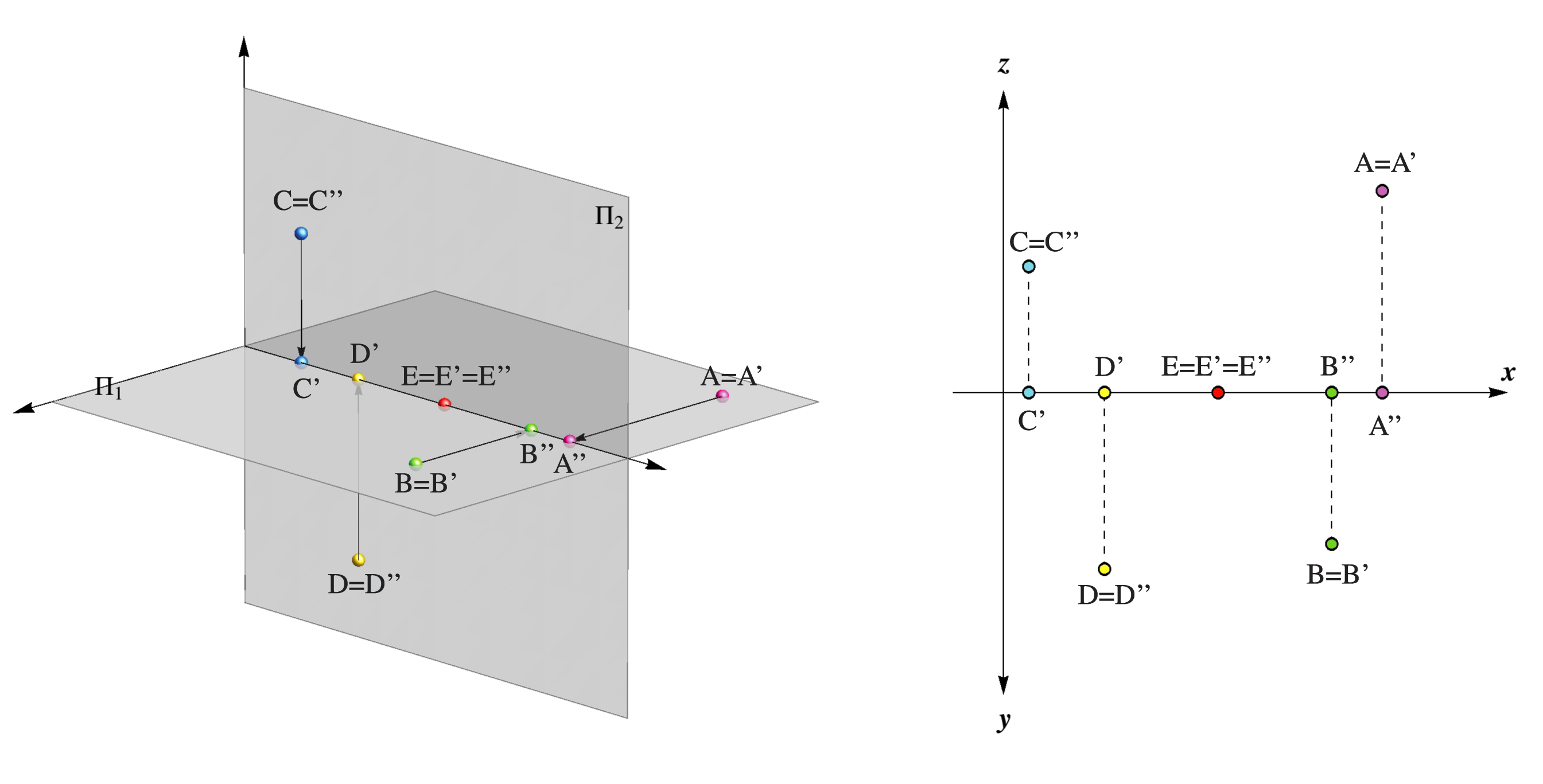
    If a point lies in one of the projection planes, then it will coincide with its projection onto that plane, while the other projection will lie on the x-axis.

  • If T ∈ Π1, then T' = T and T'' ∈ x, i.e. its vertical projection lies on the x-axis.

  • If T ∈ Π2, then T'' = T and T' ∈ x, i.e. its horizontal projection lies on the x-axis.

  • If T ∈ x, then it coincides with its horizontal and vertical projections, i.e. T = T' = T'' .

    On the following figure projections of the following points are shown: A,B ∈ Π1, C,D ∈ Π2 and E ∈ x.

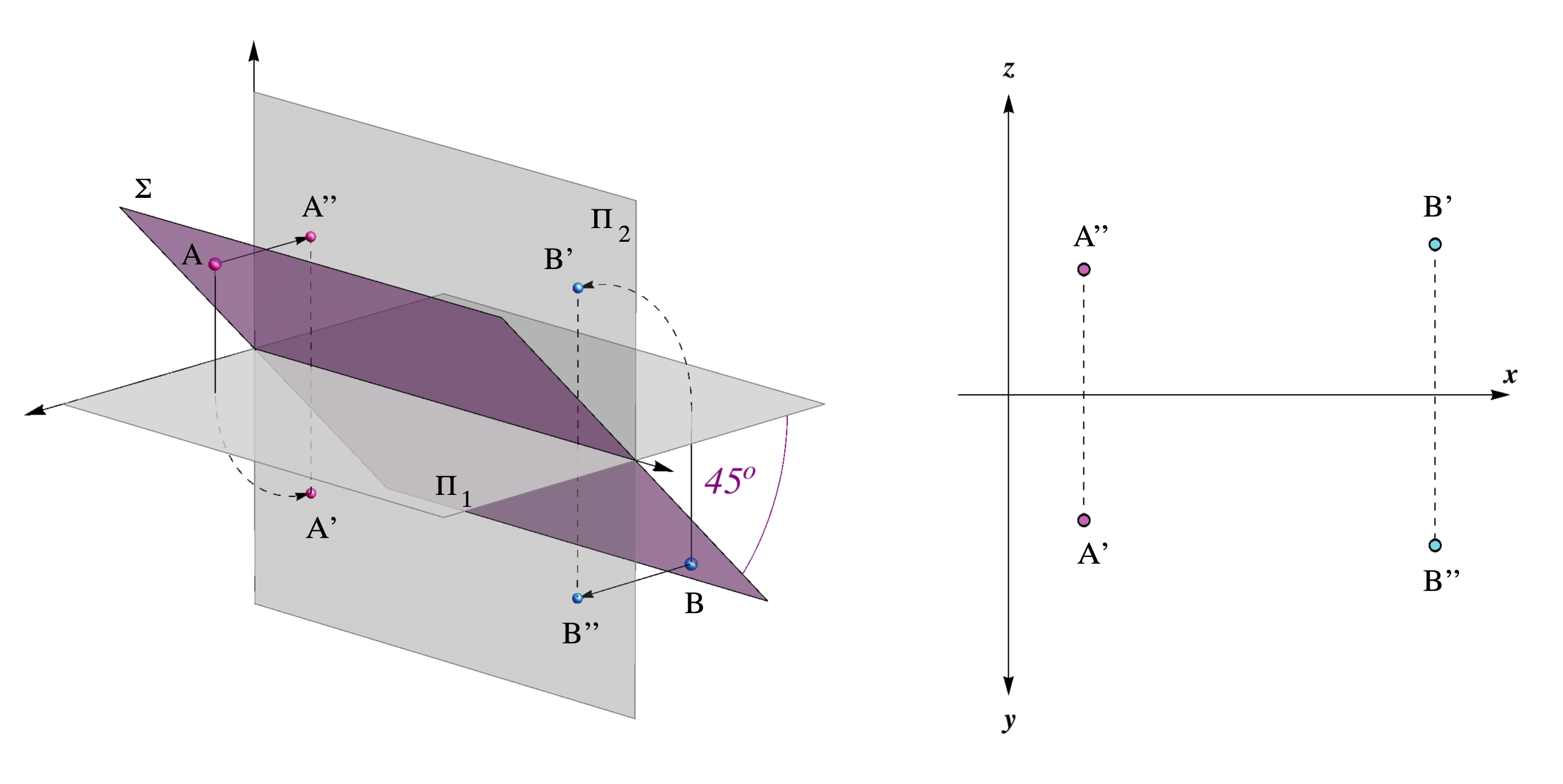
    Another two planes in space for which the horizontal and vertical projections are in a special position are:
  • Σ – symmetry plane, which bisects the Ist and IIIrd quadrant - the horizontal and vertical projections of every point are symmetrical around the x-axis.
  • Κ – coincidence plane, which bisects the IInd and IVth quadrant - the horizontal and vertical projections of every point coincide.

    On the figure below orthogonal projections of the two points A,B ∈ Σ are shown.
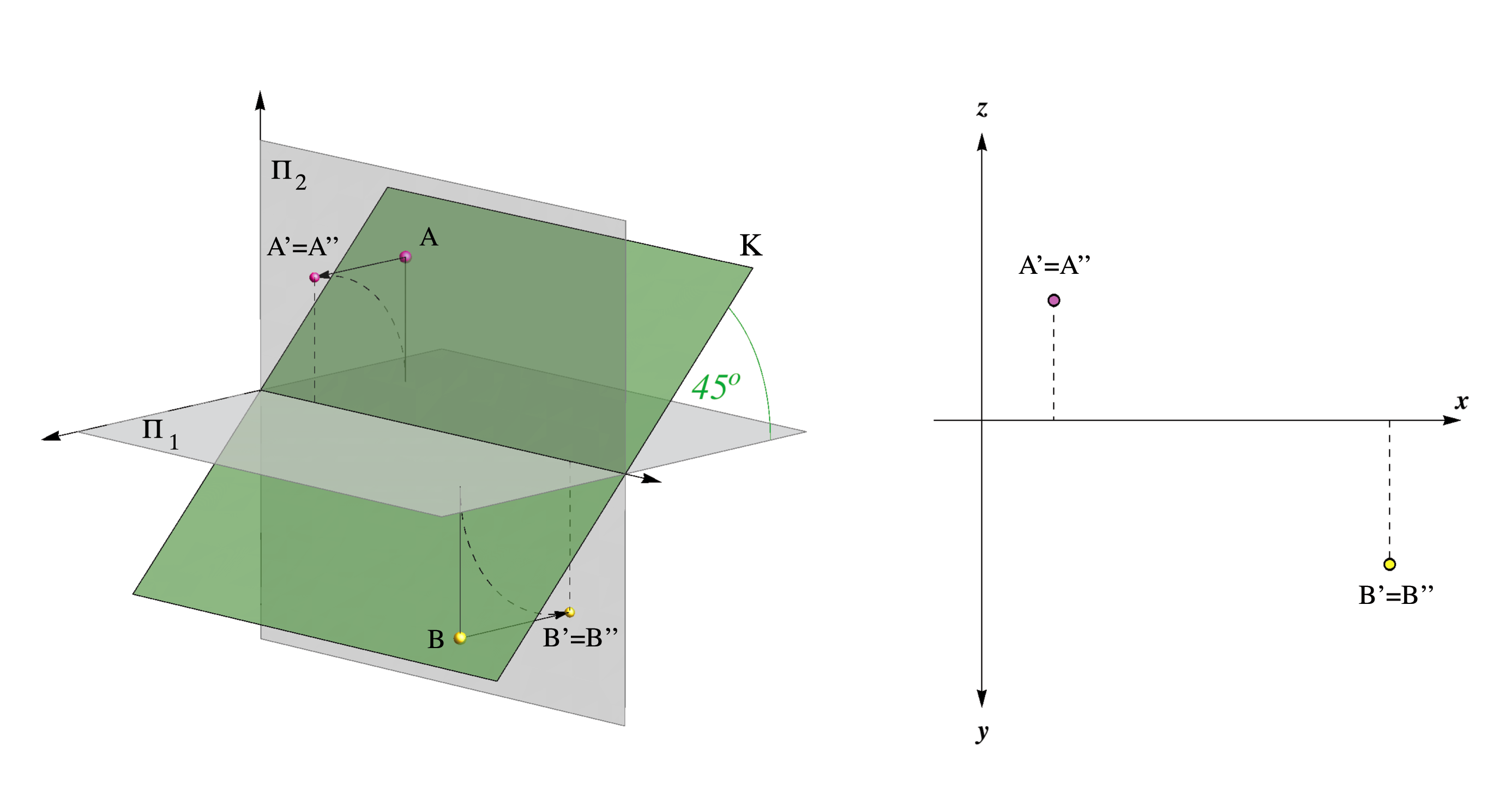
    On the figure below orthogonal projections of the two points A,B ∈ Κ are shown.



    Created by Sonja Gorjanc 3DGeomTeh - Developing project of the University of Zagreb.
    Translated by Helena Halas and Iva Kodrnja.