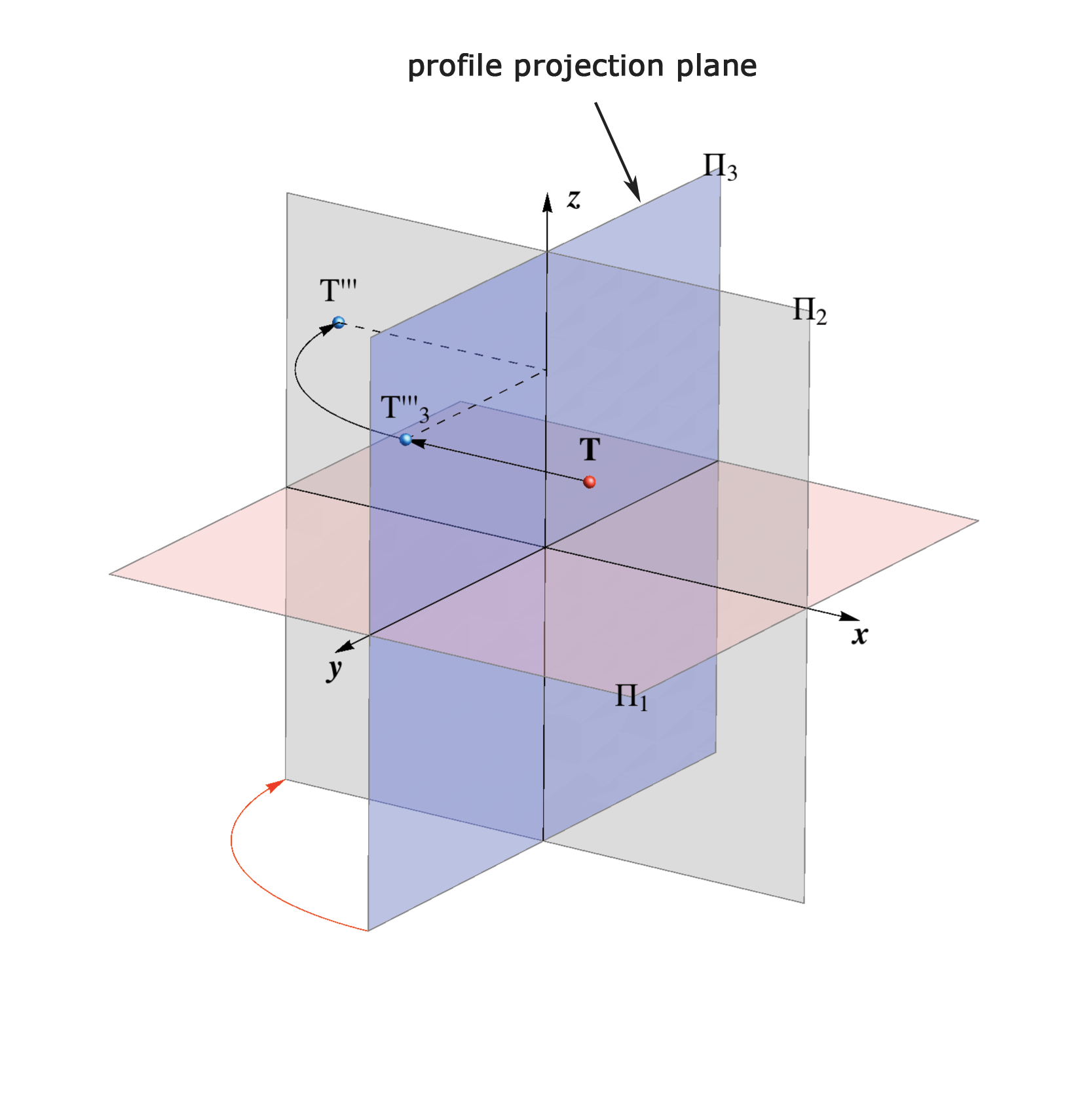
Profile Projection
Profile Projection of a Point
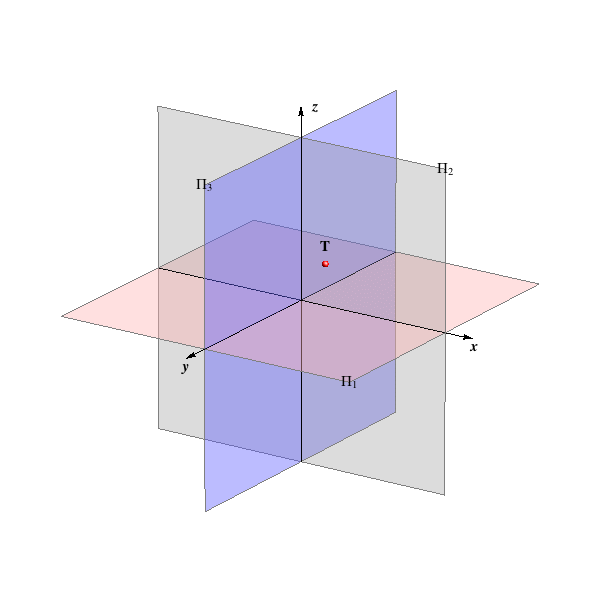
Let plane Π3 be determined by axes y and z.
In the left coordinate system O(x,y,z) the plane Π3 is called the
3rd projection plane or the profile projection plane.
Orthogonal projection of a point T on the plane Π3 is called the
3rd projection or the profile projection of the point T and is denoted with T'''3.
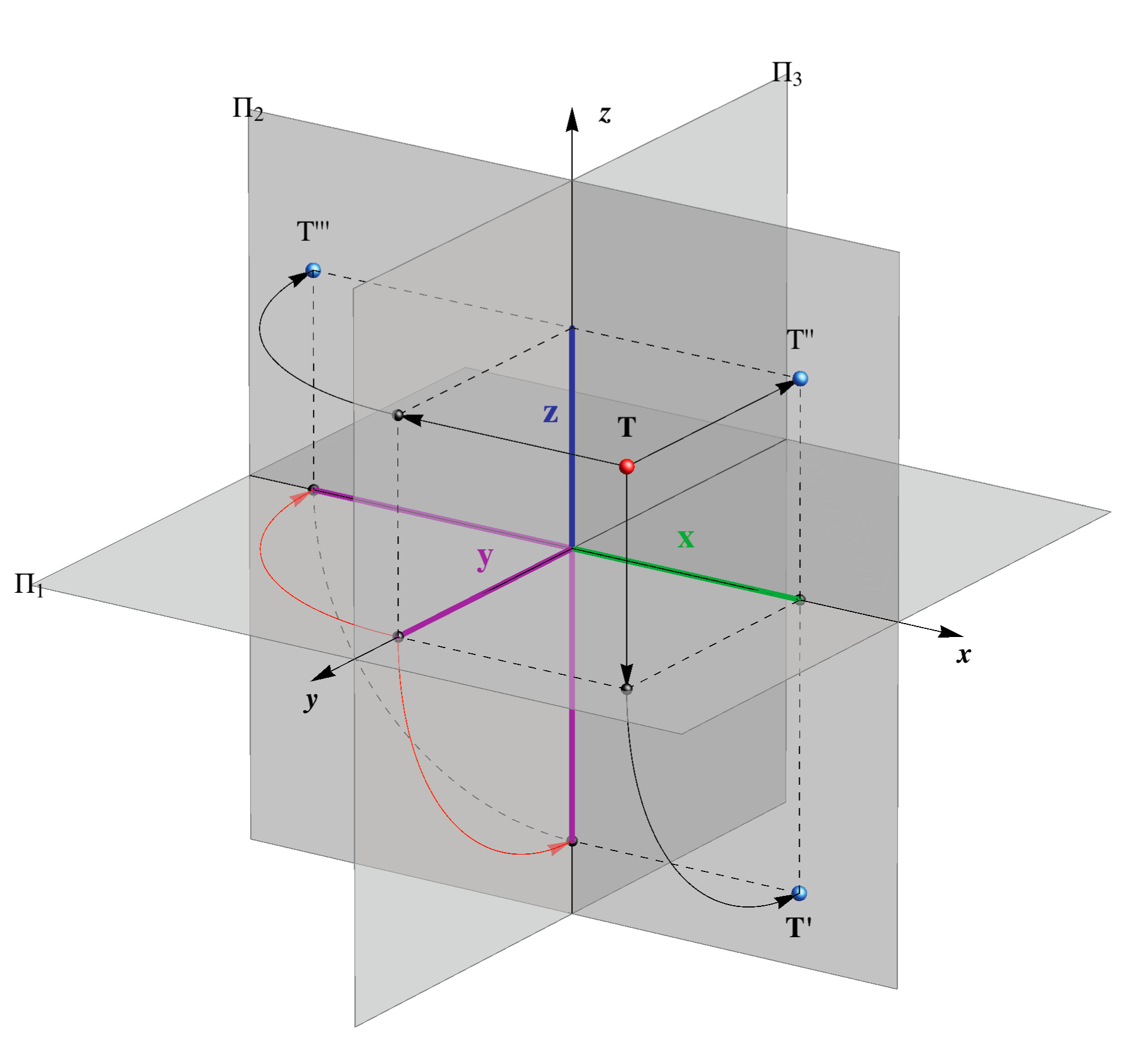
The plane Π3 is rotated clockwise around z-axis for 90o (left or negative rotation) into the drawing plane.
In this rotation the point T'''3 is mapped into the point T''' on the plane Π2.
The point T''' ∈ Π2 is also called the 3rd projection or the
left profile projection of a point T.
The right profile projection T''' ∈ Π2 is gained in the case of the right or positive rotation (counterclockwise) around the z-axis for 90o.
In the following, we will only observe the left profile projection and therefore it will be simply be referred to as the profile projection.
|
 |
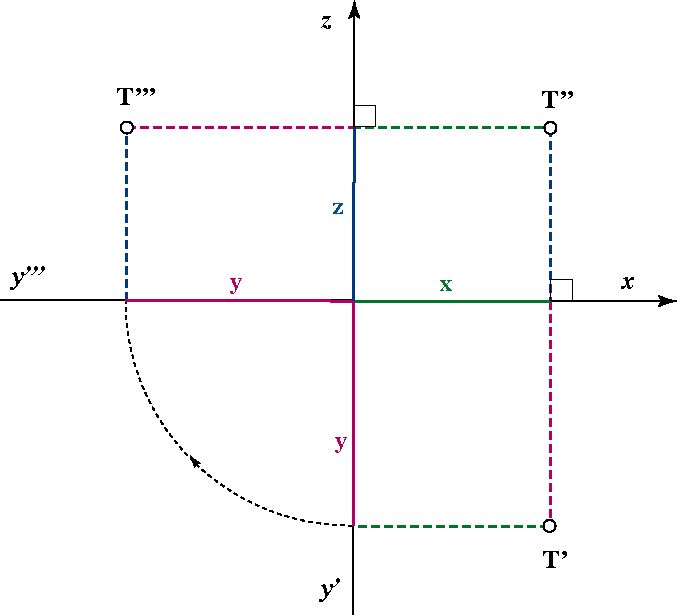
At this point we have three projections of a point T in the plane Π2 - its horizontal, vertical and profile projection (T',T'',T''').
The following animated illustration and picture represents the described procedure for gaining those three projections of a point in the plane Π2 and connections between certain projections.
|
Click on the picture for animation HORIZONTAL P.+VERTICAL P.+PROFILE P.
|
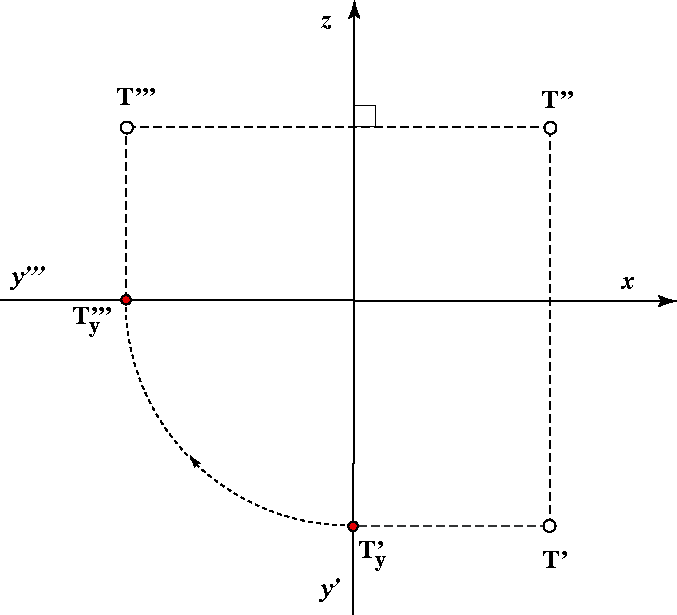
Projection of a point in the drawing plane.
|
The plane Π3 divides the space into two half-spaces — left and right.
View for the left profile projection is the view from the right side.
The planes Π1, Π2 and Π3 divide the space into eight octants.
Point T(x,y,z) belongs to a certain octant depending on the sign of the coordinates x, y and z (see table).
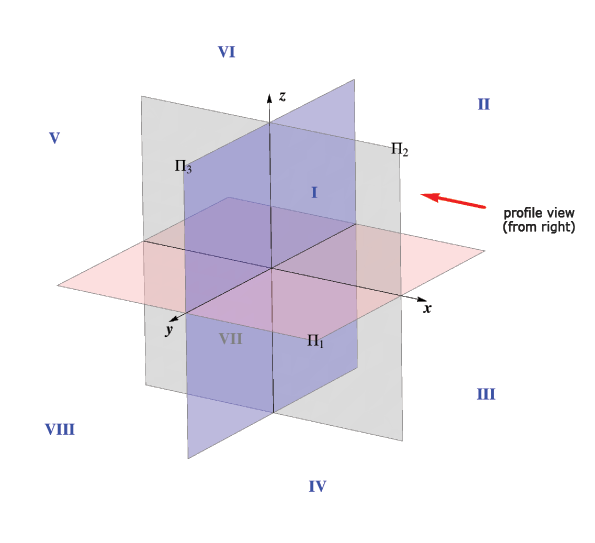 |
| octant | x | y | z |
| I | + | + | + |
| II | + | − | + |
| III | + | − | − |
| IV | + | + | − |
| V | − | + | + |
| VI | − | − | + |
| VII | − | − | − |
| VIII | − | + | − |
|
Profile projections of all points of the plane Π1 lie on the y-axis, (T ∈ Π1 <=> T''' ∈ y).
Profile projections of all points of the plane Π2 lie on the z-axis, (T ∈ Π2 <=> T''' ∈ z).
Horizontal and vertical projections of all points of the plane Π3 lie on the y and z-axis respectively (T ∈ Π3 <=> T' ∈ y & T'' ∈ z).
The distance of a point from the plane Π3 is determined by its x-coordinate:
d(T,Π3) = |x|,
for x > 0 point T lies on the right side of the plane Π3,
for x < 0 point T lies on the left side of the plane Π3.
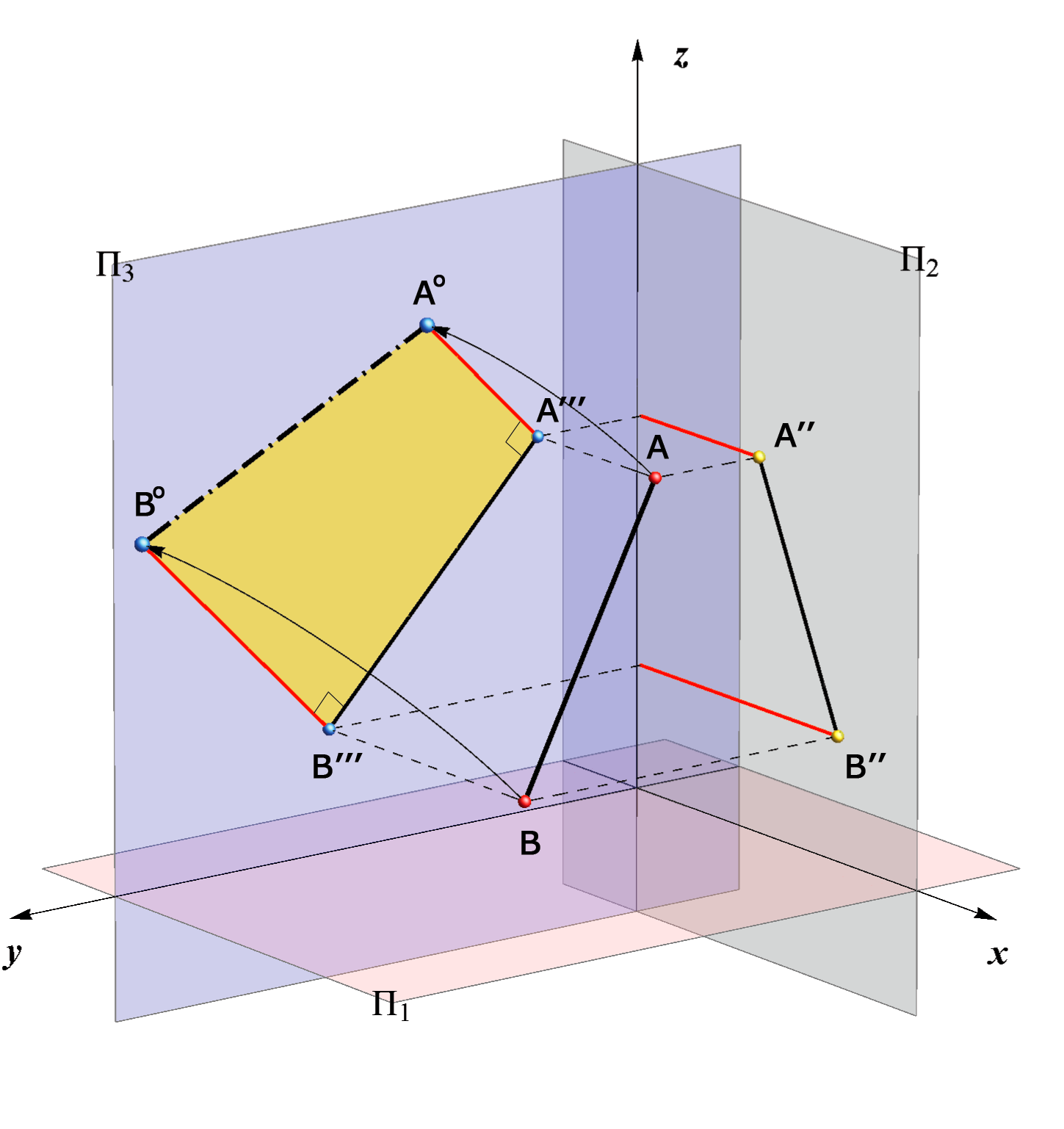
Determining the True Length of a Line Segment with the Profile Projection
The line segment Ao Bo in the plane Π3, for which is valid
d (Ao, Bo) = d (A,B), is constructed by the rotation of the trapezoid AA'''B'''B around the line A'''B''' for 90o.
This procedure is analogous to the procedure earlier explained for determining the true size using rotation into plane Π1 or Π2, wherein the length of the parallel edges of the trapezoid are determined by the x-coordinates of the points A and B.
If the sign of the x-coordinates of points A and B are different
(one point belongs to the left and other ro the right half-space) then the rotated positions we have two triangles instead of a trapezoid.
|
|
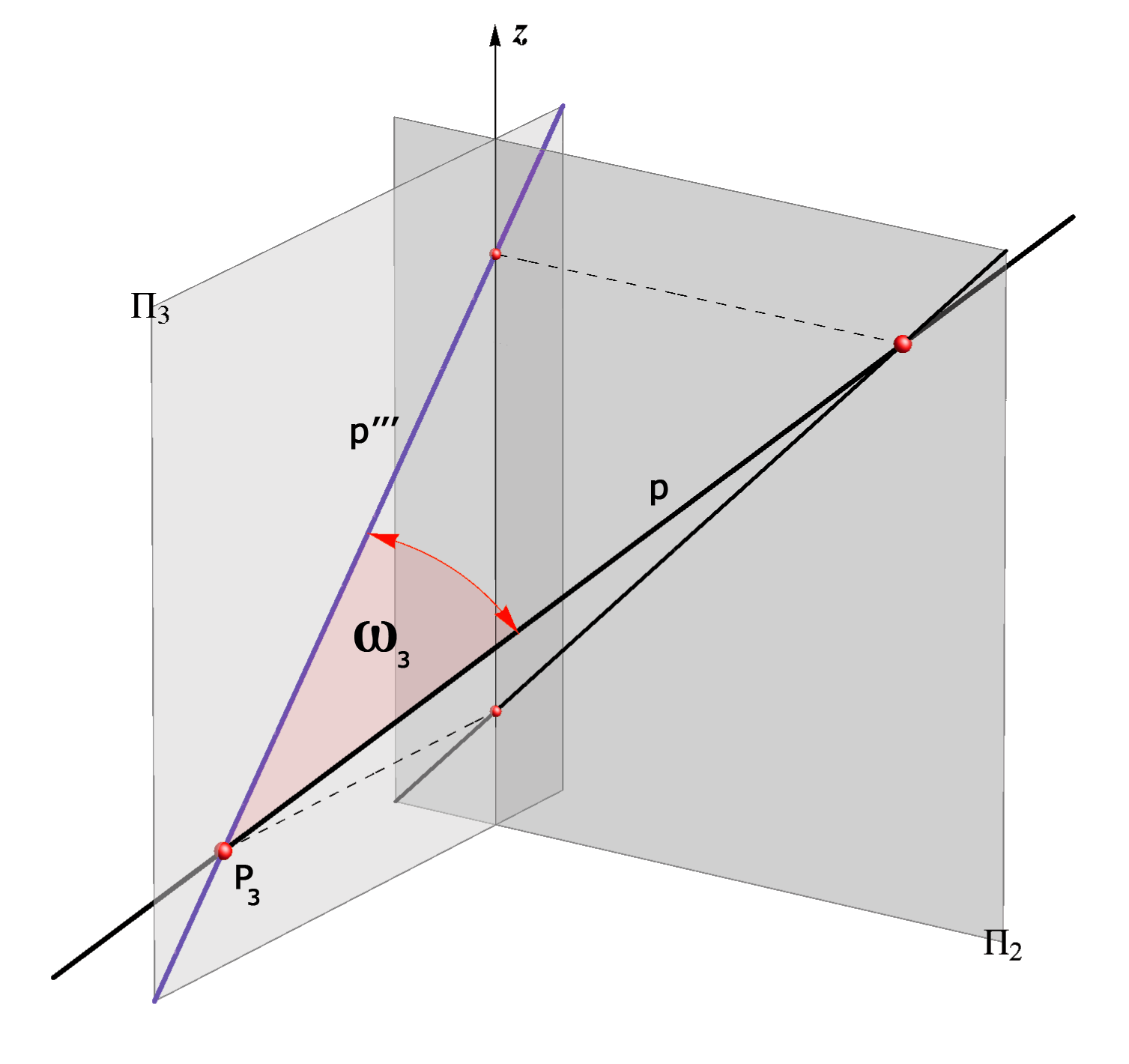
Profile Projection of a Straight Line
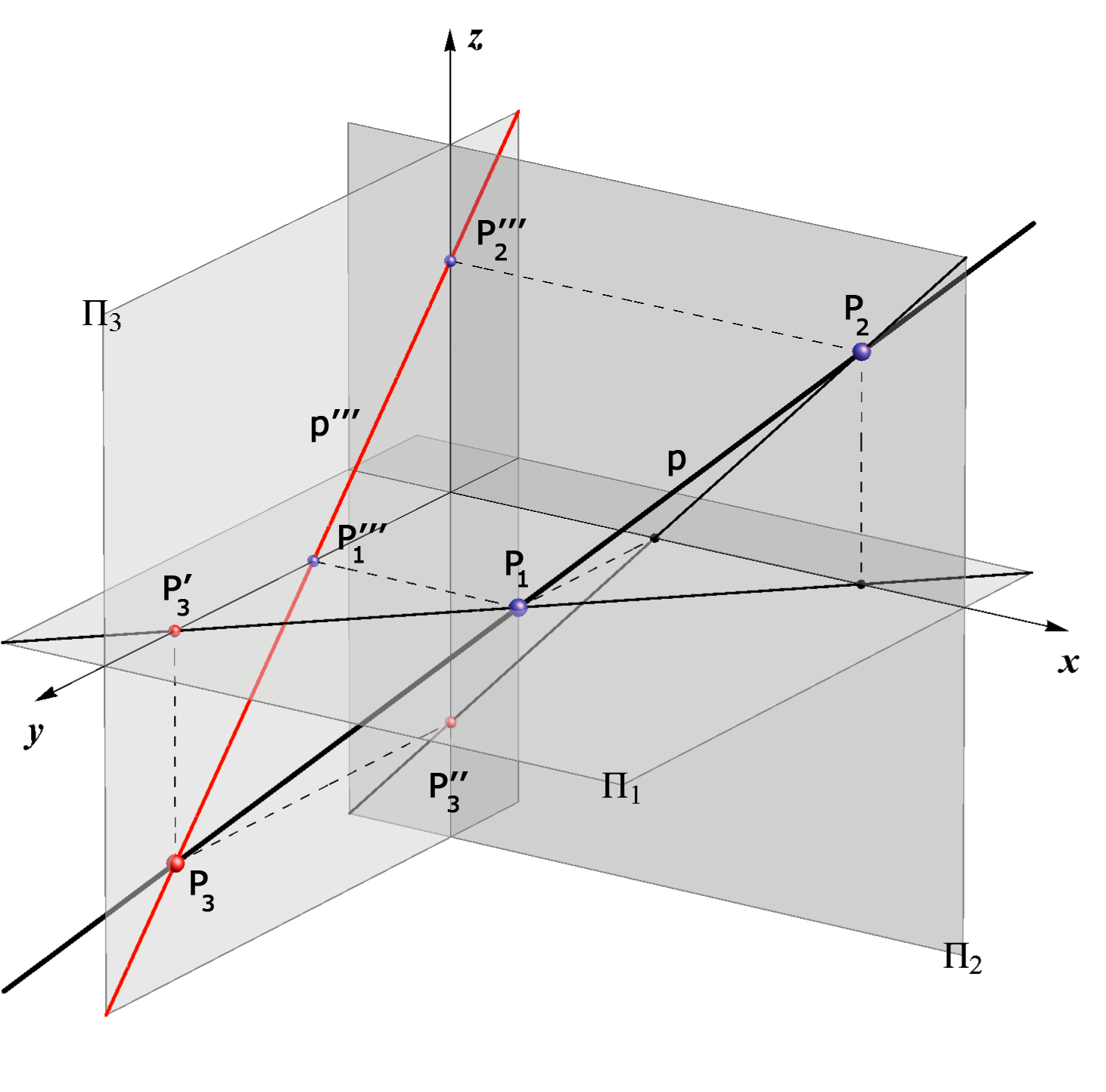
An arbitrary straight line p, not parallel to the x-axis has for the profile projection a straight line p'''.
Point P3 which is the intersection point of the straight line p and profile plane Π3 is called profile trace of the line p, P3 = p ∩ Π3.
The horizontal projection of this point lies on the y-axis and the vertical projection on the z-axis.
Profile projection of other traces of the line p, points P'''1 and P'''2, lie on the y or z-axis.
The third angle of inclination of a straight line p is the angle between the line and the profile plane, i.e. it is the angle between that line and its profile projection,
ω3 = ∠ (p, Π3) = ∠ (p, p''').
Special positions
Created by Sonja Gorjanc 3DGeomTeh - Developing project of the University of Zagreb.
Translated by Helena Halas and Iva Kodrnja.