2.2.8. Probodište pravca i ravnine

Probodište pravca i ravnine u općem položaju

U prethodnom smo poglavlju ustanovili da se u Mongeovom projiciranju položaj neke točke \(\small T\) u nekoj ravnini \(\small\mathrm P\)
određuje s pomoću bilo kojeg pravca te ravnine koji prolazi točkom \(\small T\).
Stoga ćemo pri konstrukciji probodišta \(\small P\) nekog pravca \(\small p\) s nekom ravninom \(\small\mathrm P\) (kad pravac ne leži u ravnini i nije s njom paralelan, a ravnina je u općem položaju prema ravninama projekcije) postupati tako da prvo odredimo takav pravac ravnine \(\small\mathrm P\) za koji znamo da se s pravcem \(\small p\) siječe upravo u njegovu probodištu s ravninom \(\small\mathrm P\).

Ta se konstrukcija svodi na provođenje sljedećeg postupka:

točka \(\small P\) sjecište pravaca \(\small p\) i \(\small f\) je traženo probodište.

Na animaciji 2.87 prikazana je vizualizacija tog prostornog postupka.

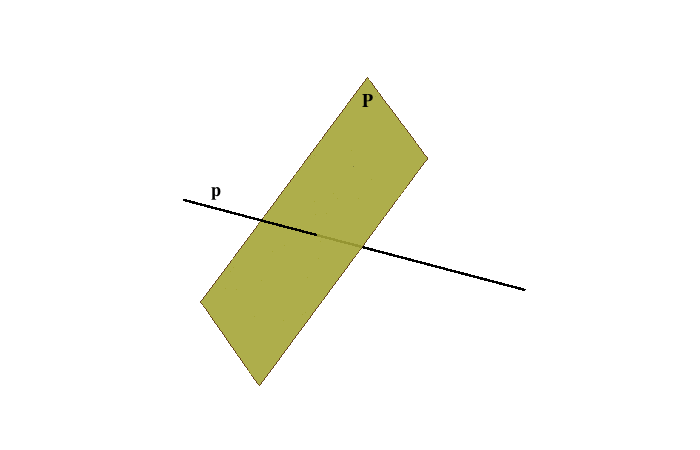
Slika 2.87 (klik na sliku za animaciju)

1. \(\Sigma,\,\,p\subset\Sigma\) 2. \( f=\mathrm p\cap\Sigma\) 3. \( P=p\cap f=p\cap\mathrm P\)

Kako se taj postupak provodi u Mongeovom projiciranju proučite preko sljedećih poveznica:

1. Probodište pravca i ravnine pomoću opće ravnine postavljene pravcem (Slika 2.88).

2. Probodište pravca i ravnine pomoću projicirajuće ravnine postavljene pravcem (Slika 2.89).

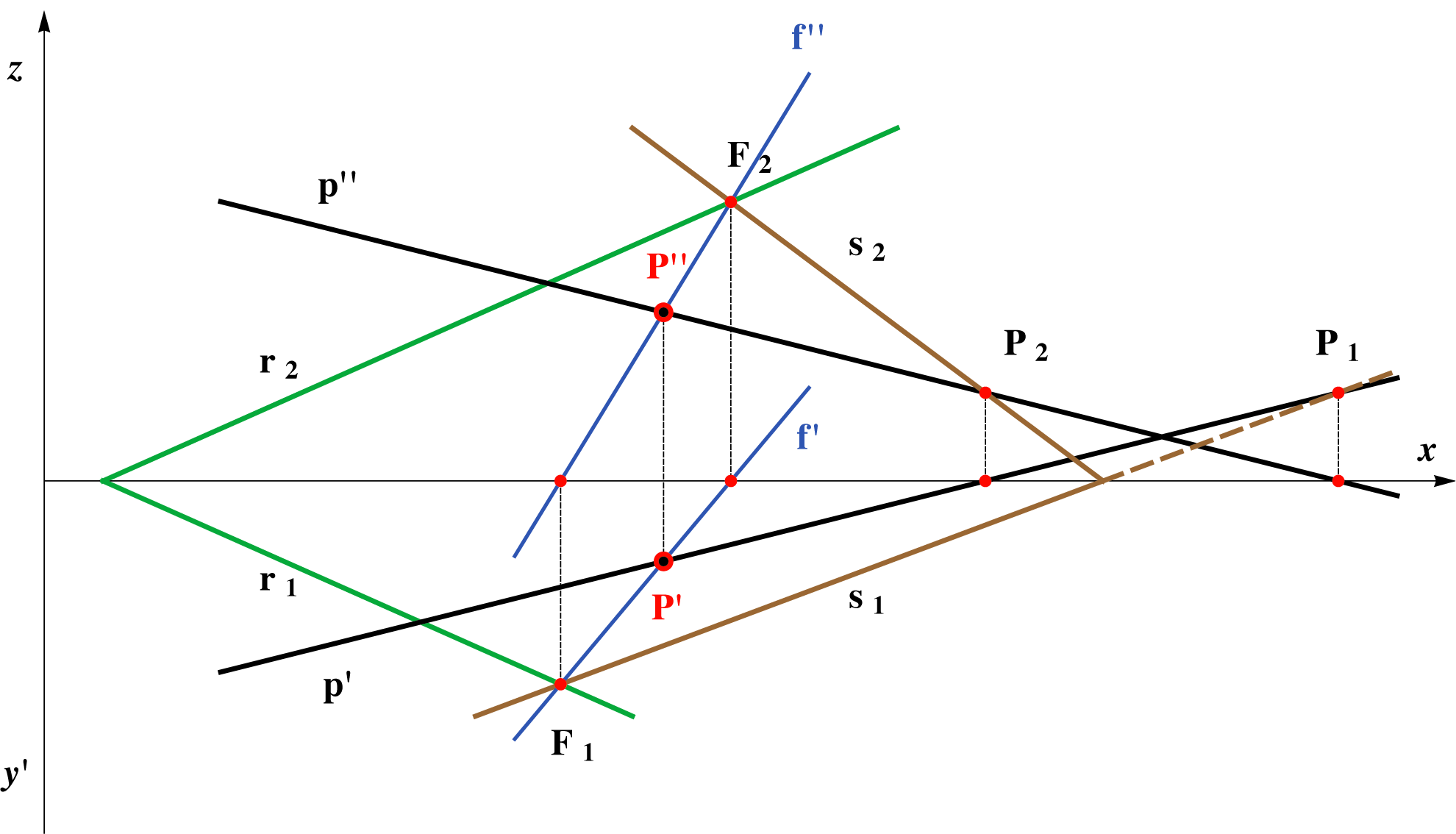
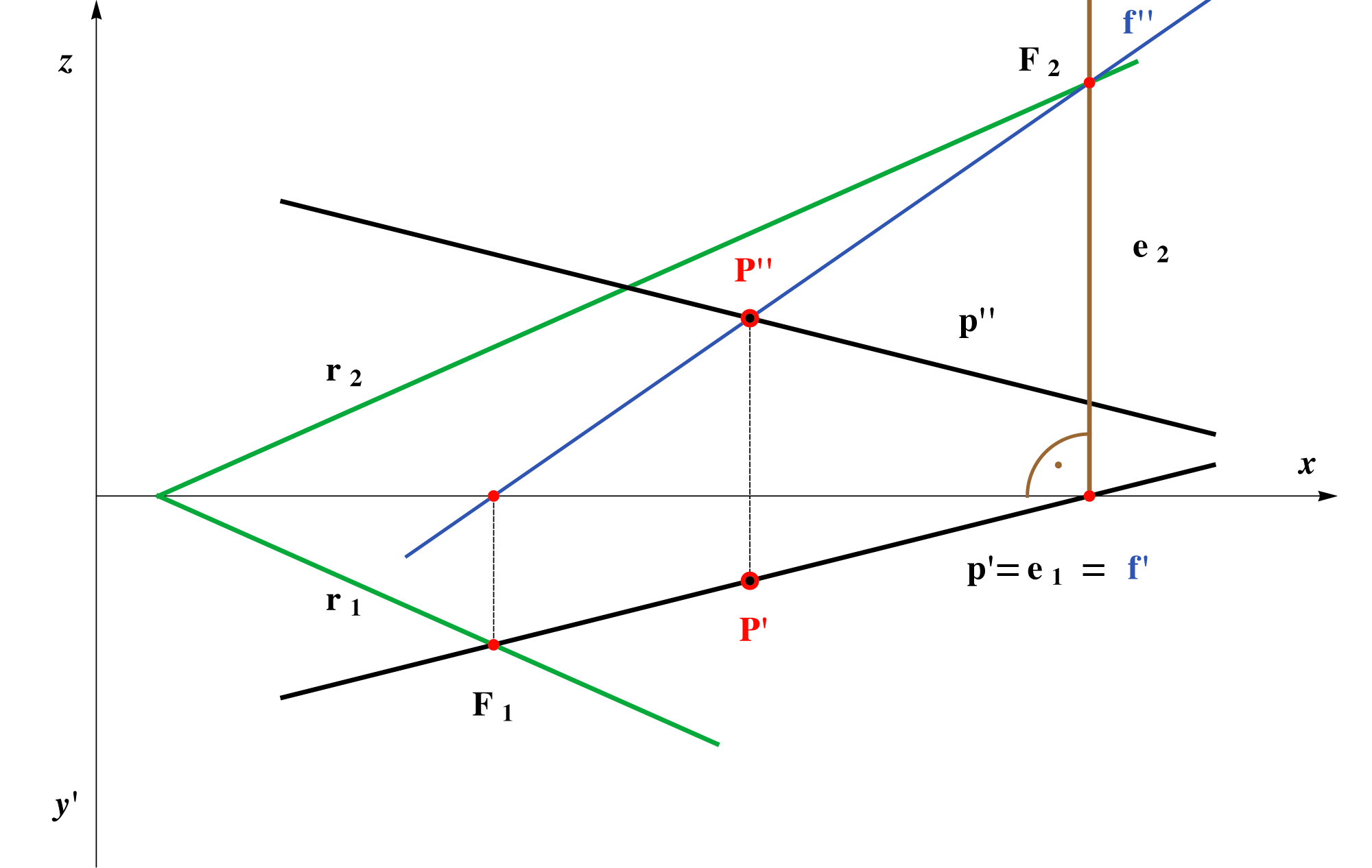
Usporedimo li te dvije konstrukcije (vidi slike 2.90a i 2.90b), jasno je zašto ćemo u provođenju postupka za konstrukciju probodišta pravca i ravnine pravcem postavljati uglavnom neku od projicirajućih ravnina.

Slika 2.90a: Pomoćna ravnina \(\small\Sigma\) je u općem položaju prema ravninama projekcije.	Slika 2.90b: Pomoćna ravnina \(\small\mathrm E\) je projicirajuća.

Zadatak 1: Konstruirajte tlocrt i nacrt probodišta pravca \(\small p=AB[A(0,5,3);B(6,-1,-1)]\) s ravninom \(\small \mathrm P(\infty,3,2)\).
Kao pomoćnu ravninu, pravcem \(\small p\) položite 2. projicirajuću ravninu \(\small \mathrm E\).
U obe projekcije naznačite vidljivost pravca \(\small p\) u odnosu na ravninu \(\small \mathrm P\).
RJEŠENJE (Slika 2.91)

Zadatak 2: Konstruirajte tlocrt i nacrt probodišta pravca \(\small a=A_1A_2[A_1(5,3,0);A_2(-1,0,4)]\) s ravninom \(\small \Delta (3,2,-3)\).
Kao pomoćnu ravninu, pravcem \(\small a\) položite 1. projicirajuću ravninu \(\small \mathrm E\).
U obe projekcije naznačite vidljivost pravca \(\small a\) u odnosu na ravninu \(\small \Delta\).
RJEŠENJE (Slika 2.92)

Probodište pravca s projicirajućom ravninom

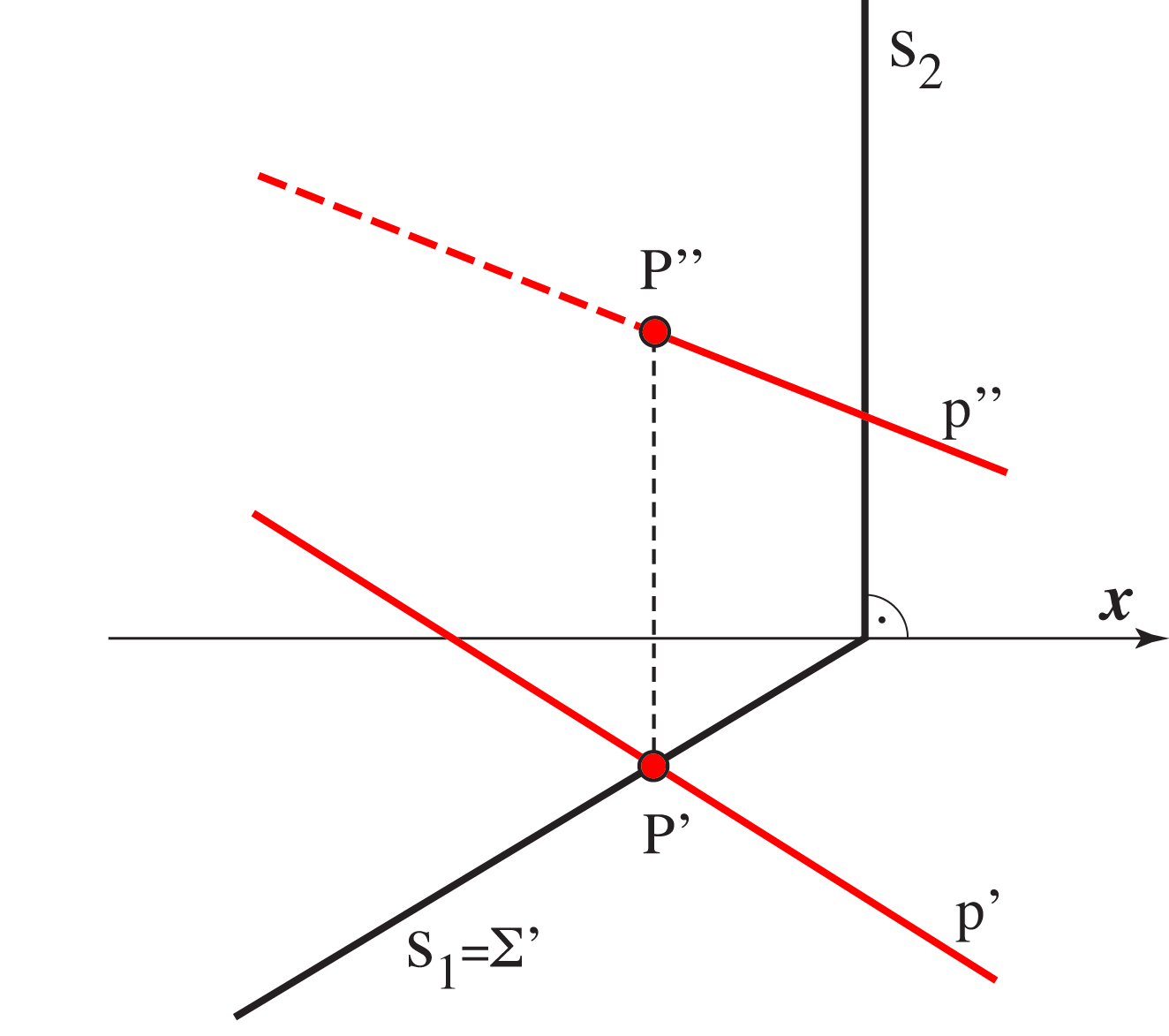
Gore navedene postupke nećemo trebati primjenjivati u slučajevima kada je ravnina s kojom tražimo probodište projicirajuća.
Naime, tada će se u jednoj projekciji (u onoj za koju je ta ravnina projicirajuća) cijela ravnina projicirati u svoj trag,
pa će se i probodište nekog pravca a s tom ravninom u toj projekciji projicirati na taj trag ravnine.
Vidi slike 2.93a i 2.93b.

Slika 2.93a: Konstrukcija probodišta pravca \(\small p\) i 1. projicirajuće ravnine \(\small \Sigma\).	Slika 2.93b: Konstrukcija probodišta pravca \(\small p\) i 2. projicirajuće ravnine \(\small \Sigma\).

Sonja Gorjanc - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu