2.2.9. Okomitost u Mongeovom projiciranju

PONOVITE osnovne definicije i teoreme vezane za okomitost.

Ortogonalna projekcija okomitih pravaca

Već smo prije istaknuli da se veličina kuta između pravaca NE čuva pri ortogonalnom projiciranju, pa stoga vrijedi:

  • Ortogonalne projekcije dva okomita pravca, koji su u općem položaju prema ravnini projekcije, NISU okomiti pravci.

    Kao i svaki drugi kut, i pravi će se kut ortogonalno projicirati u pravoj veličini ako su mu krakovi paralelni s ravninom projekcije.

    Međutim, za razliku od ostalih kutova, za pravi kut vrijedi i sljedeće:

  • Pravi se kut projicira ortogonalno u pravoj veličini ako mu je jedan krak paralelan s ravninom projekcije.

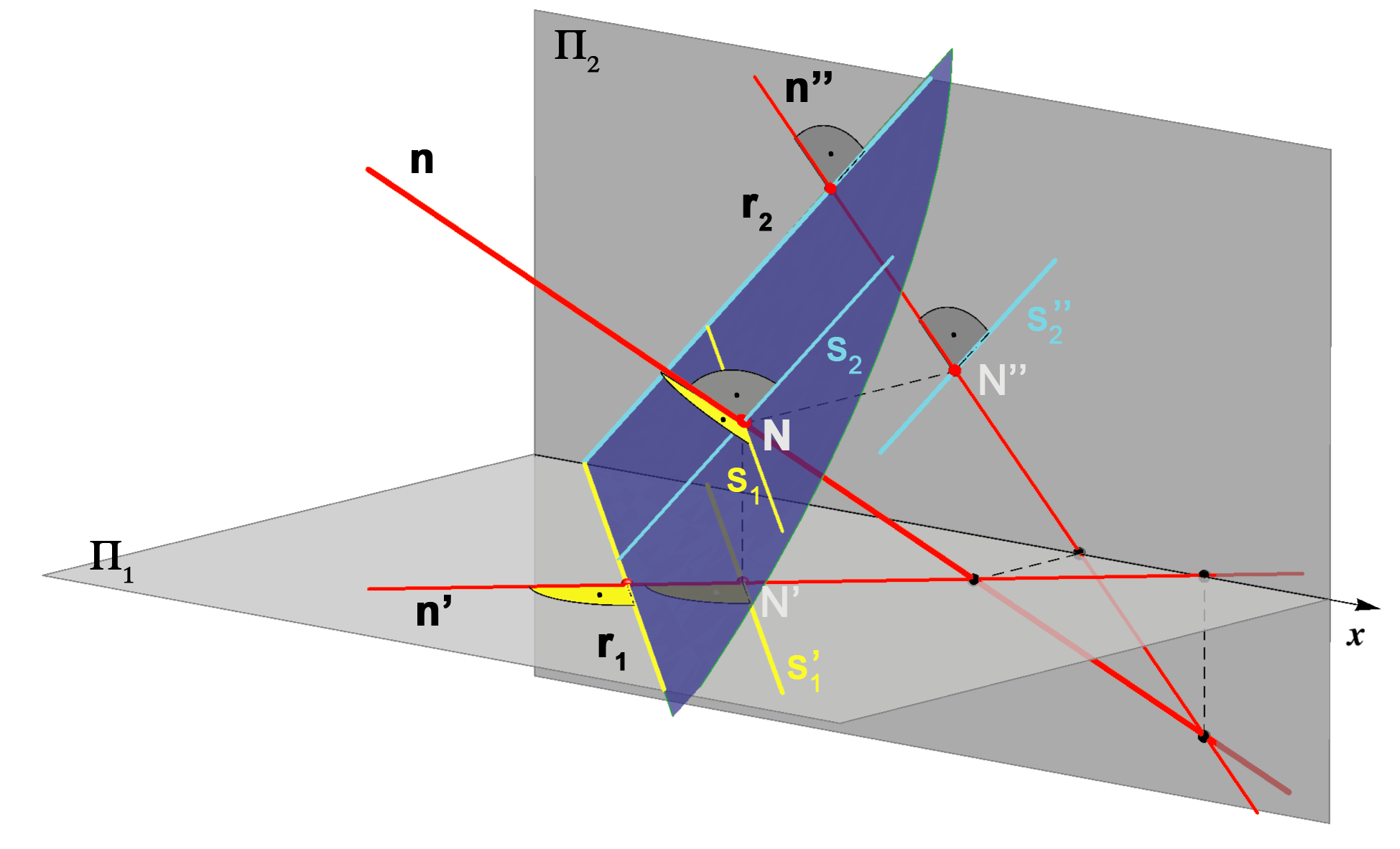
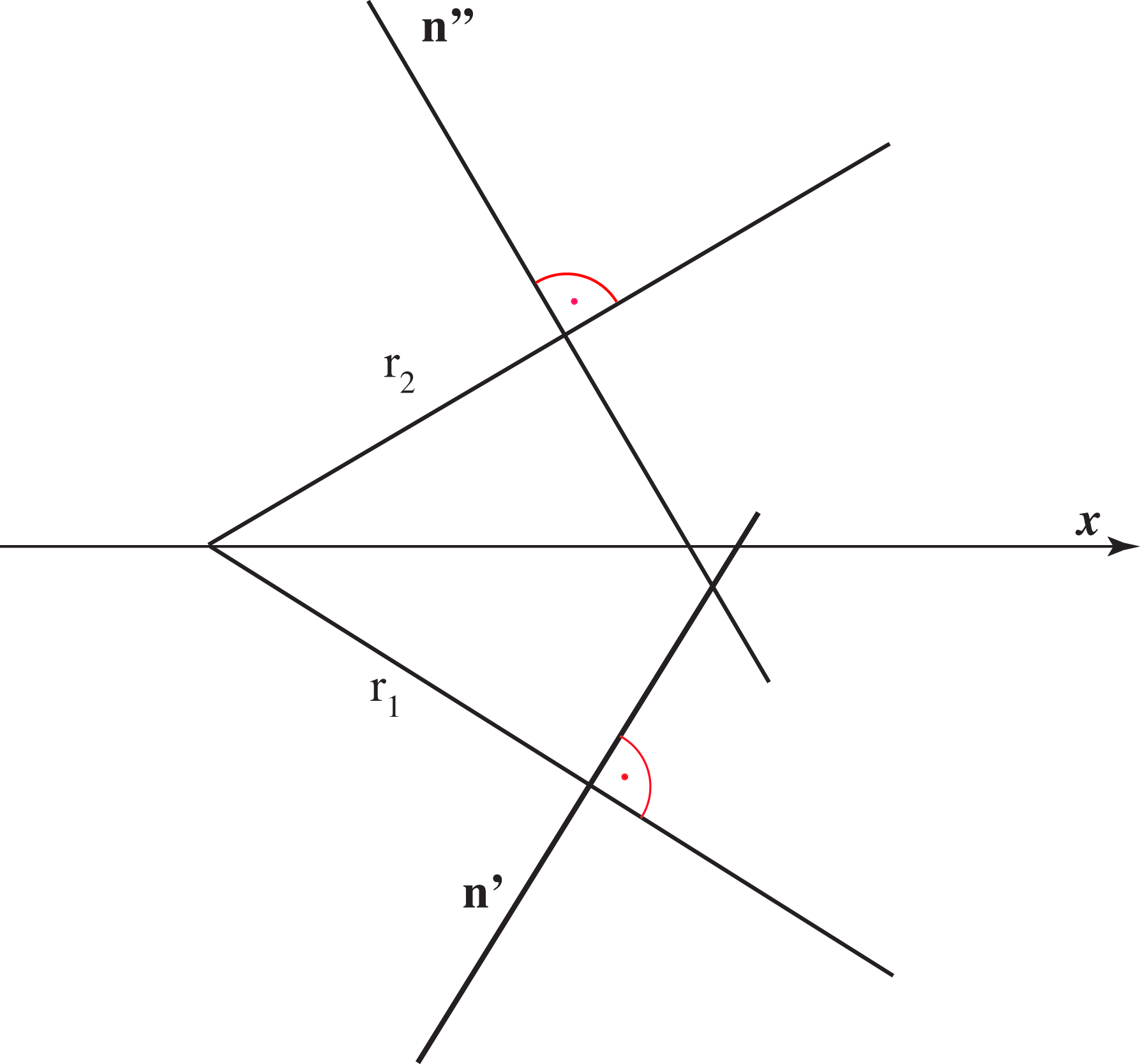
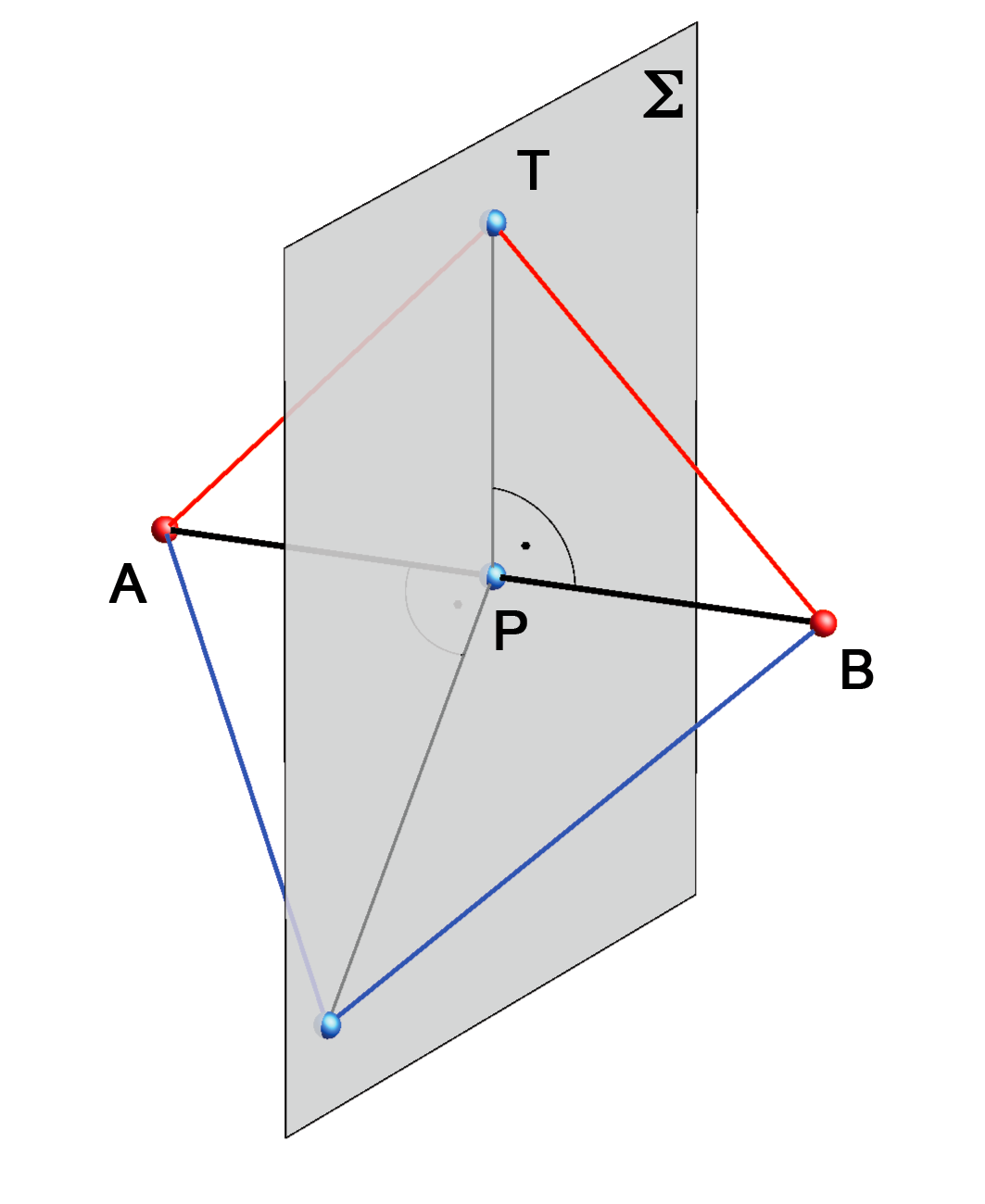
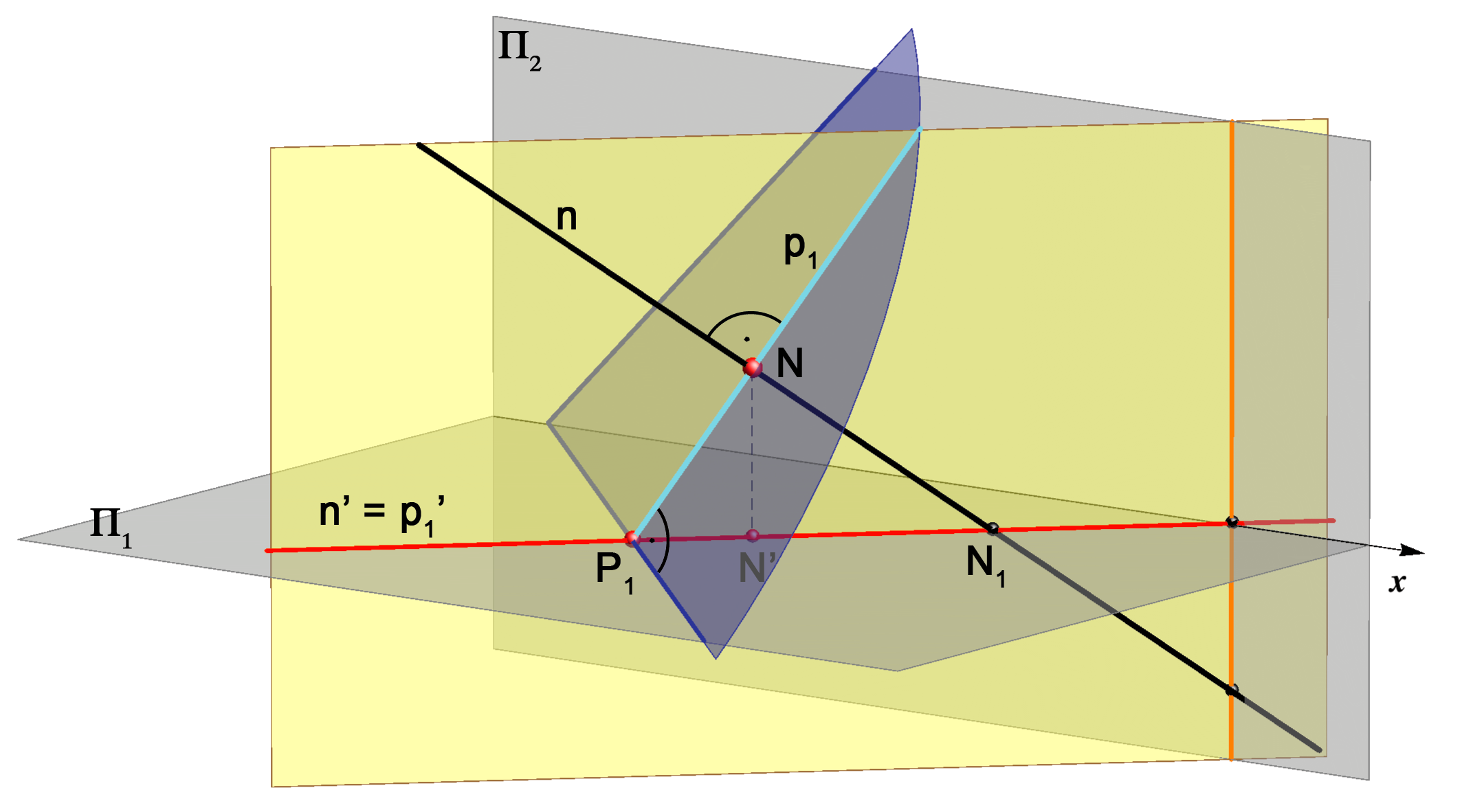
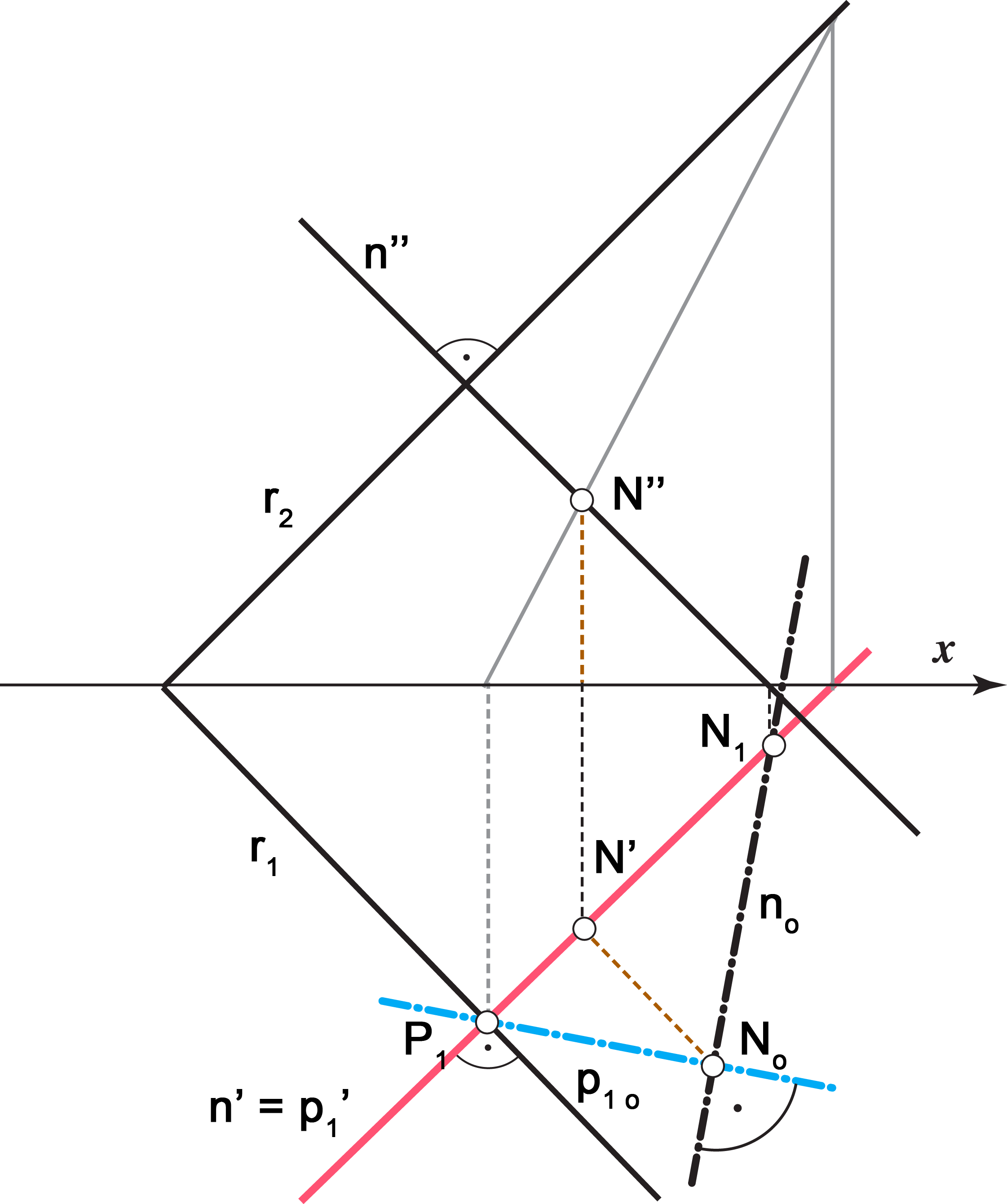
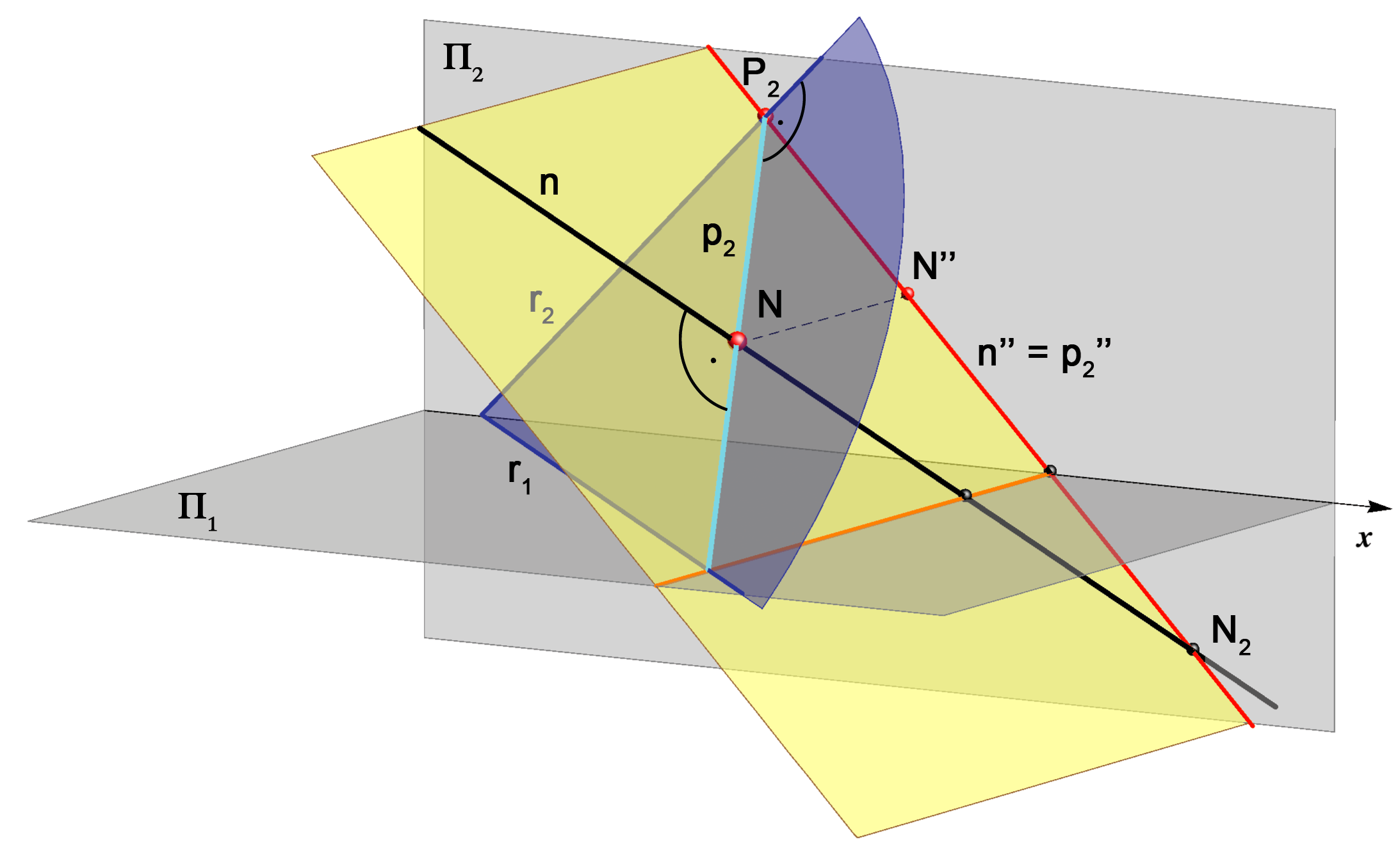
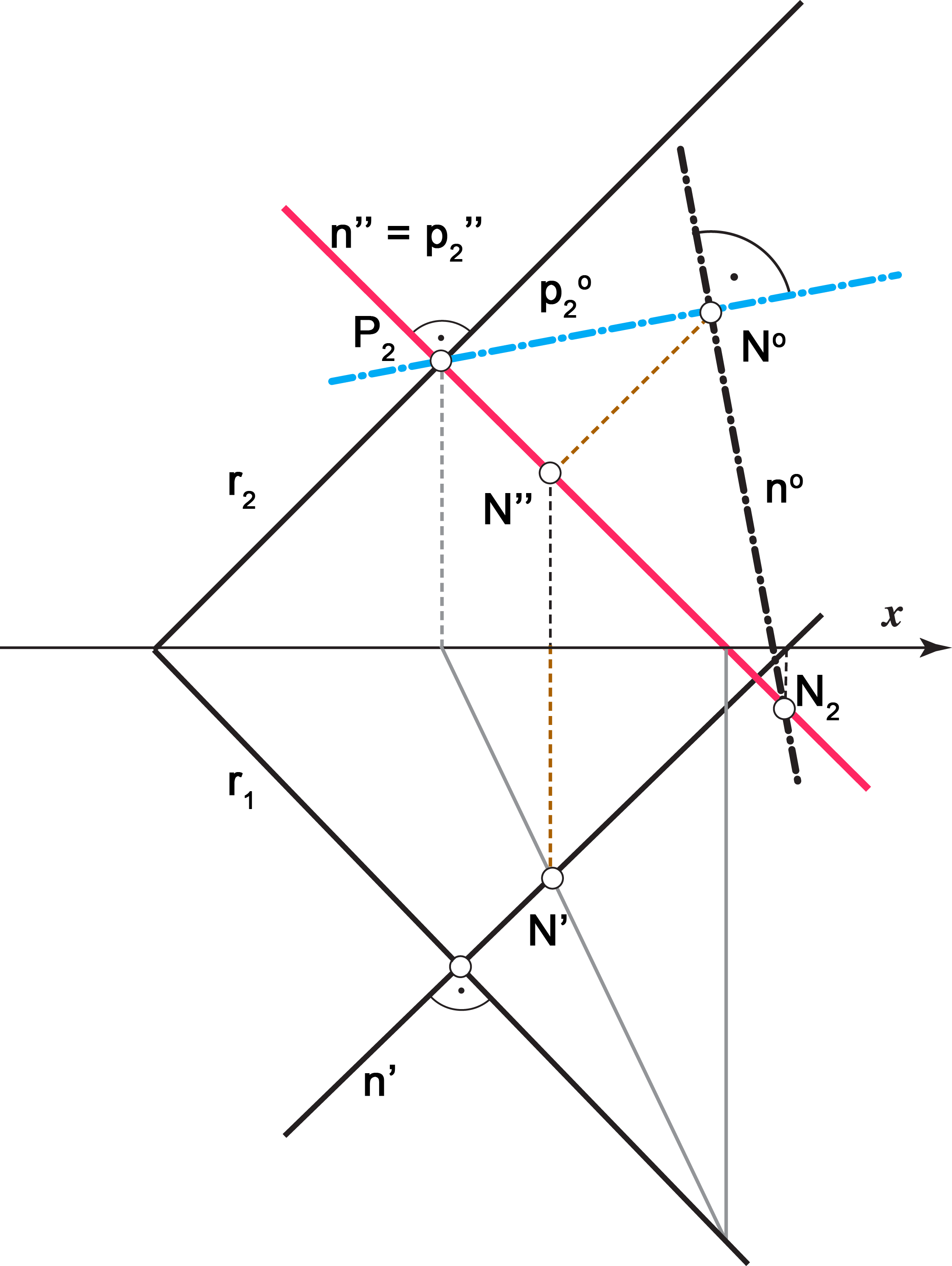
    Dokaz ove tvrdnje lako s prati uz sliku 2.94.
    Slika 2.94
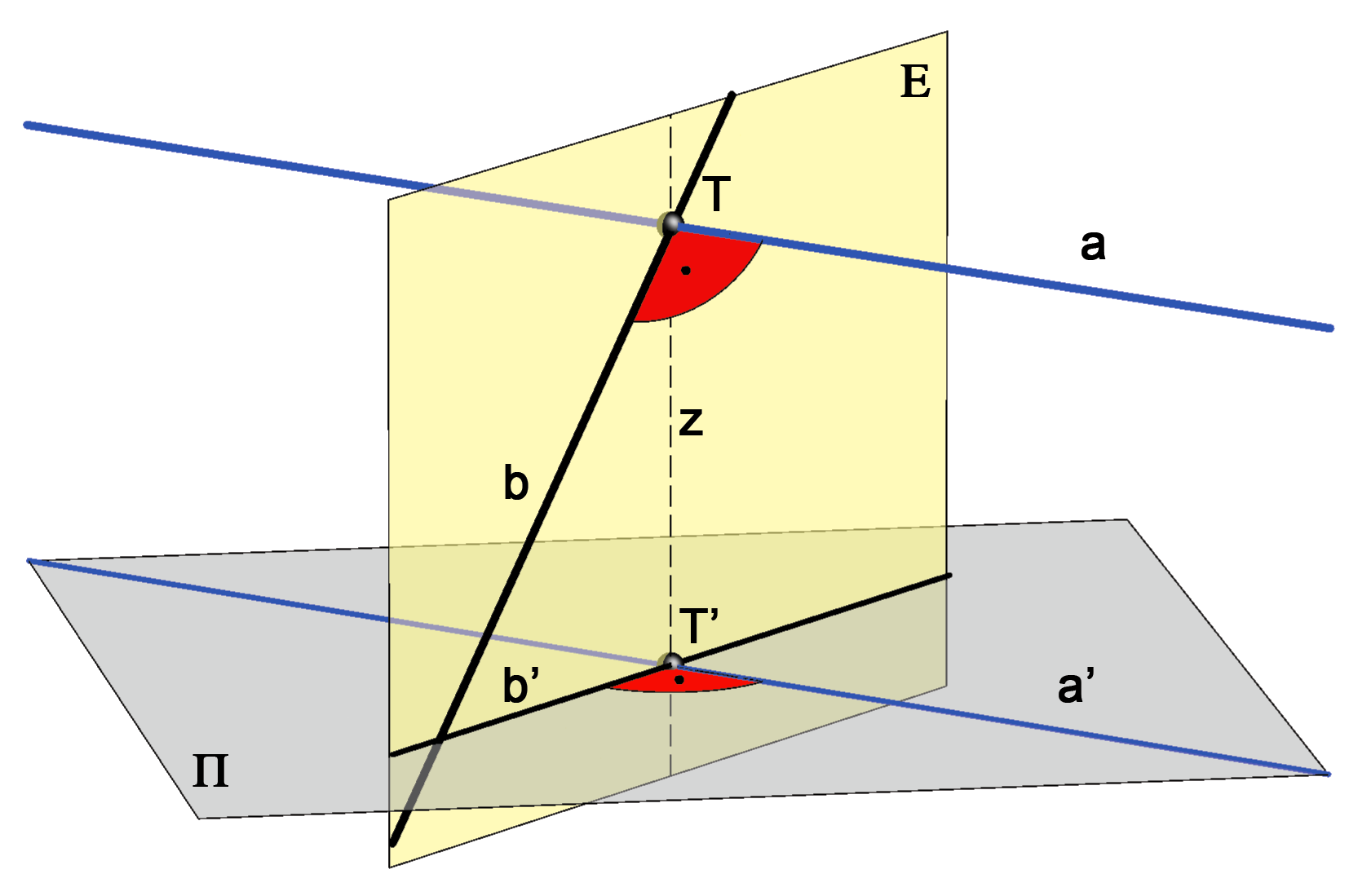
    		 Pravac \(\small a\) je paralelan s ravninom projekcije \(\small\Pi\) i okomit na pravac \(\small b\). Treba dokazati da su tada otogonalne projekcije tih pravaca također okomite, odnosno da je \(\small a'\perp b'\).

  • Pravac \(\small a\) okomit je na projicirajuću ravninu \(\small\mathrm E\) koja prolazi pravcem \(\small b\). Naime, \(\small a\) je okomit na dva pravca te ravnine: na pravac \(\small b\) i na zraku projiciranja \(\small z\)
    (okomit je na \(\small z\) jer je paralelan s ravninom \(\small\Pi\), a projiciranje je ortogonalno.)
  • Kako je pravac \(\small a'\) paralelan s pravcem \(\small a\), slijedi da je i okomit na ravninu \(\small\mathrm E\). Dakle, \(\small a'\) je okomit na sve pravce ravnine \(\small\mathrm E\), pa i na pravac \(\small b'\).

    Ovaj dokaz možemo kraće zapisati na sljedeći način:
    \(\small a\perp b\,\,\&\,\, a\parallel\Pi\,\,\,\Longrightarrow\,\,\,a\perp\mathrm E \,\,\,\Longrightarrow\,\,\, a'\perp\mathrm E\,\,\,\Longrightarrow\,\,\, a'\perp b'\).

    • Okomitost pravca i ravnine

    Pravac \(\small n\) koji je okomit na ravninu \(\small \mathrm P\) nazivamo okomicom ili normalom ravnine \(\small \mathrm P\), a probodište \(\small N=n\cap\mathrm P\) nazivamo nožištem normale \(\small n\).

  • Pravac \(\small n\) je okomit na ravninu \(\small \mathrm P\) ako i samo ako su njegove projekcije okomite na odgovarajuće tragove, odnosno

    \( n\perp\mathrm P\,\,\Longleftrightarrow \,\,p'\perp r_1\,\,\&\,\,p''\perp r_2.\)


    Gornja tvrdnja slijedi iz činjenice da je pravac koji je okomit na ravninu, okomit na sve pravce te ravnine, pa i na njezine tragove.
    Budući da je pravac okomit na trag \(\small r_1 (r_2)\) koji leži u ravnini \(\small \Pi_1(\Pi_2)\) taj će se pravi kut u tlocrtu (nacrtu) projicirati u pravoj veličini.

    Na slici 2.95, koja vizualizira to svojstvo, istaknute su i one sutražnice ravnine koje sijeku normalu \(\small n\), odnosno koje prolaze nožištem normale.

    Slika 2.95



    Zadatak 1: Konstruirajte projekcije pravca koji prolazi zadanom točkom, a okomit je na ravninu zadanu tragovima.

    Zadatak 2: Konstruirajte tragove ravnine koja prolazi zadanom točkom, a okomita je na zadani pravac. RJEŠENJE (Slika 2.96)

    Zadatak 3: Odredite udaljenost zadane točke od ravnine zadane tragovima. RJEŠENJE(Slika 2.97)

    Zadatak 4: Odredite udaljenost zadane točke od zadanog pravca. RJEŠENJE (Slika 2.98)

    Simetralna ravnina dužine


    Slika 2.99: \(\small T \in\Sigma\,\,\Longleftrightarrow \,\,d(A,T) = d(B,T)\)
  • Skup svih točaka prostora koje su jednako udaljene od krajnjih točaka neke dužine \(\small \overline{AB}\) leži u jednoj ravnini koju nazivamo simetralnom ravninom dužine \(\small \overline{AB}\).

  • Simetralna ravnina dužine \(\small \overline{AB}\) prolazi njezinim polovištem i okomita je na pravac \(\small AB\).







    		•


    Zadatak 5: Konstruirajte tragove simetralne ravnine dužine \(\small\overline {AB}[A(0,1,5);B(3,4,4)]\).


    Prevaljivanje normale

    Neka je pravac \(\small n\) okomit na ravninu \(\small \mathrm P\) i neka je točka \(\small N\) njihovo probodište.
    Neka je, nadalje, pravac \(\small p_1\) priklonica 1. skupine ravnine \(\small \mathrm P\) kroz točku \(\small N\), a pravac \(\small p_2\) priklonica 2. skupine iste ravnine koja također prolazi točkom \(\small N\).

    Zbog svojstva projiciranja okomice na ravninu (\(\small n'\perp r_1\), \(\small n''\perp r_2\)), jasno je da će se tlocrt pravca \(\small n\) podudarati s tlocrtom priklonice \(\small p_1\) (\(\small n' = p'_1\)),
    a nacrt pravca \(\small n\) s nacrtom priklonice \(\small p_2\) (\(\small n'' = p''_2\)).
    To znači da pravci \(\small n\) i \(\small p_1\) leže u istoj 1. projicirajućoj ravnini, dok \(\small n\) i \(\small p_2\) leže u istoj 2. projicirajućoj ravnini.

    Ta su svojstva prikazana na slikama 2.100 i 2.101.

    Slika 2.100a: Normala ravnine i priklonica 1. skupine kroz njezino nožište leže u istoj 1. projicirajućoj ravnini. Slika 2.100b: Normala prevaljena u \(\small \Pi_1\) okomita je na prevaljenu priklonicu 1. skupine, a siječe ju u prevaljenom nožištu.


    Slika 2.101a: Normala ravnine i priklonica 2. skupine kroz njezino nožište leže u istoj 2. projicirajućoj ravnini. Slika 2.101b: Normala prevaljena u \(\small \Pi_2\) okomita je na prevaljenu priklonicu 2. skupine, a siječe ju u prevaljenom nožištu.


    Zadatak 6: Iz točke \(\small T(1,3,-)\) ravnine \(\small \mathrm P(3,3,-5)\) uzdignite okomicu na tu ravninu duljine 4. RJEŠENJE (Slika 2.102)

    Okomitost dviju ravnina

    Dvije su ravnine okomite ako jedna od tih ravnina sadrži barem jedan pravac koji je okomit na drugu ravninu.

    Tada svaka od njih sadrži beskonačno mnogo pravaca (pramen paralelnih pravaca) koji su okomiti na drugu ravninu.

    U Mongeovom projiciranju okomitost dviju ravnina NE MOŽE se očitati iz položaja njihovih tragova, naime,
    njihovi odgovarajući tragovi NISU okomiti.
    Provjerite tu tvrdnju na nekom primjeru koji vam je lako zamisliti.

    Zadatak 7: Zadanim pravcem postavite ravninu koja je okomita na zadanu ravninu. RJEŠENJE (Slika 2.103)





    Sonja Gorjanc - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu