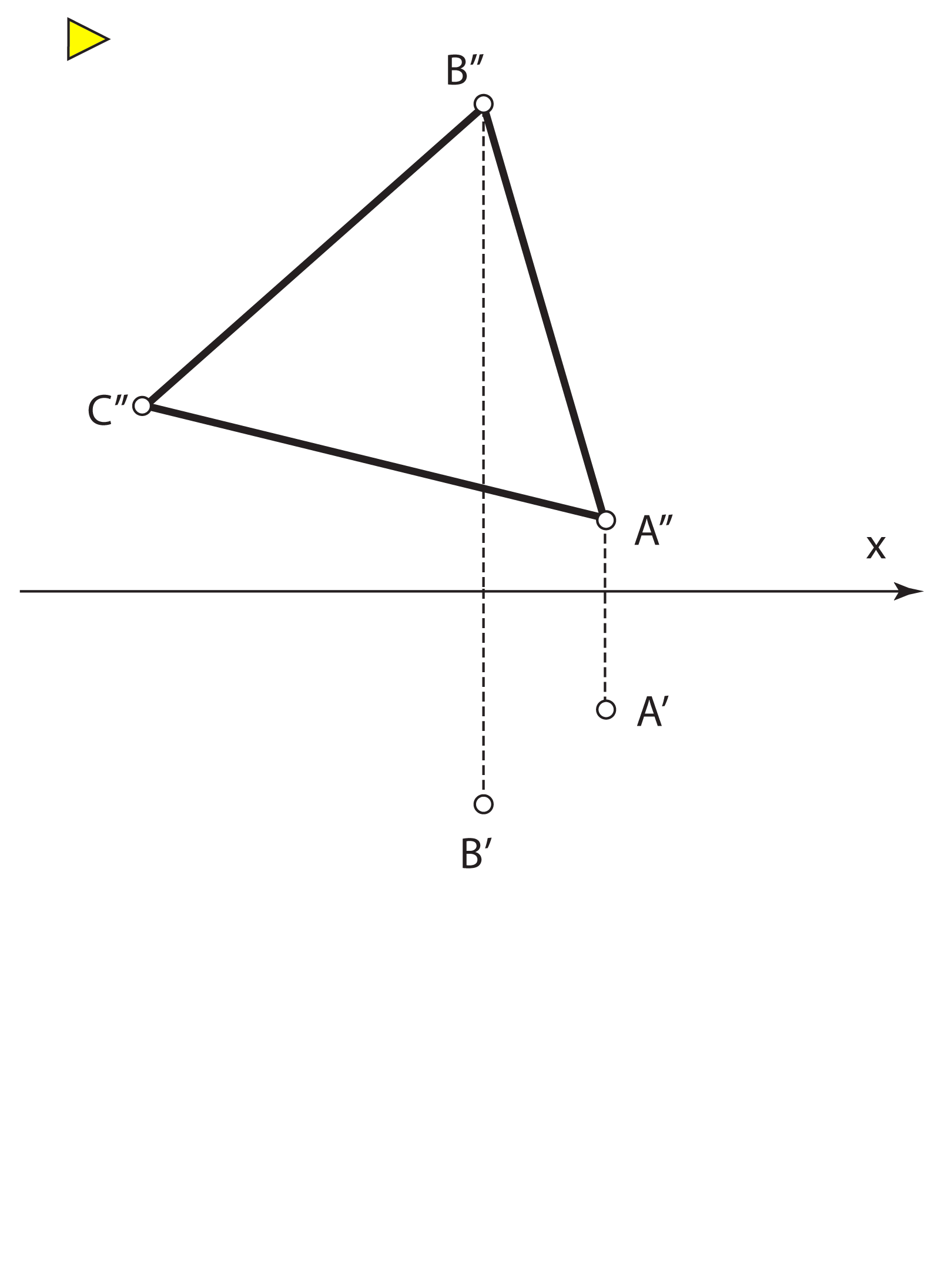
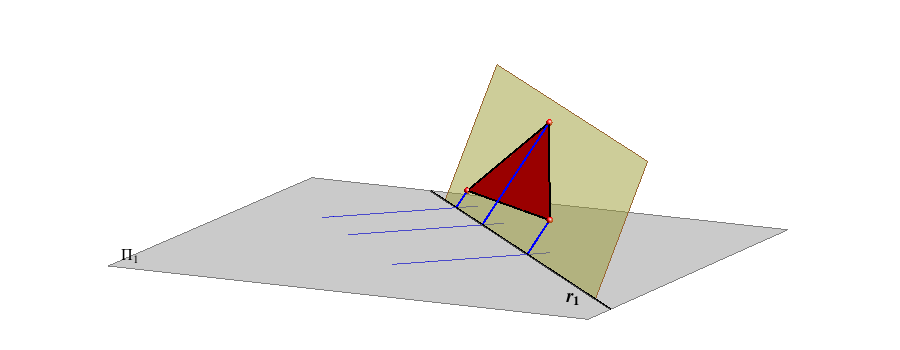
You should already be familiar with this procedure; it is called a revolution of a horizontal projecting plane.

|
You should already be familiar with this procedure; it is called a revolution of a horizontal projecting plane. |
|
|
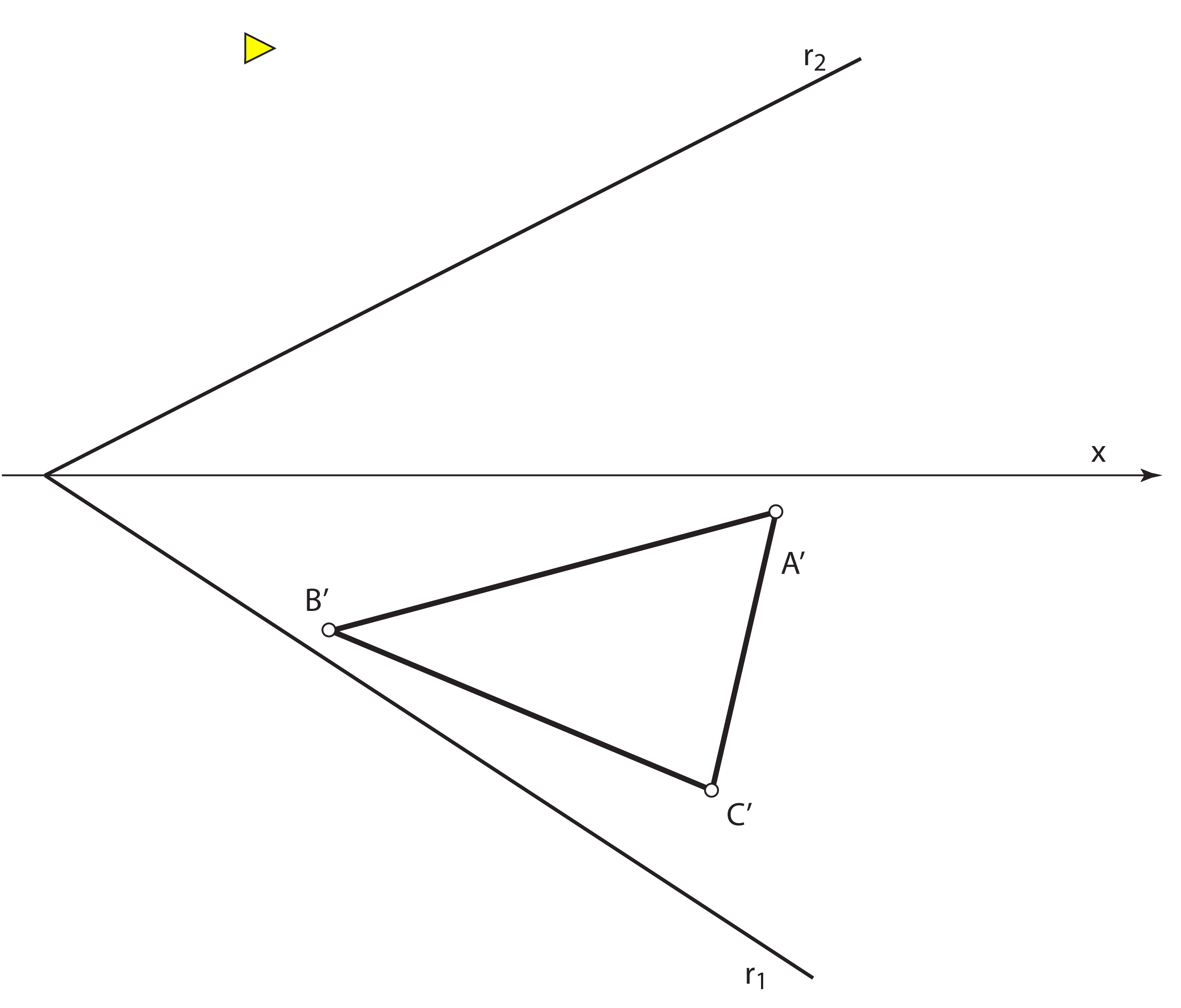
Click on the image to start the animation |
|
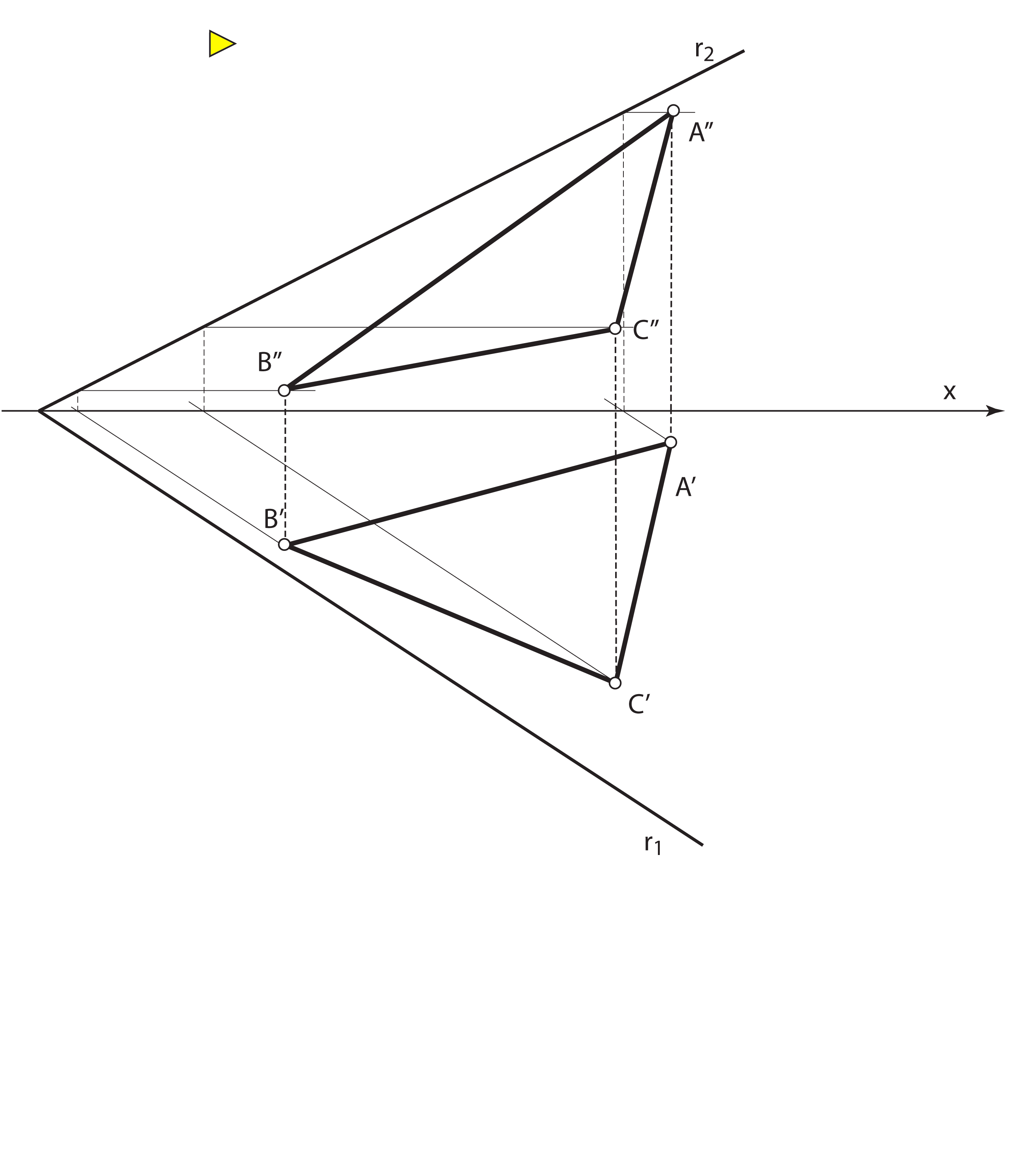
|
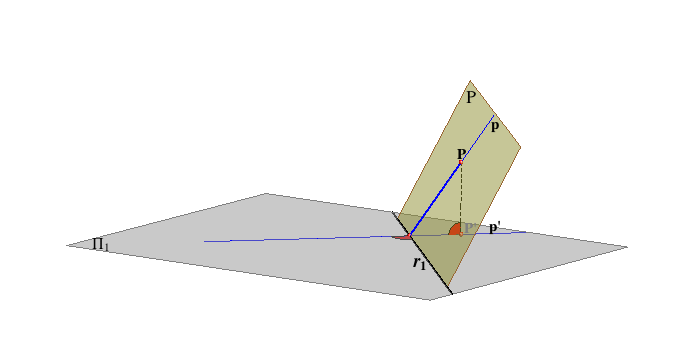
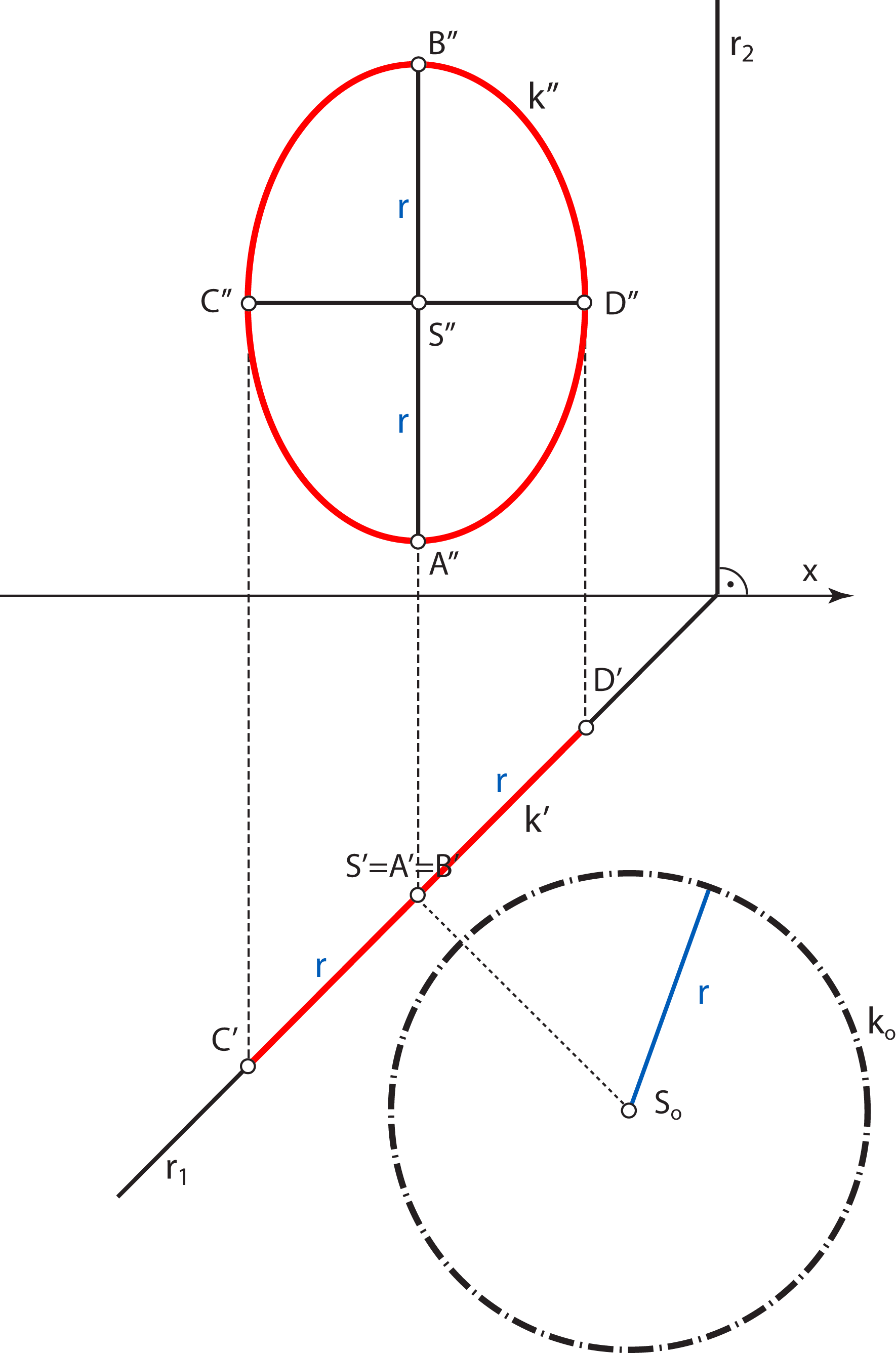
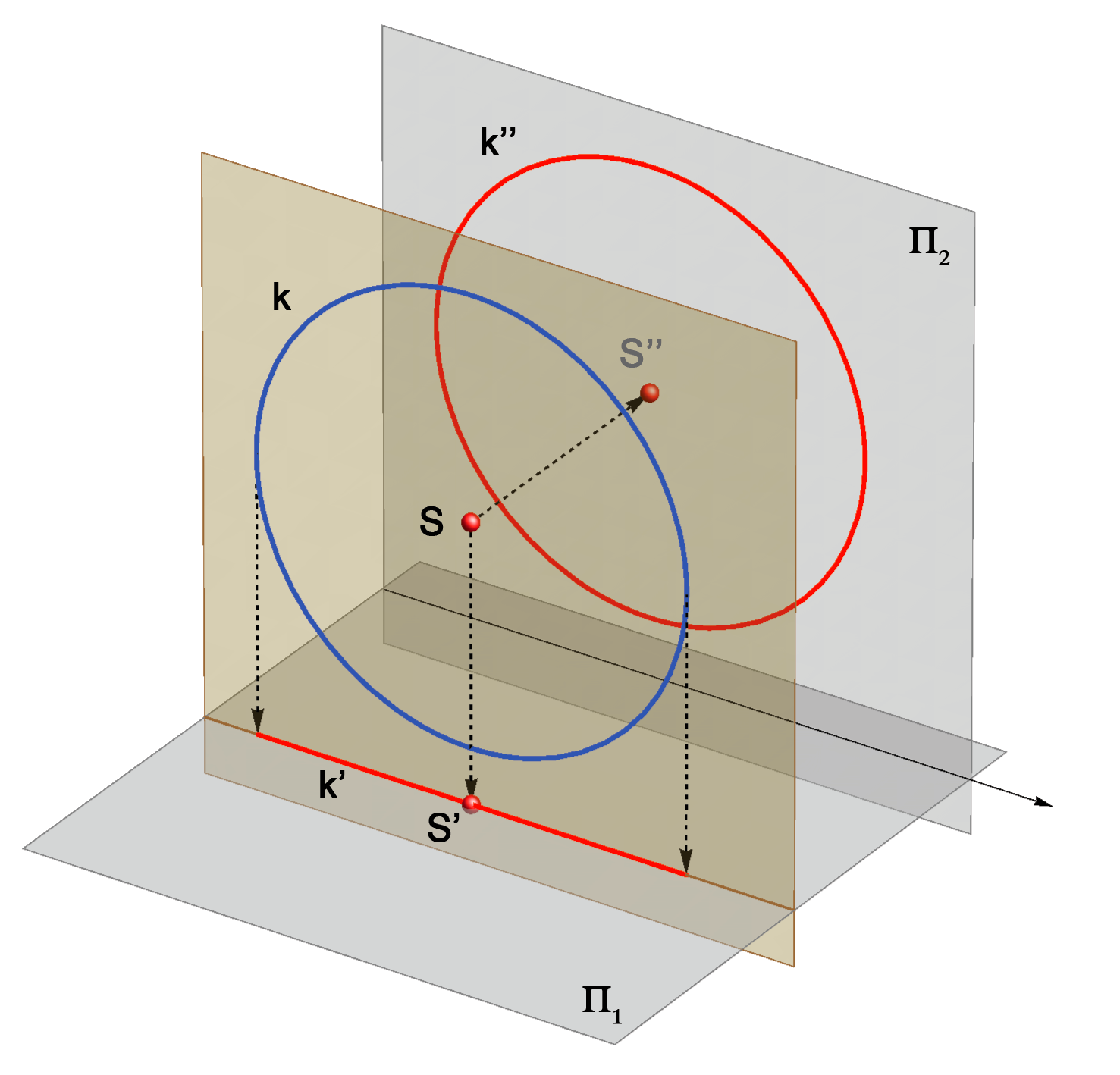
Notice the following: An axis of this transformation is the trace r1, rays are horizontal projections of the 1st steepest lines of the plane P. |
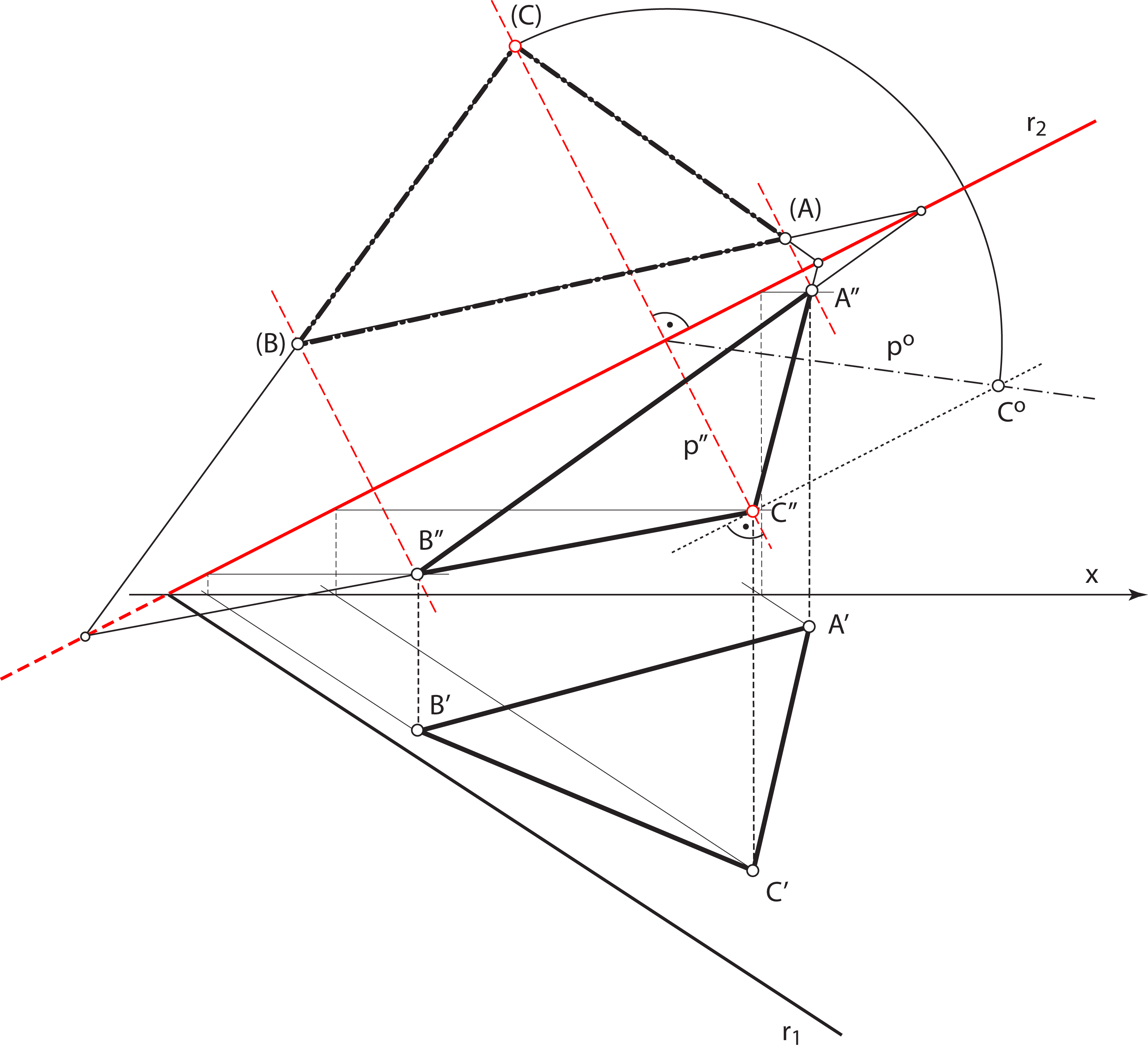
Click on the image to start the animation |
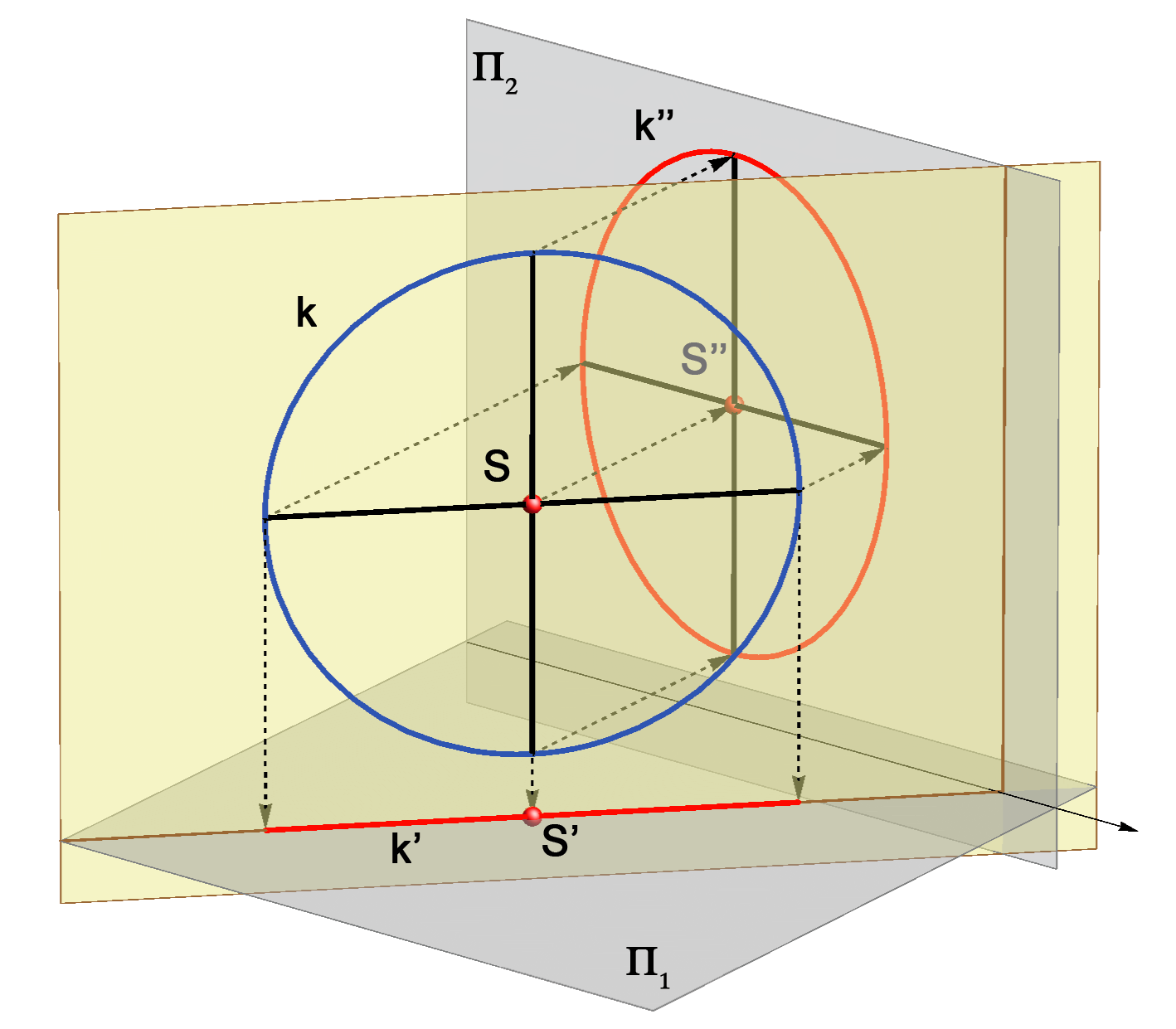
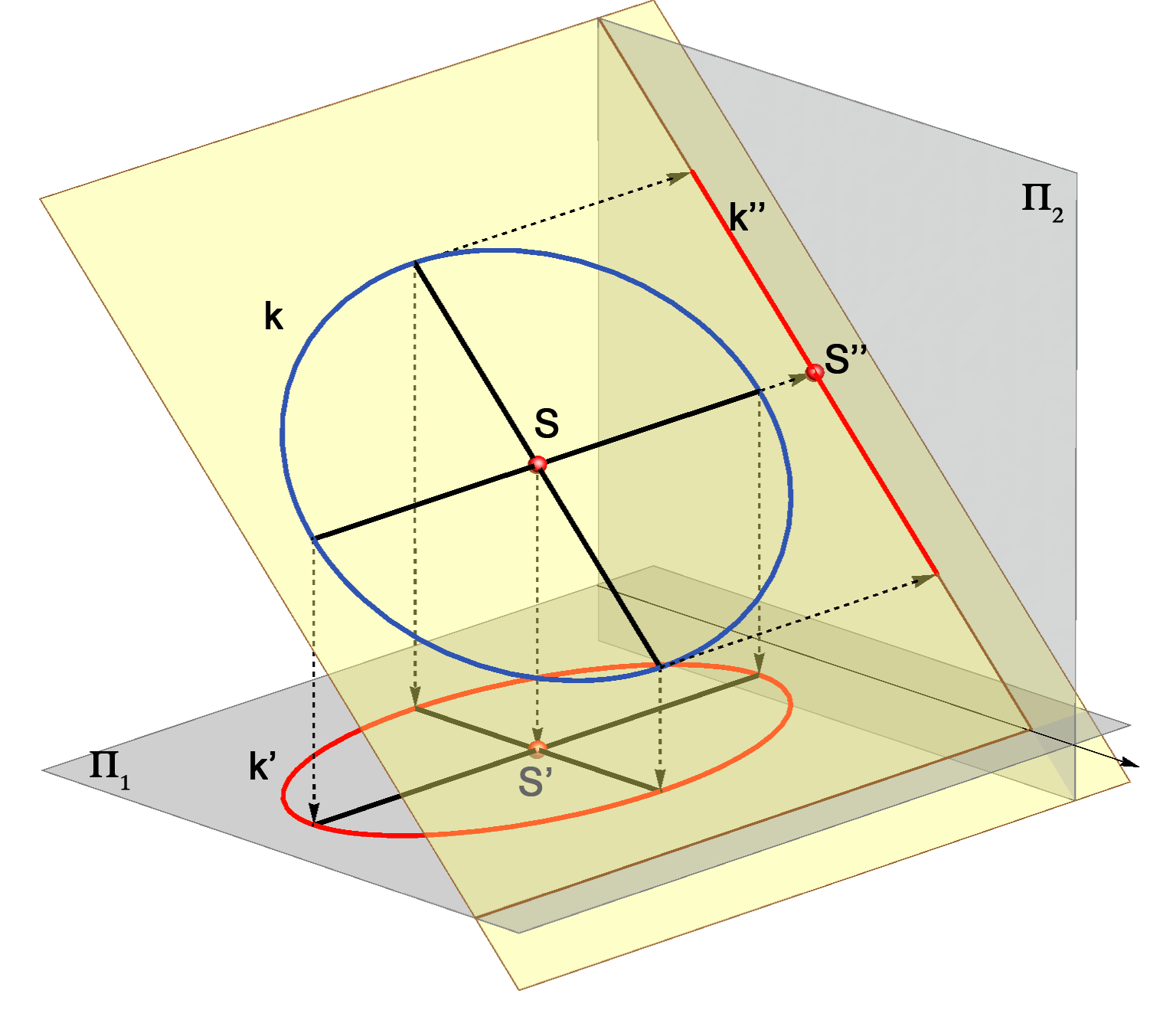
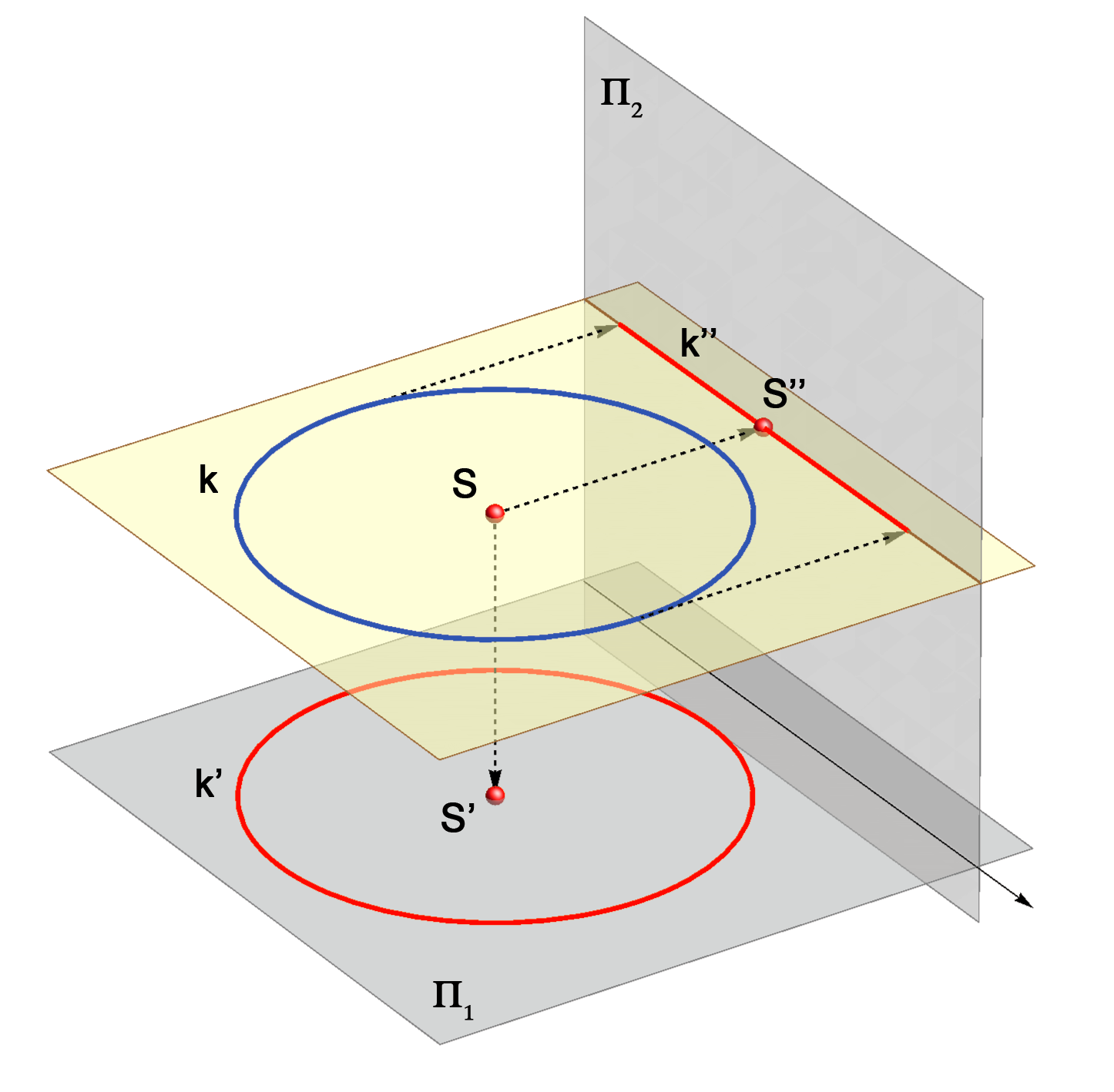
As the parallel lines and ratio of the line lengths are preserved in the
orthogonal projection, so the
following holds:
QUESTION: Which pair of orthogonal diameters of the circle k projects into the major and minor axis of the ellipse k'? |
|
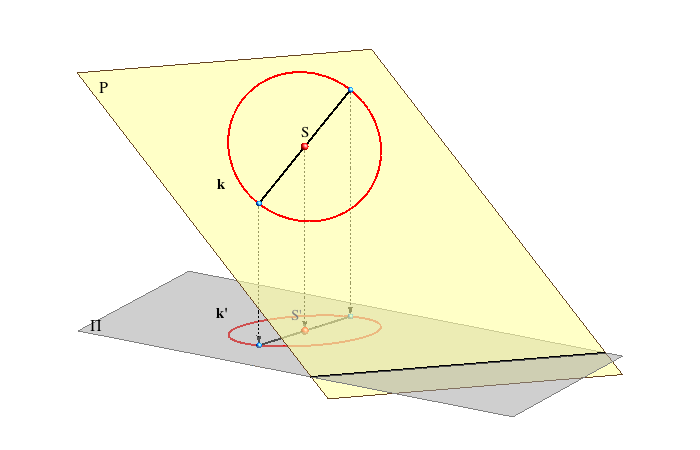
A length of the orthogonal projection of a line segment is smaller or the same (if
the line segment is parallel to the plane of projection) than the true length of
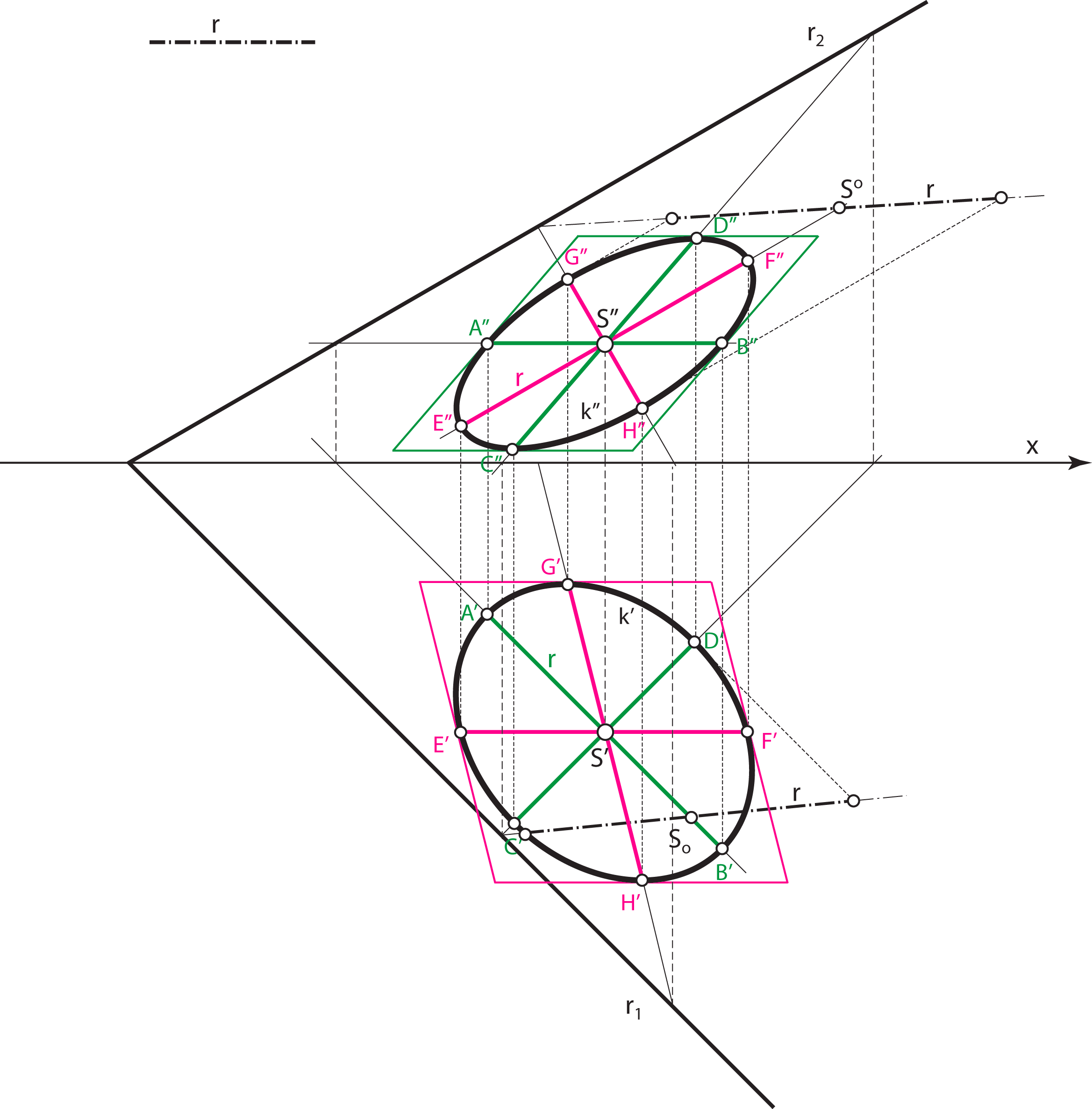
the line segment. Therefore, the diameter of the circle which is parallel to the plane of projection is projected into the longest diameter of the ellipse - its major axis. The minor axis is perpendicular to the major axis, so its projection lie on a line perpendicular to the projection of the major axis. This line has the largest angle of inclination to the plane of projection. Projections of the line segments on this line have the most reduced lengths. We conclude: |
|
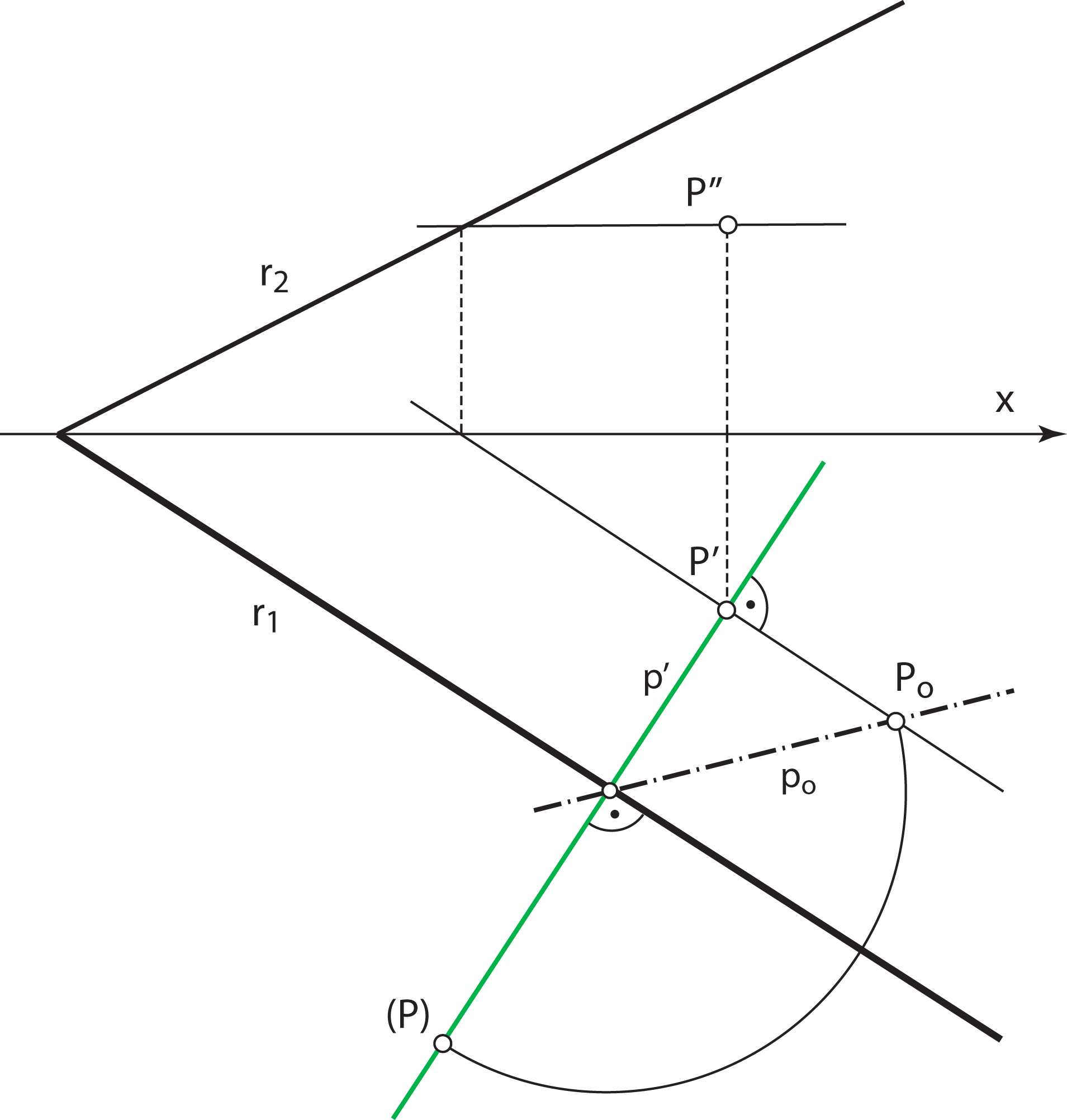
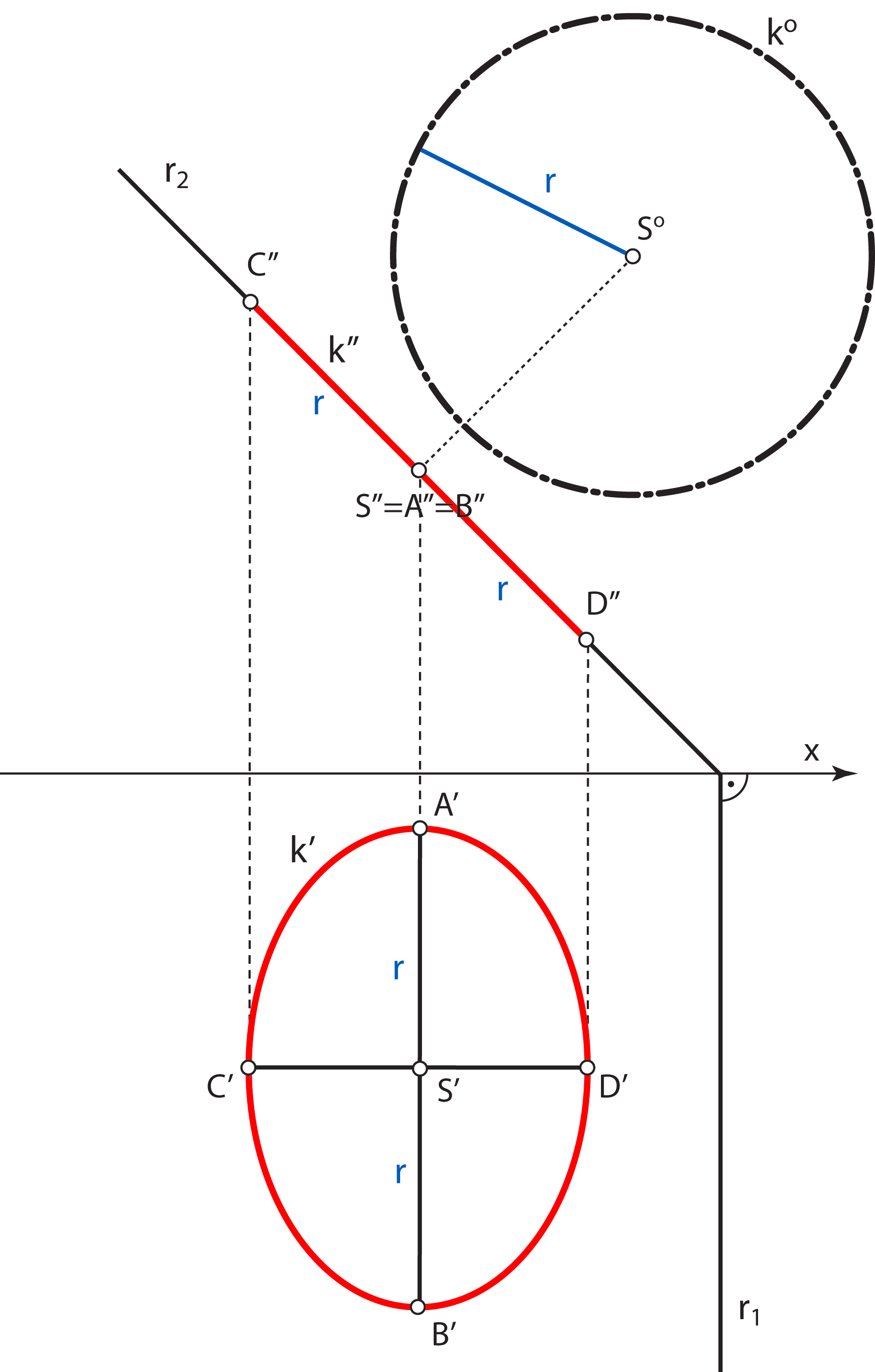
Construction : rotate this 2nd steepest line into the plane Π2 and lay the length 2r on the rotated line. The same holds for the construction of the major and minor axis of the horizontal projection of the circle. Construction : rotate this 1nd steepest line into the plane Π1 and lay the length 2r on the rotated line. |
|
|
|
|
|
|
|
|
Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja -3DGeomTeh - Developing project of the University of Zagreb