Algebraic Surfaces
An algebraic surface of order n is a set of points in
euclidean space whose coordinates satisfy certain algebraic equation \( F^n(x,y,z)=0\),
where \( F^n(x,y,z)\) is a polynomial of degree n.
An algebraic surface of the 1st order is a plane. It
is defined by a linear algebraic equation \( a\cdot x+b\cdot y+c\cdot z+d=0, \, a,b,c\in\mathbb R\).
A line in the space can be defined by two equations.
A line can be observed
as an
intersection of two planes, so in that case the coordinates of points of a line satisfy two
linear equations.
Three algebraic equations of degrees n, 1 and 1,
generally have n solutions, so in our class we will define the order of
the surface in the following manner:
An order of an algebraic surface equals the
number of intersections with any line in the
space that does not lie on this surface.
There are three types of such intersections: real and different two or more
intersections can coincide and conjugate imaginary points. For instance, if a line is
a tangent line at a point of a surface, then two intersection points will
coincide at the point of tangency of this line.
A set of points that belong to a surface and to a plane are called intersection
points of the surface and the plane.
Every plane intersection
of an algebraic surface is a plane algebraic curve.
From the definitions of orders of algebraic surfaces and algebraic curves we can deduce
the following:
The order of an algebraic surface equals the order of any plane intersection of that surface.
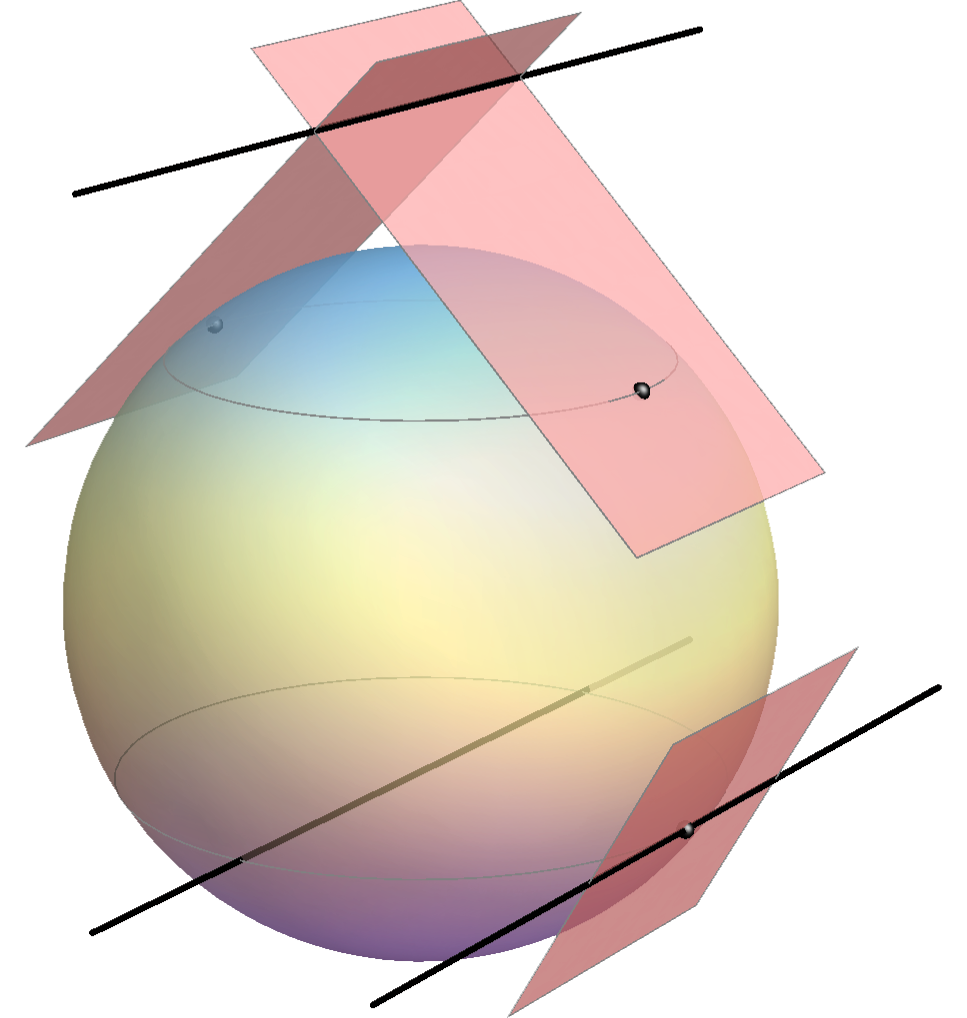
A dual notion of the order of a surface is the class of the surface. We define it in this way:
A class of an algebraic surface equals the number of its tangent planes that pass through any line in the space that doesn't lie on the surface.
If the order and the class of a surface equal n, we say that the surface is of
the nth
degree.
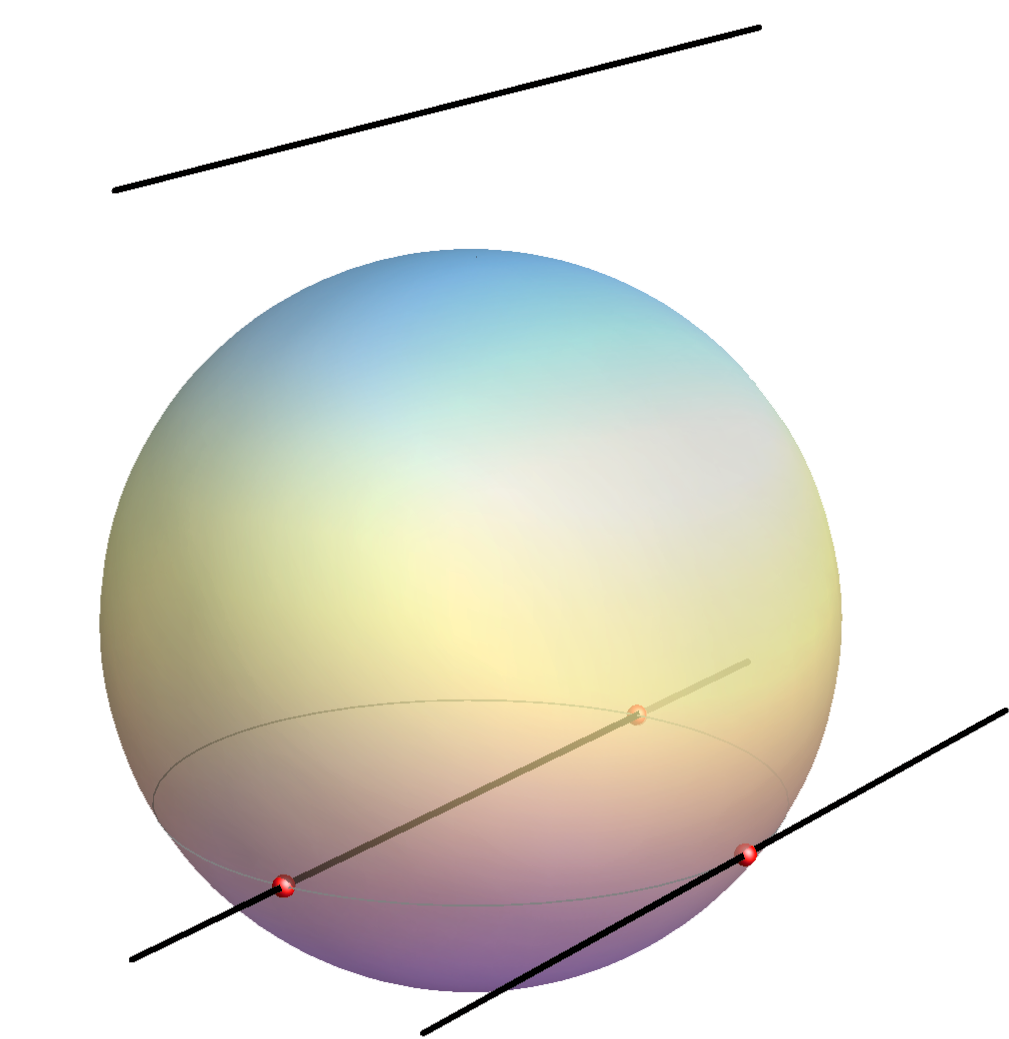
An example; the sphere is a surface of the 2nd degree.
Every line in the
space intersects the sphere in two points that can be real and different, they
can coincide (if the line is a tangent line) or imaginary.
Every line in the space lies in two tangent planes of the sphere. These
planes can be real and different (if the line intersects the sphere in two
imaginary points), they can coincide (if the line is tangent line) or can be
conjugate imaginary (if the line intersects the sphere in two real points).
Some algebraic surface of order greater than 2

\(z \left(x^2+y^2\right)-(3 x^2+y^2)=0\)
The Plücker conoid –
a ruled surface of the 3rd degree
|

\( x^2+y^2 z=0\)
The Whitney umbrella – a ruled surface
of the 3rd degree
|
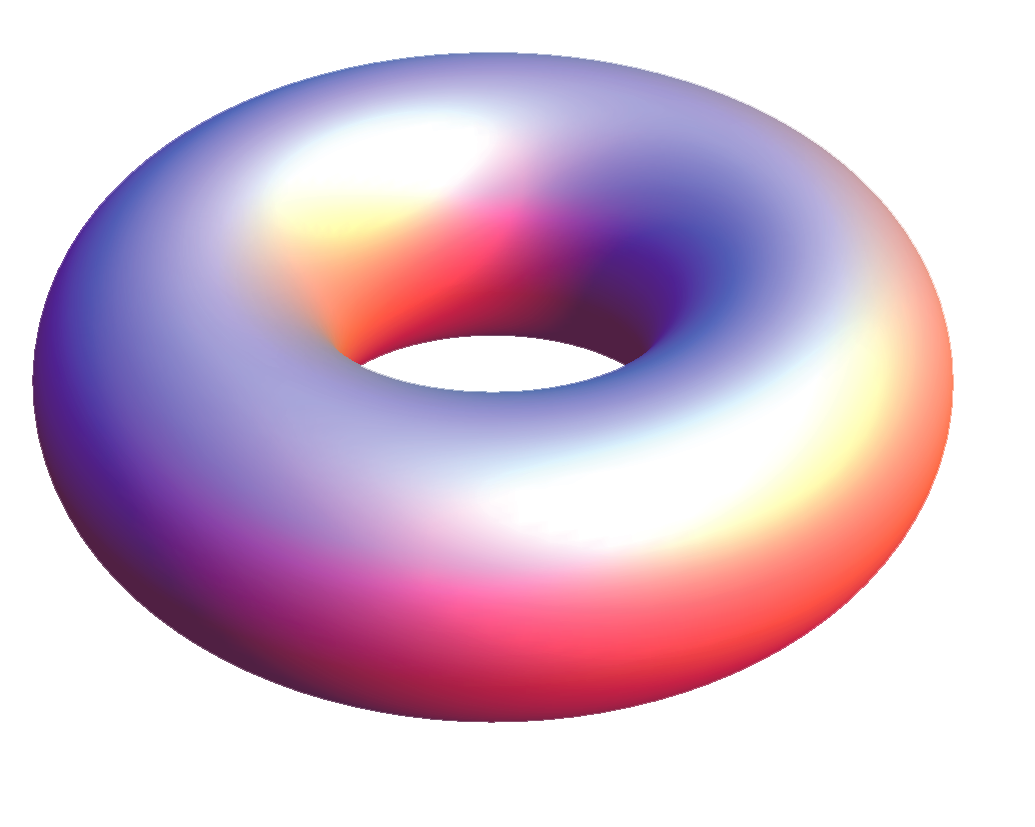
\(\left(x^2+y^2+z^2\right)^2-8 \left(5 x^2+5 y^2-3 z^2\right)+144=0 \)
The Torus –
a surface of the 4th order |
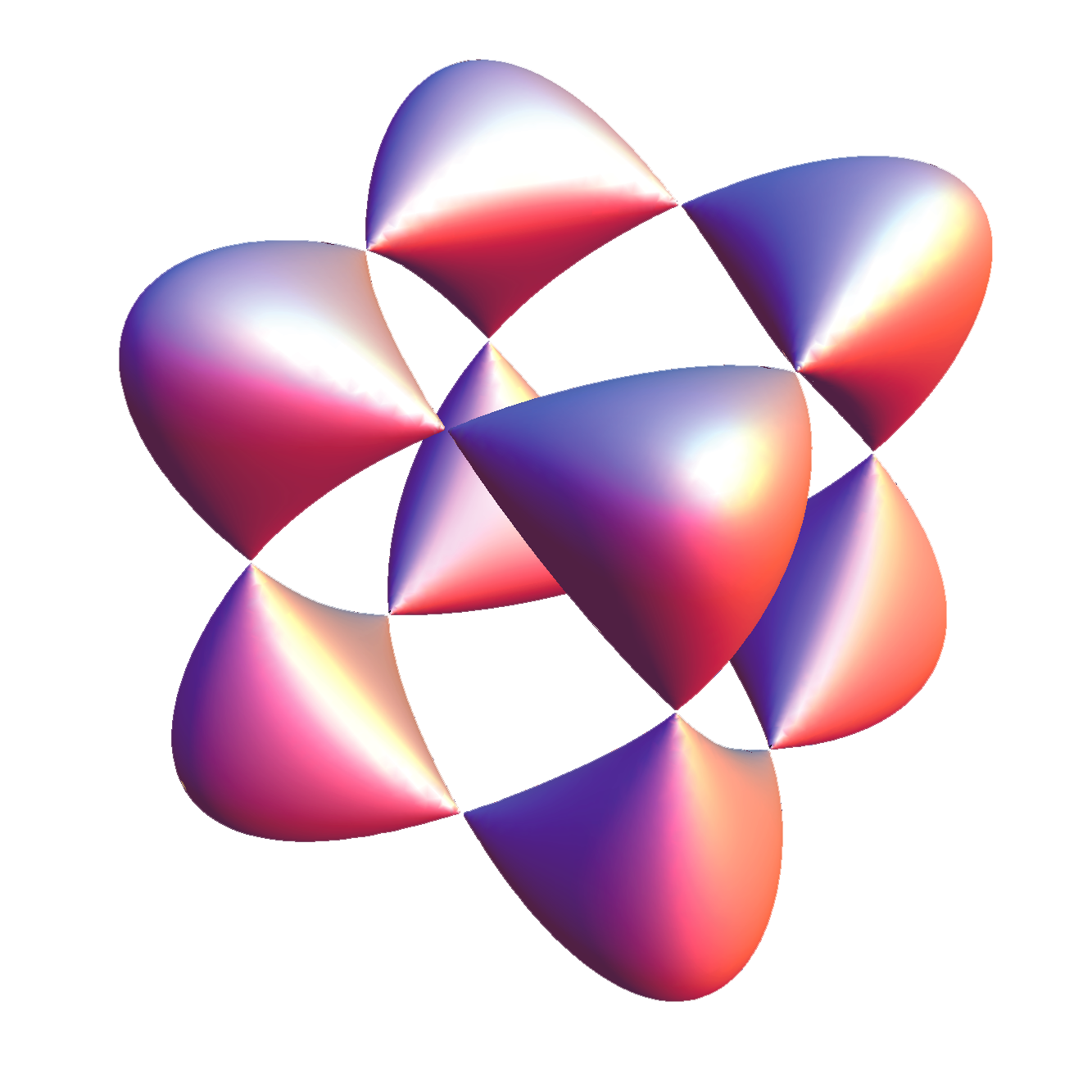 \( x^4+y^4+z^4-(x^2+y^2+z^2)+\frac{1}{2}=0\)
\( x^4+y^4+z^4-(x^2+y^2+z^2)+\frac{1}{2}=0\)
The Goursat surface –
a surface of the 4th order
|
Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb


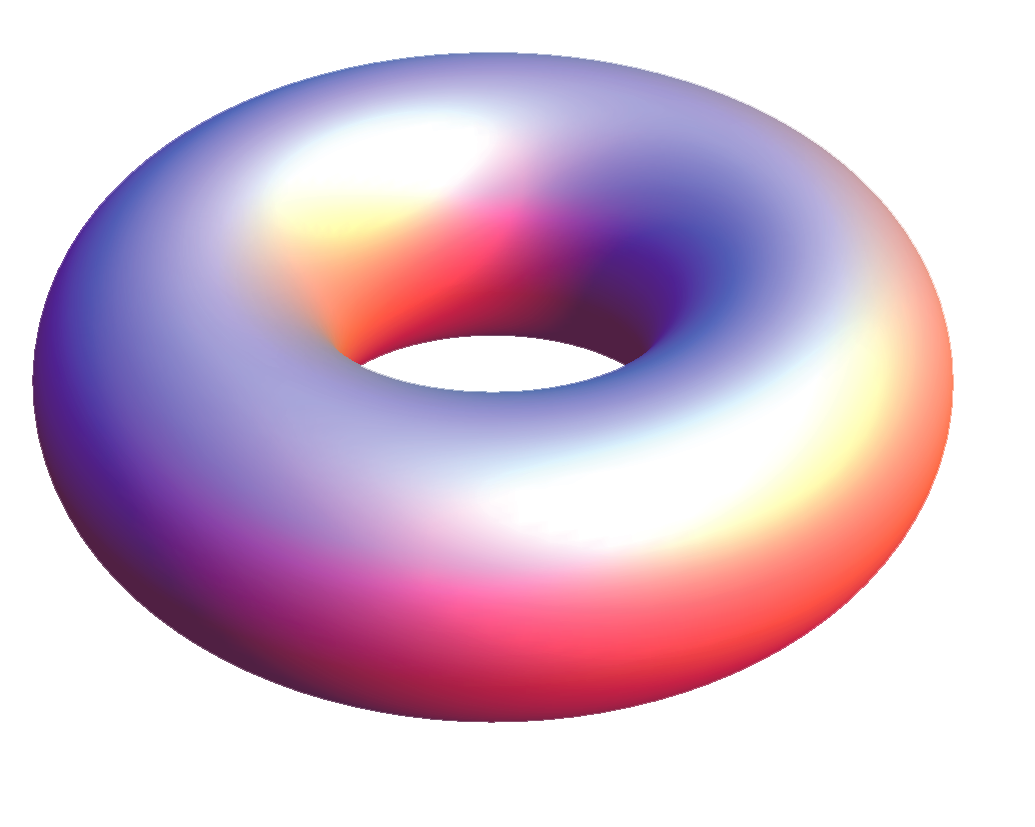
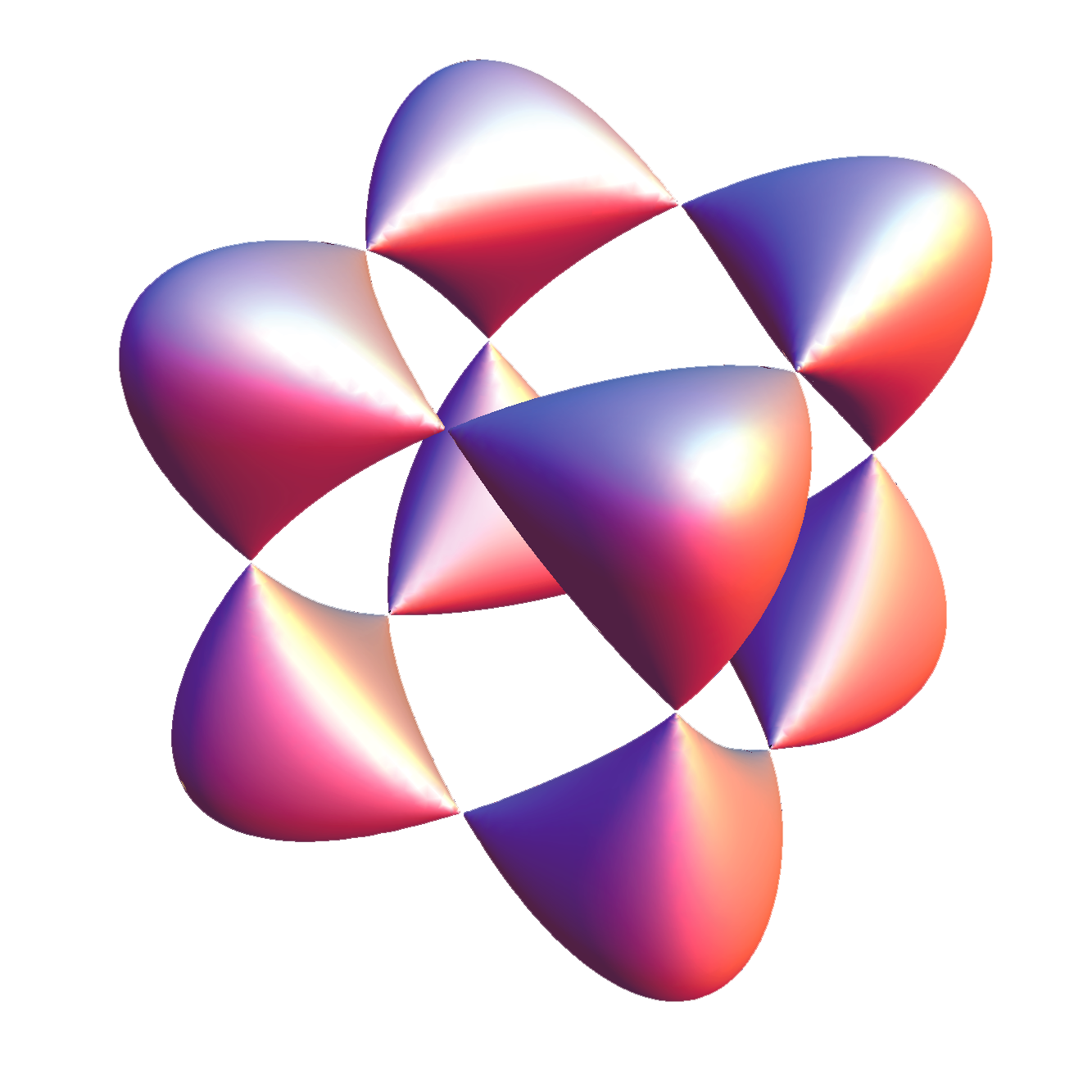 \( x^4+y^4+z^4-(x^2+y^2+z^2)+\frac{1}{2}=0\)
\( x^4+y^4+z^4-(x^2+y^2+z^2)+\frac{1}{2}=0\)