Cones and Cylinders - (Conical and cylindrical surfaces)*

* A cone and a cylinder are bounded geometrical objects - the cone is bounded by a plane (a base of the cone) and its lateral surface - a conical surface, the cylinder is bounded by two planes (two bases) and a cylindrical surface. We will not distinguish between a cone and a conical surface and a cylinder and a cylindrical surfaces, if not stated otherwise. We consider them as infinite surfaces (not bounded).

  • A cone is a locus of lines connecting points on a plane or a space curve with one point that doesn't lie in the plane of the curve.
    The point is called the vertex (or the apex) of the cone and the connecting lines are called the generatrices of the cone.

  • A cylinder is a locus of lines connecting points on a plane or a space curve with one point at infinity that doesn't lie in the plane of the curve(in the case of plane curves).
    These connecting lines are called the generatrices of the cylinder and they are parallel to each other. The point at infinity on a generatrix (all generatrices have the same point at infinity) is called the vertex of the cylinder.

  • Cones and cylinders are ruled surfaces.

    right-click \( \rightarrow \) PLAY
    right-click  \( \rightarrow \) PLAY


  • If a curve k is the nth order algebraic curve and the vertex is not on this curve, the cone or the cylinder determined by this curve is an algebraic surface of order n.

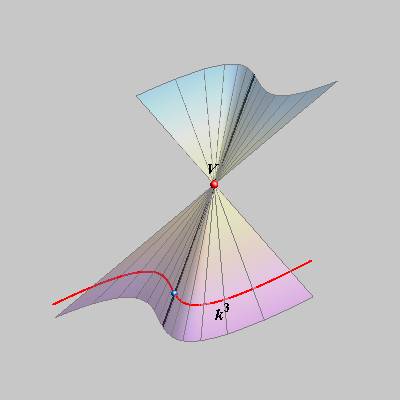
    the 3rd degree cone.
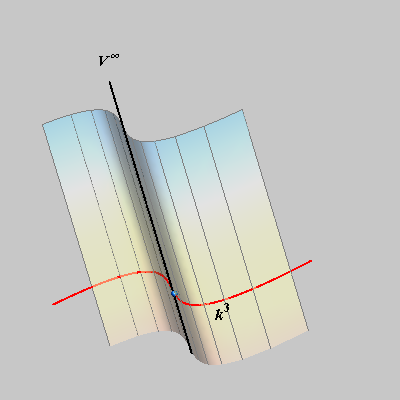
    the 3rd degree cylinder.



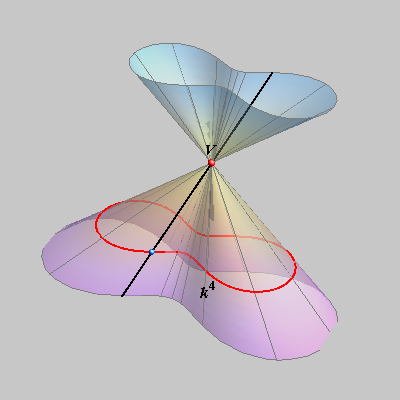
    the 4th degree cone.
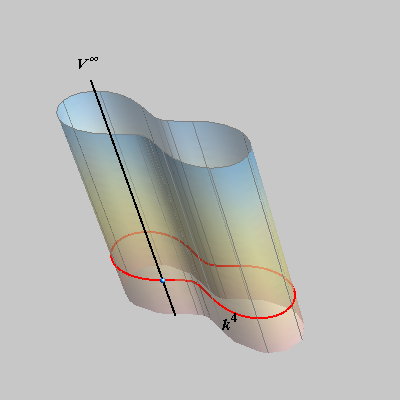
    the 4th degree cylinder.


    We will work only with cones and cylinders of the 2nd degree.


    Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb