The 2nd degree cylindres

  • The 2nd degree cylinders are algebraic ruled surfaces whose rulings are lines connecting points of a non-degenerated conic and one point at infinity (a vertex)  \(\mathbf{V}^\infty\).
    All rulings (generatrices) of a cylinder are parallel.

    Plane intersections of the 2nd degree cylinders

    Similar to the plane intersections of the 2nd degree cones, their intersection is a degenerated conic  if the plane contains the vertex of the cylinder. If the plane doesn't contain the vertex, their intersection is a proper conic.

    1. A plane contains the vertex of the cylinder

    If the plane (different from the plane at infinity) pass through the vertex of the cylinder (the plane is then parallel to all generatrices of the cylinder) , the intersection is degenerated conic - two generatrices that can be:

  • a pair of real parallel lines,

  • one real double line,

  • a pair of conjugate imaginary lines that intersect in a real point.


    two real parallel generatrices
    two coinciding generatrices - tangent plane
    two imaginary parallel generatrices

    desni klik za pokretanje animacije



    The plane at infinity also intersects the cylinder in two generatrices. There are three types of cylinders with respect to this intersection:

  • hyperbolic (two real generatrices that are lines at infinity)

  • parabolic (one double real generatrix that is a line at infinity)

  • elliptic (a pair of conjugate imaginary generatrices at infinity).


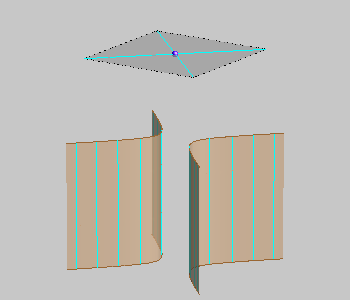
    hyperbolic cylinder
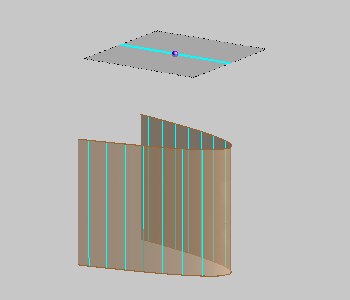
    parabolic cylinder

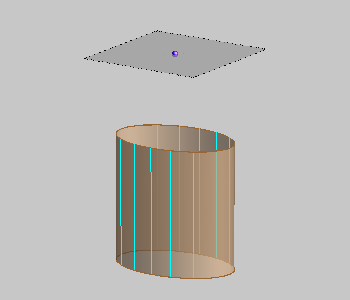
    elliptic cylinder


    2. A plane doesn't contain the vertex of the cylinder

    If a plane is not parallel to the generatrices of a cylinder, its intersection with the 2nd degree cylinder is a proper conic.

    The type of this conic (hyperbola, parabola or ellipse) depends on the type of the cylinder.

    The plane that is not parallel to the generatrices of a cylinder intersects the cylinder in:

  • a hyperbola, if the cylinder is hyperbolic,

  • a parabola, if the cylinder is parabolic,

  • an ellipse, if the cylinder is elliptic.


    A plane intersection of a hyperbolic cylinder is HYPERBOLA.
    A plane intersection of a parabolic cylinder is PARABOLA.
    A plane intersection of an elliptic cylinder is ELLIPSE.

    right-click to start the animation



    A tangent plane of the 2nd order cylinder

    Tangent planes of a cylinder pass through its vertex (point at infinity) and they are parallel to generatrices of the cylinder.

  • The vertex of a cylinder is its singular point.

    All other points of a cylinder are regular - they have an unique tangent plane.

  • Tangent plane of a cylinder intersects the cylinder along one line (a generatrix).

  • All points of a generatrix of a cylinder have the same tangent plane.

  • A tangent plane of a cylinder at a regular point is determined by the generatrix passing through that point and any tangent line of the cylinder at that point.
    		•

    right-click to start the animation
  • There are two tangent planes to the cones through every point in the space that does not belong to the cylinder. 

    These planes can be real or imaginary.

    The construction of these planes is given in the animation on the right side.








    • Click on the image to start the animation..


  • A tangent at a point of the intersection curve of a cylinder and a plane is the intersection line of that plane and the tangent plane of the cylinder at that point.

    A cylinder of revolution

    We will do constructive exercise dealing only with the cones of revolution - circular cylinders.
    A circular cone is obtained by rotating one line about another parallel line (axis of rotation).
    Every plane perpendicular to the axis intersects the circular cylinder at a circle.

    A cylinder will be given by one circle intersection called a  base of the cylinder and its height.
    Point of a generatrix that lies on the base is called  a foot of the generatrix.

    Constructive assignments:

  • An intersection of a line and a cylinder.
  • A tangent plane at a point on a cylinder.
  • A tangent plane through a point not lying on a cylinder.


    Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb