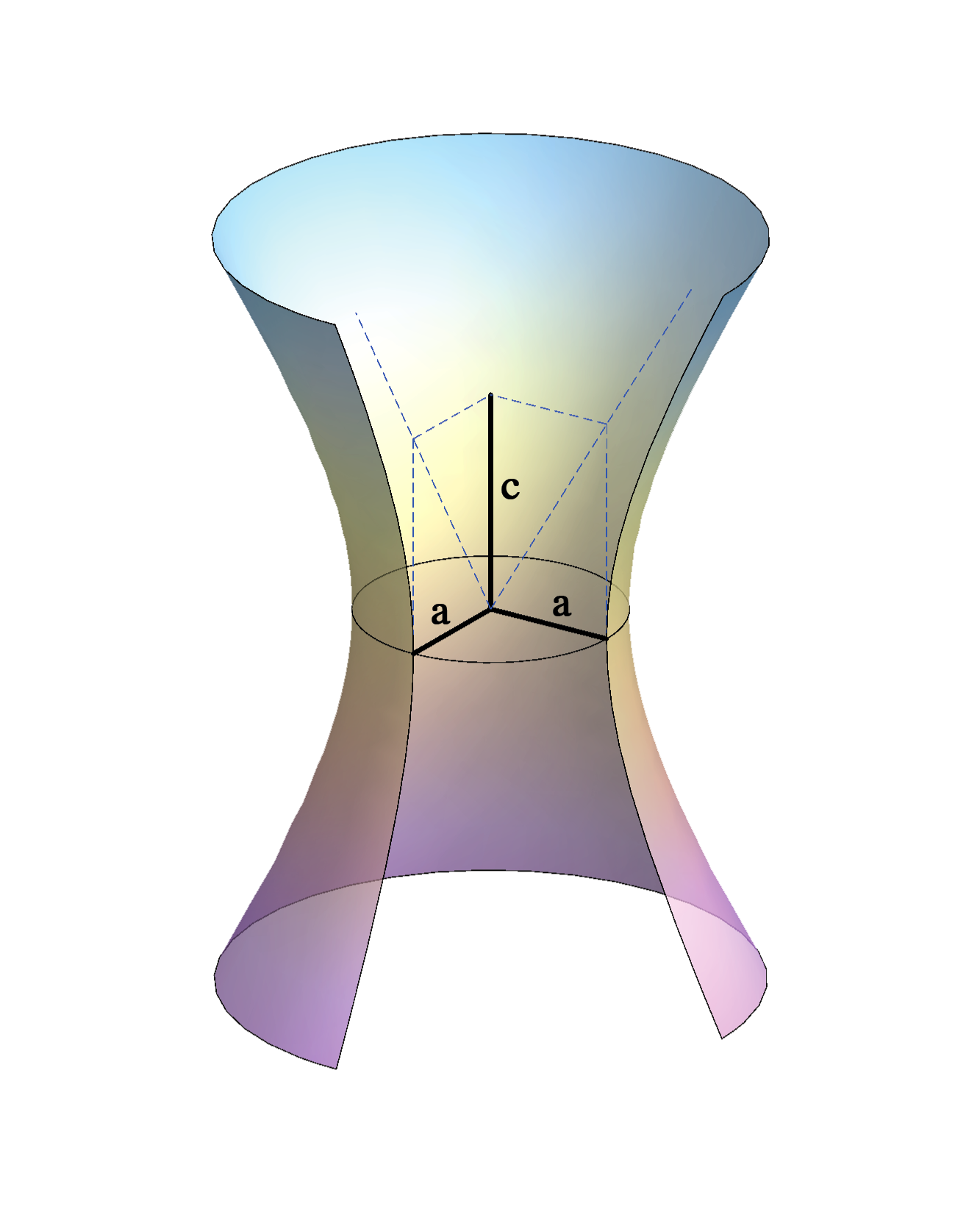
Circular hyperboloid of one sheet
\(\frac{x^2}{a^2}+\frac{y^2}{a^2}-\frac{z^2}{c^2}=1\)
Obtained by rotating a hyperbola around its conjugate (minor) axis,
or
by rotating one
line around another line when these lines are skew.
right-click \( \rightarrow \) PLAY
This hyperboloid is doubly ruled surface - has two systems of ruling.
Through each point passes one ruling from each system.
All rulings in one system are skew lines.
Each ruling from one system intersects all rulings from the other system.

On the smallest circle of the hyperboloid lie the vertices of cross-section hyperbolas(intersections with planes that contain the axis).
Smallest circle contains those points of the rulings that are closest to the axis.
Orthogonal projections of the rulings to the plane of the smallest circle (or a plane parallel to that plane) are tangents of the smallest circle.
Tangent planes in the points on the smallest circle are parallel to the axis.
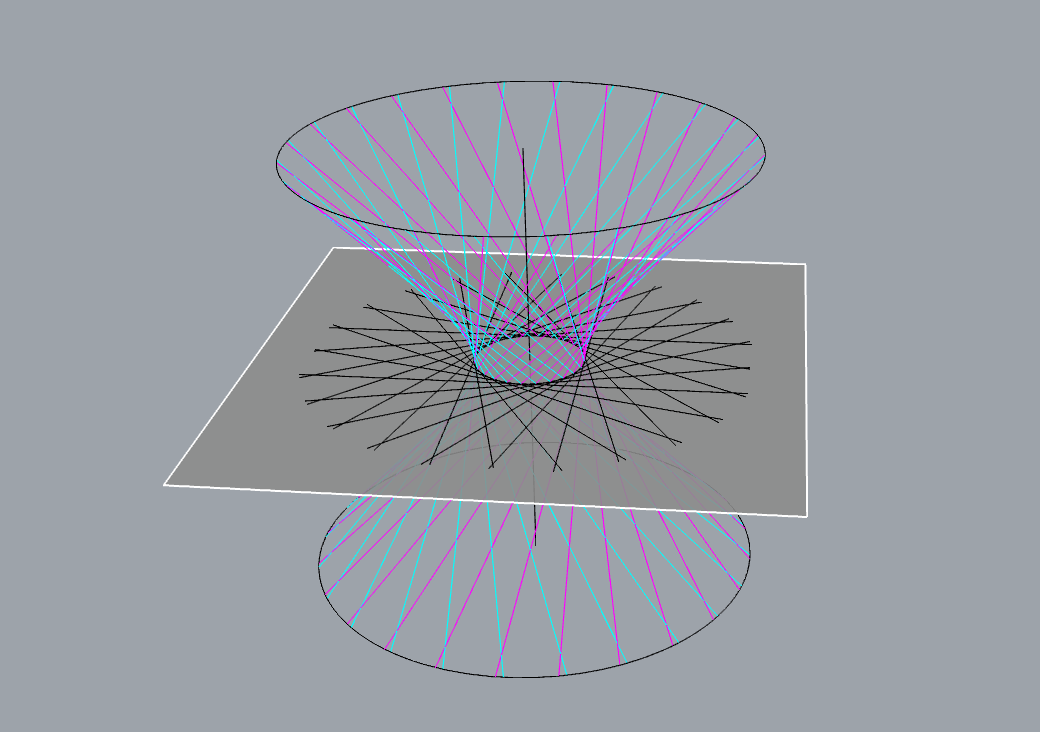
Asymptotic cone of one-sheeted hyperboloid
right-click \( \rightarrow \) PLAY
Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb