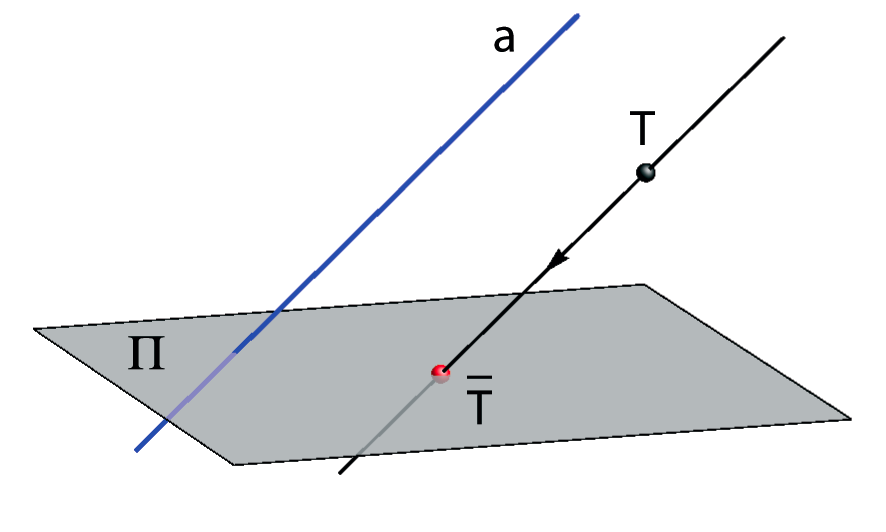
- Lines parallel to line a are called rays of projection and the plane Π is called the projection plane.
|
- Let a plane Π and a line a, which are not parallel, be given in space.
- Lines parallel to line a are called rays of projection and the plane Π is called the projection plane. |

|
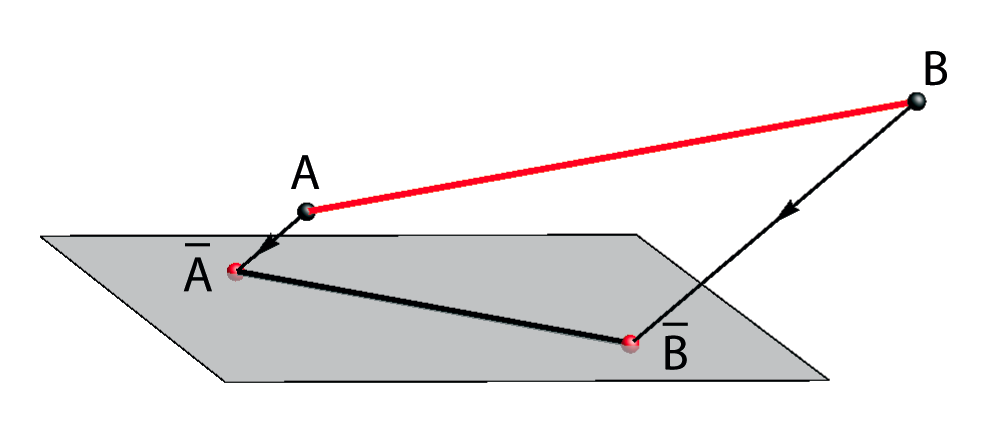
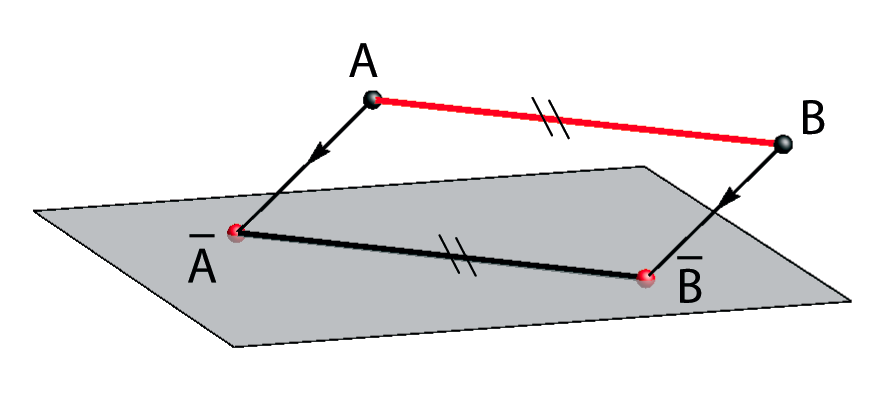
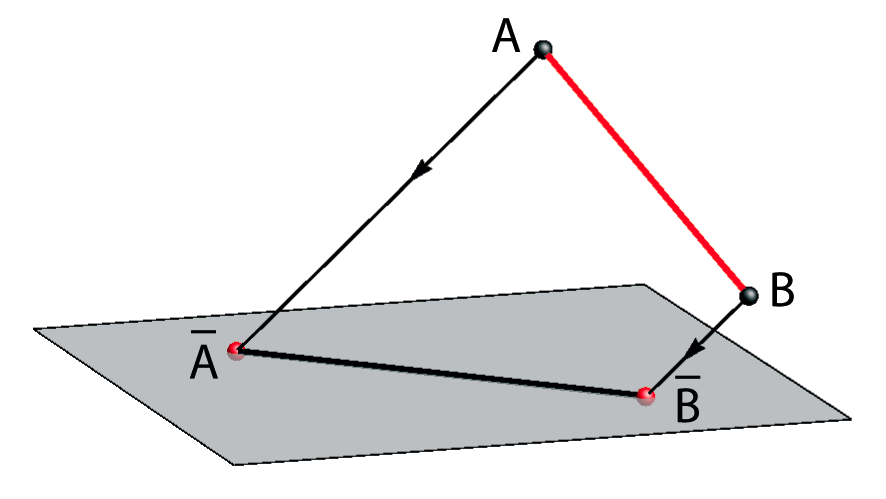
Some properties of the oblique parallel projection |
|
|
|
| d(A,B) < d(A,B) | d(A,B) = d(A,B) | d(A,B) > d(A,B) |
|
Plane figure determined by three line segments O A, O B and O C is called the plane three-frame and is denoted by O(A,B,C). (See the lower figure.) 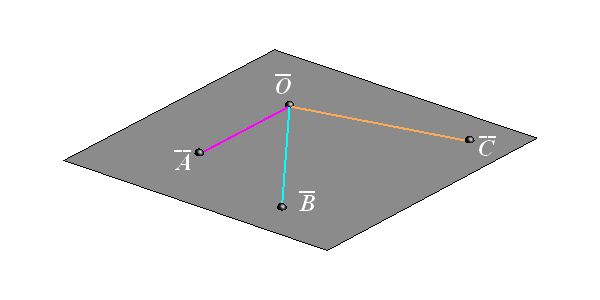
|
|
Let O(A,B,C) be the orthonormal three-frame in space for which no line segment is parallel to the ray of projection. Then the following is valid:
A plane three-frame O(A,B,C) obtained by this way is also called Pohlke's three-frame. for starting the animation: right click -> PLAY |
|
The proof of this theorem is not simple and it will not be shown here. |

|
|
|
|
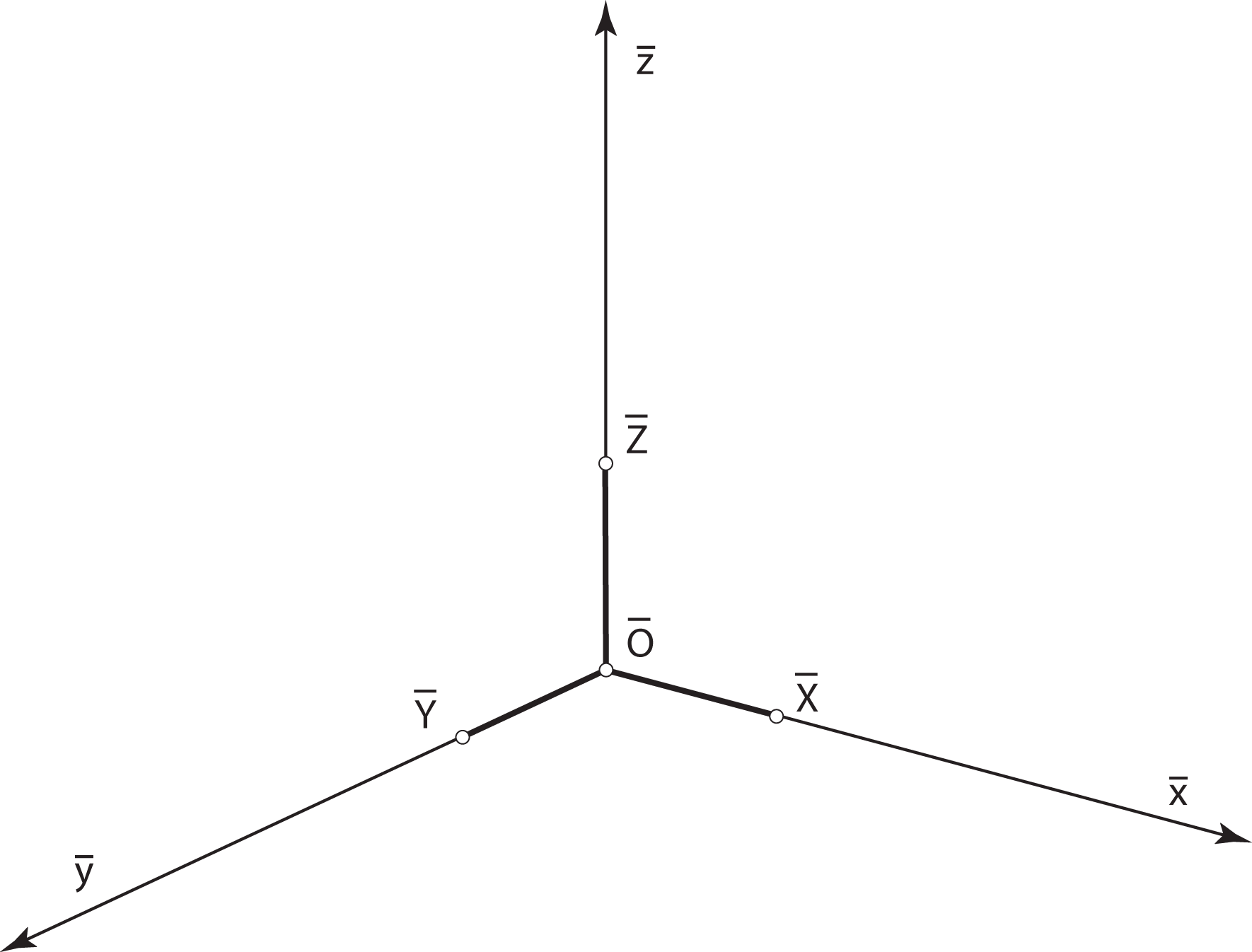
Axonometric image of a three-frame. The y-axis is usually put in the vertical position. |
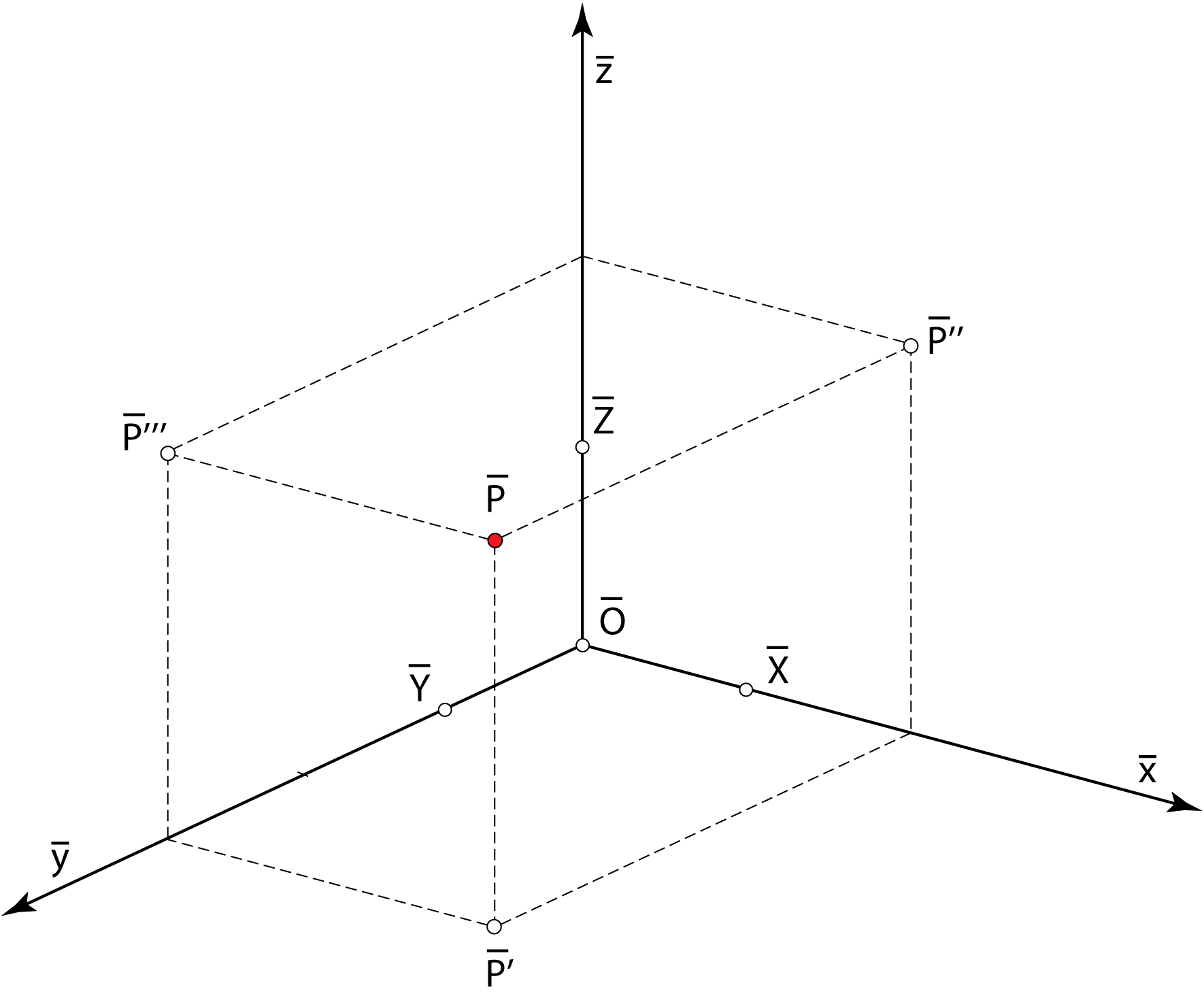
Axonometric image of the point P(2,3,2). |
|
|
Created by Sonja Gorjanc - 3DGeomTeh - Developing project of the University of Zagreb
Translated by Helena Halas and Iva Kodrnja