Elevated Projection

In Monge's projection the position of a point in space was uniquely determined by two of its orthogonal projection, usually with its horizontal and vertical projection.
It is also common to have a situation where the use of two projection is not possible or is inconvenient.
In these cases, we observe the orthogonal projection to only one plane and add an additional data as a number, which is the distance of a point and plane
of projection i.e. elevation of a point.
This projection is called elevated projection or projection with elevation.

The horizontal plane is usually chosen for the projection plane. All the points in this plane have elevation 0.

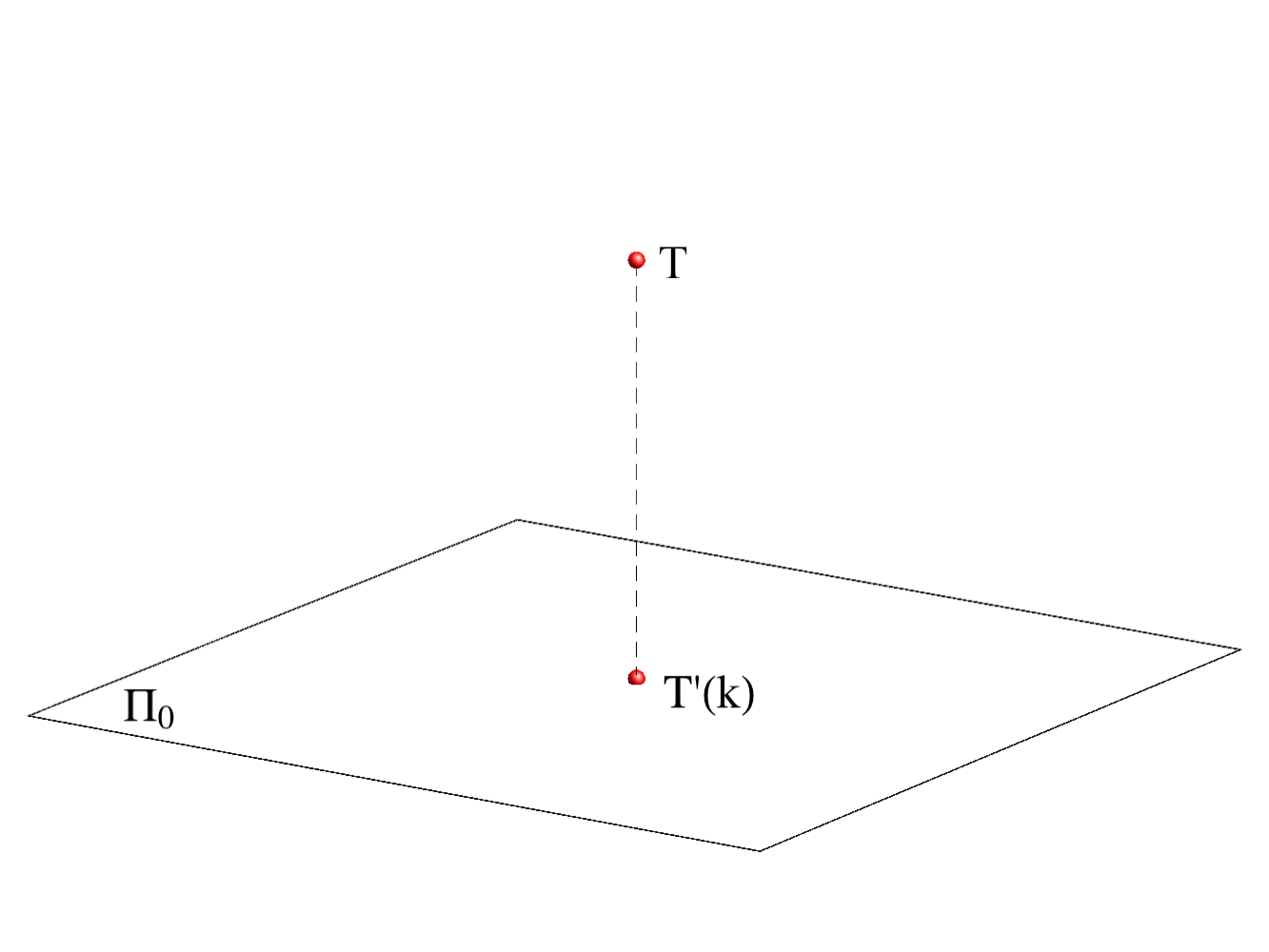
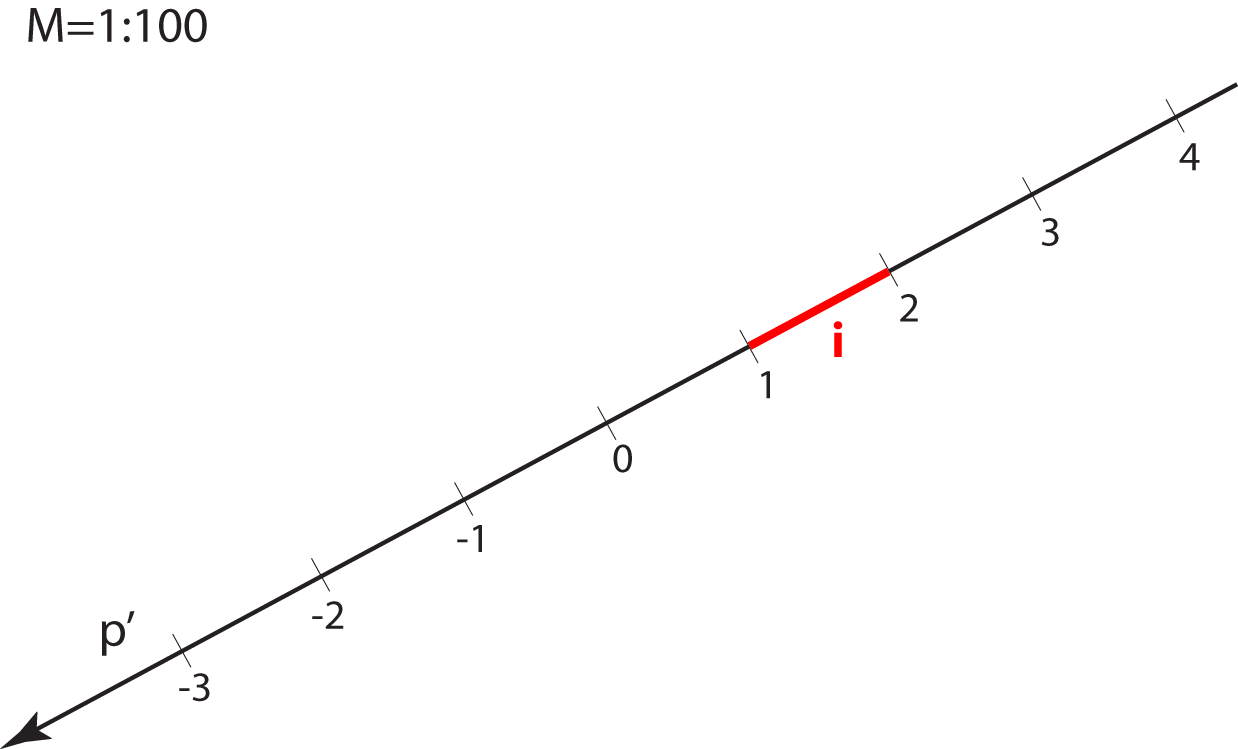
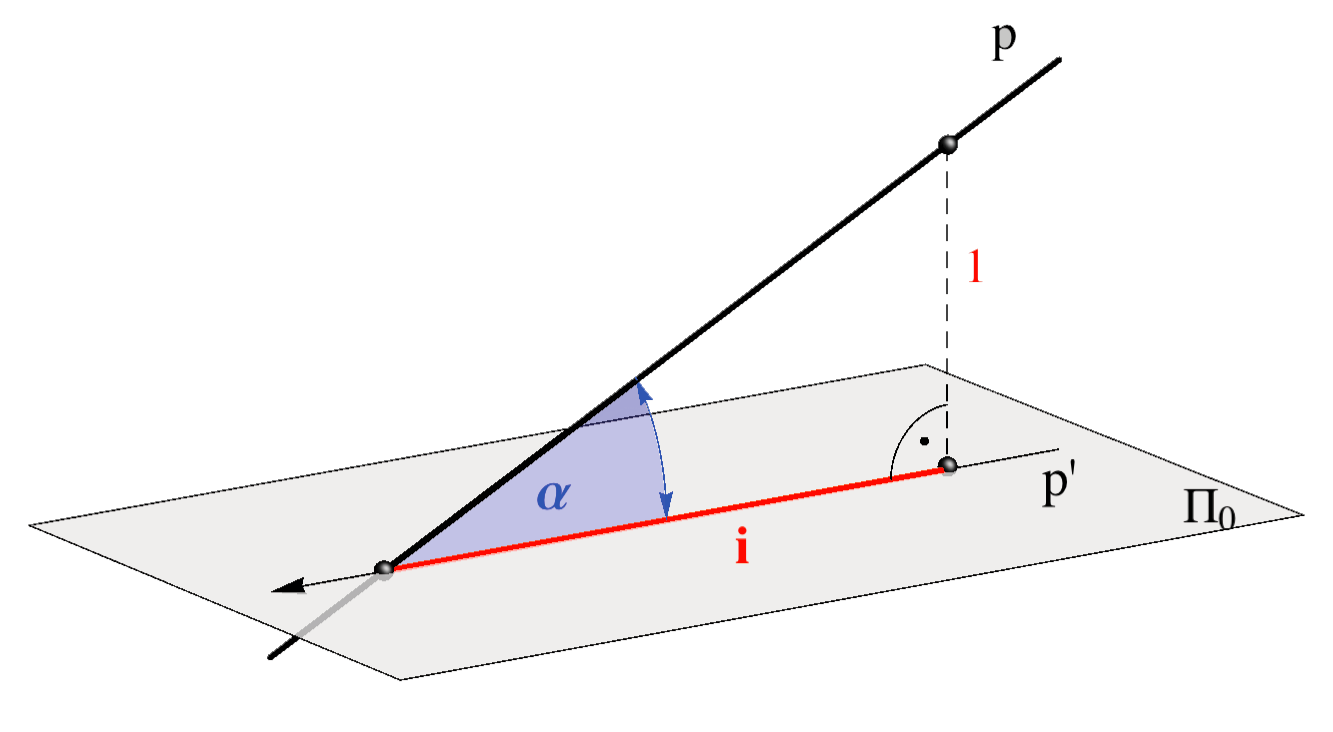
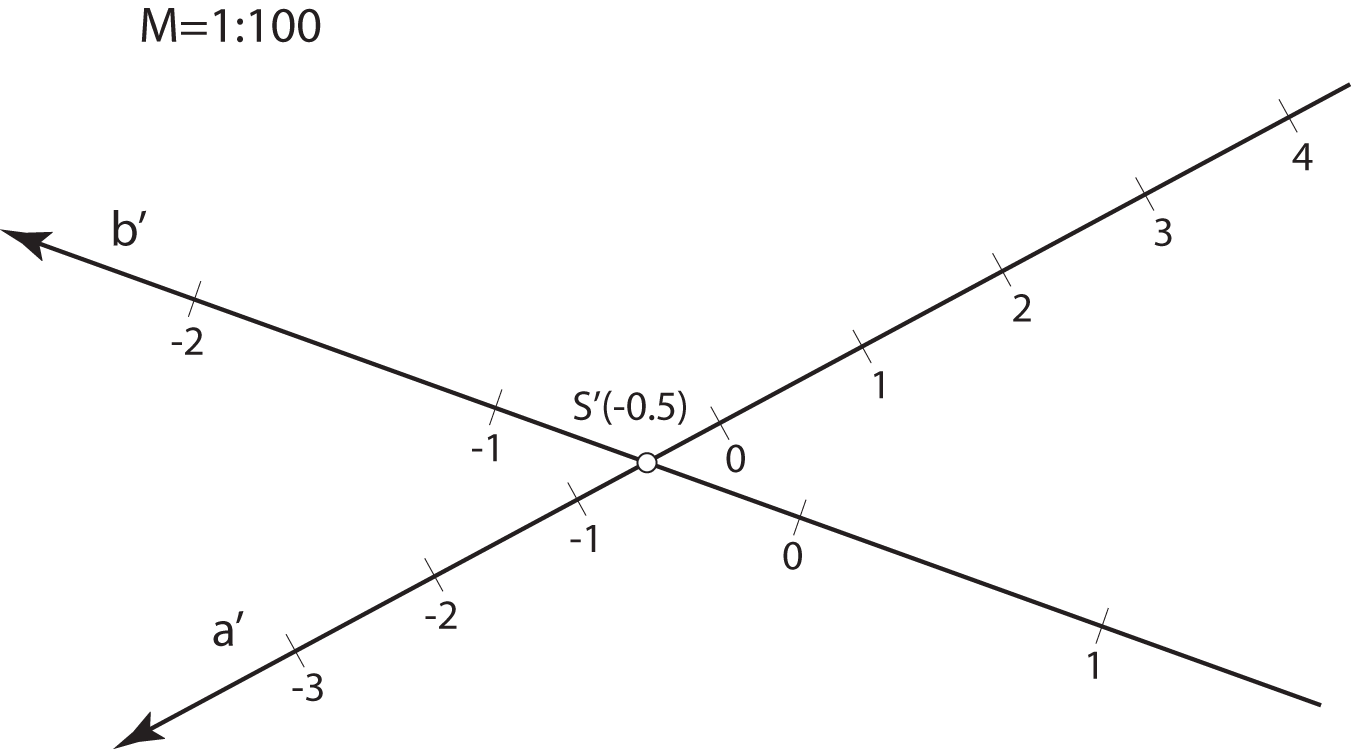
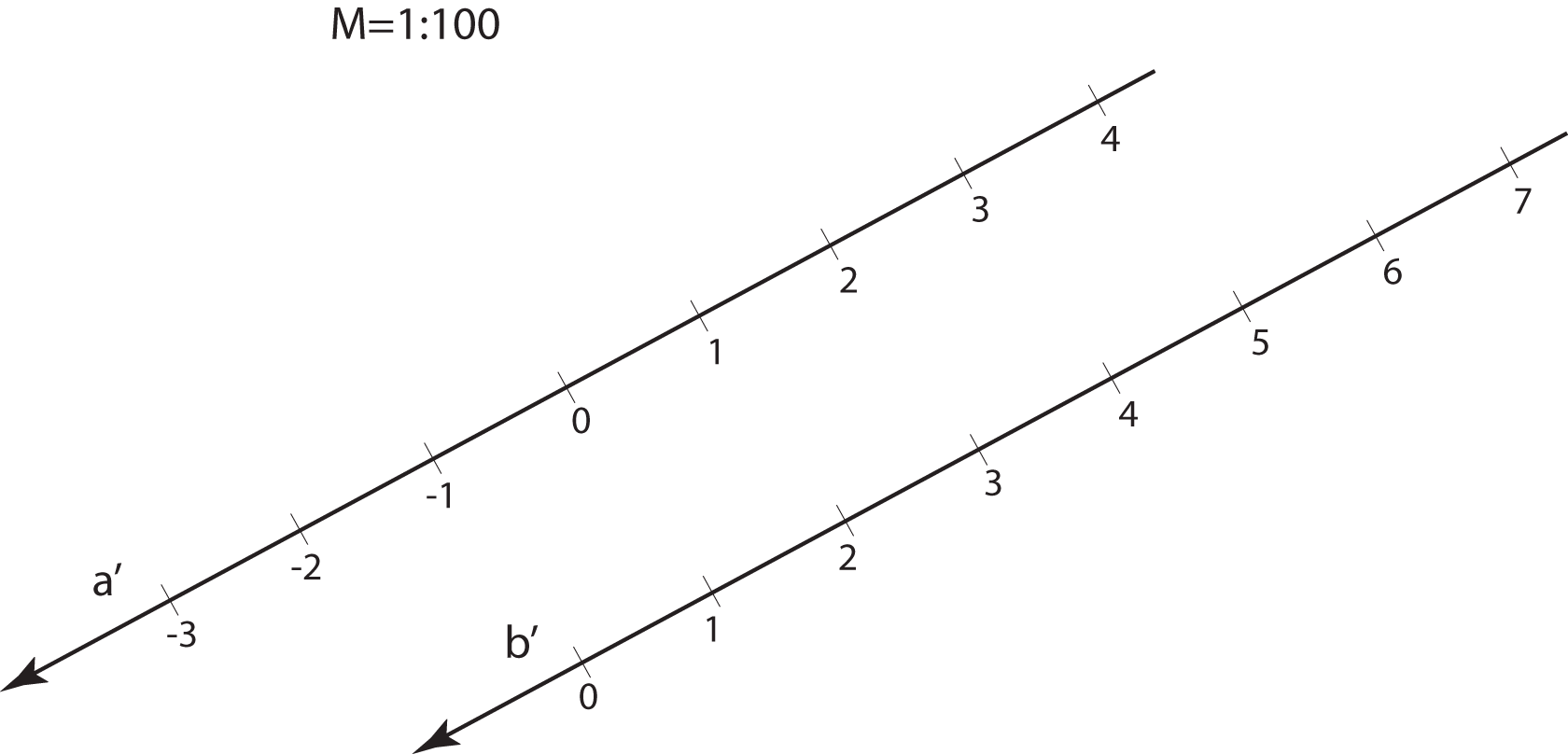
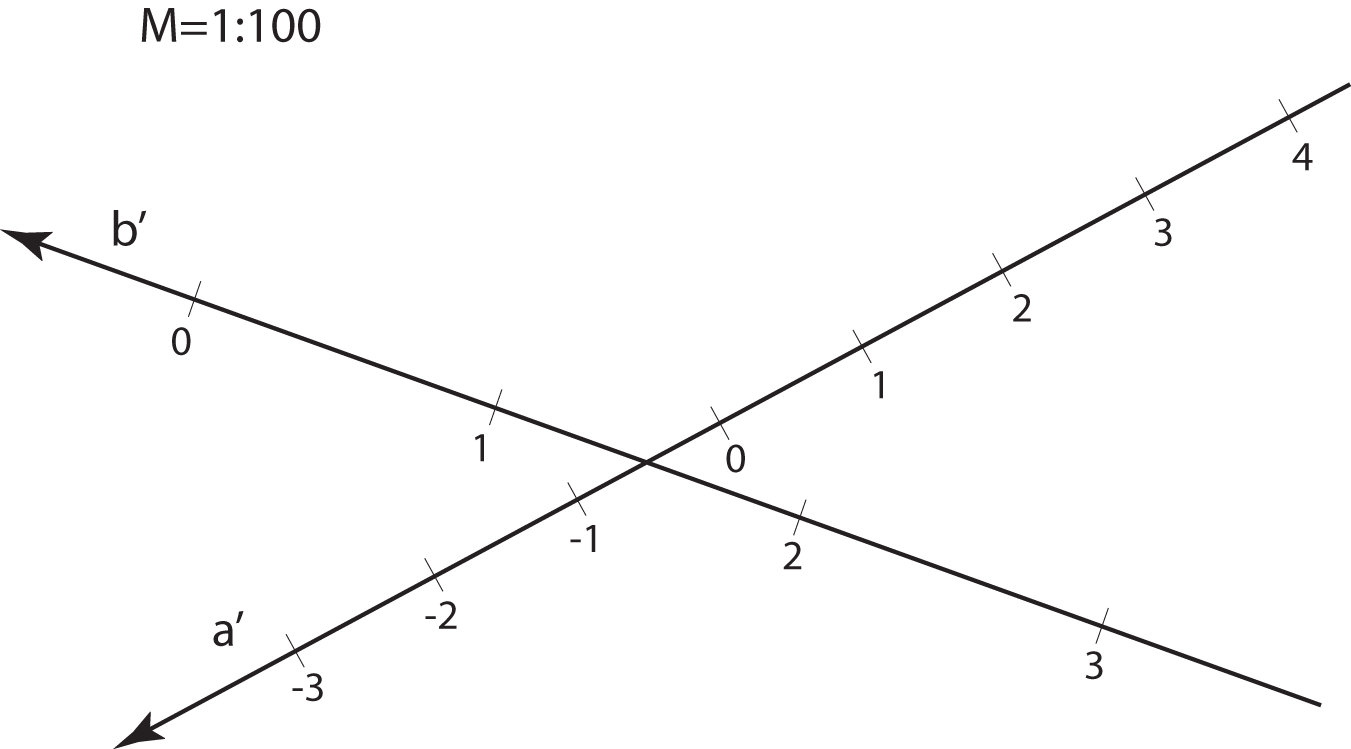
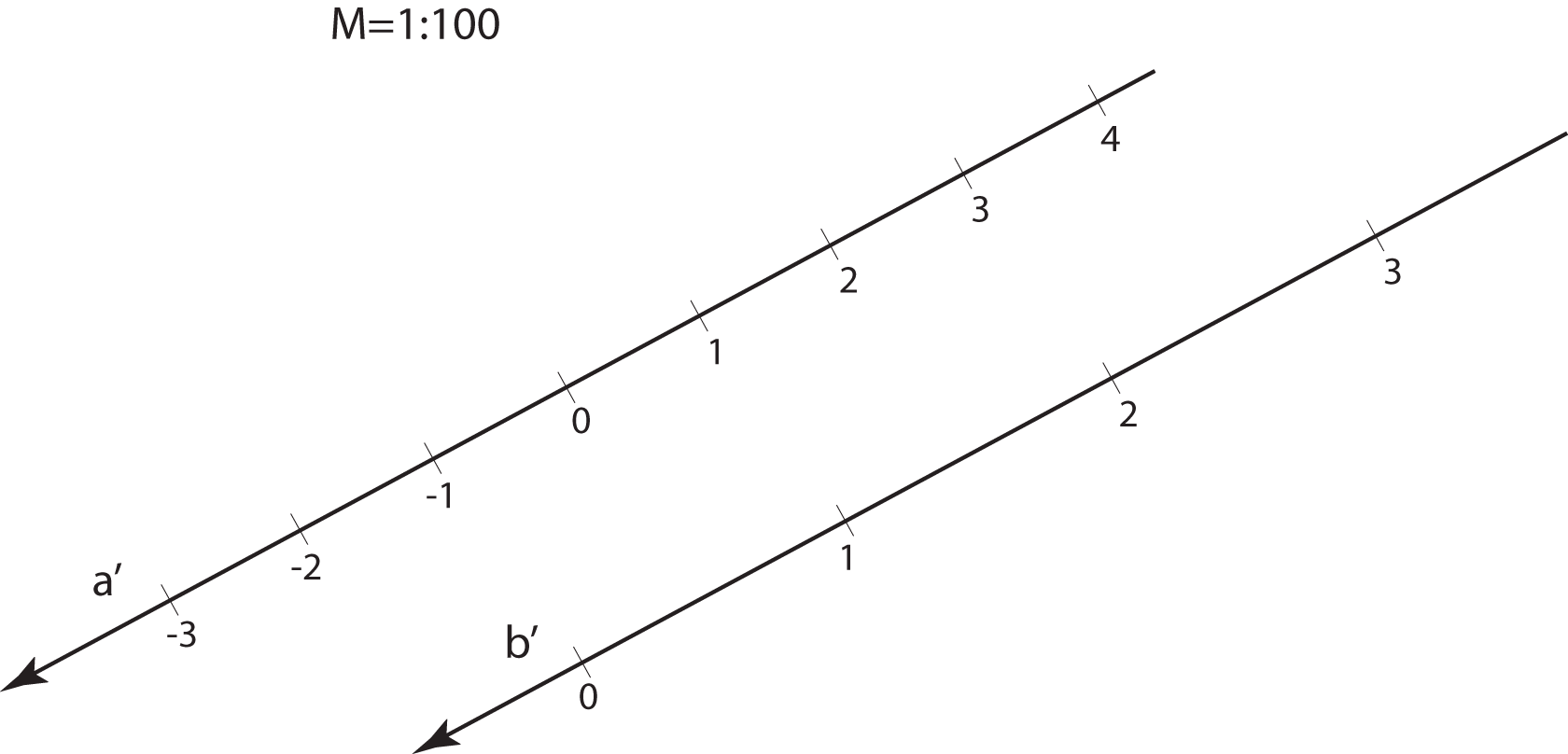
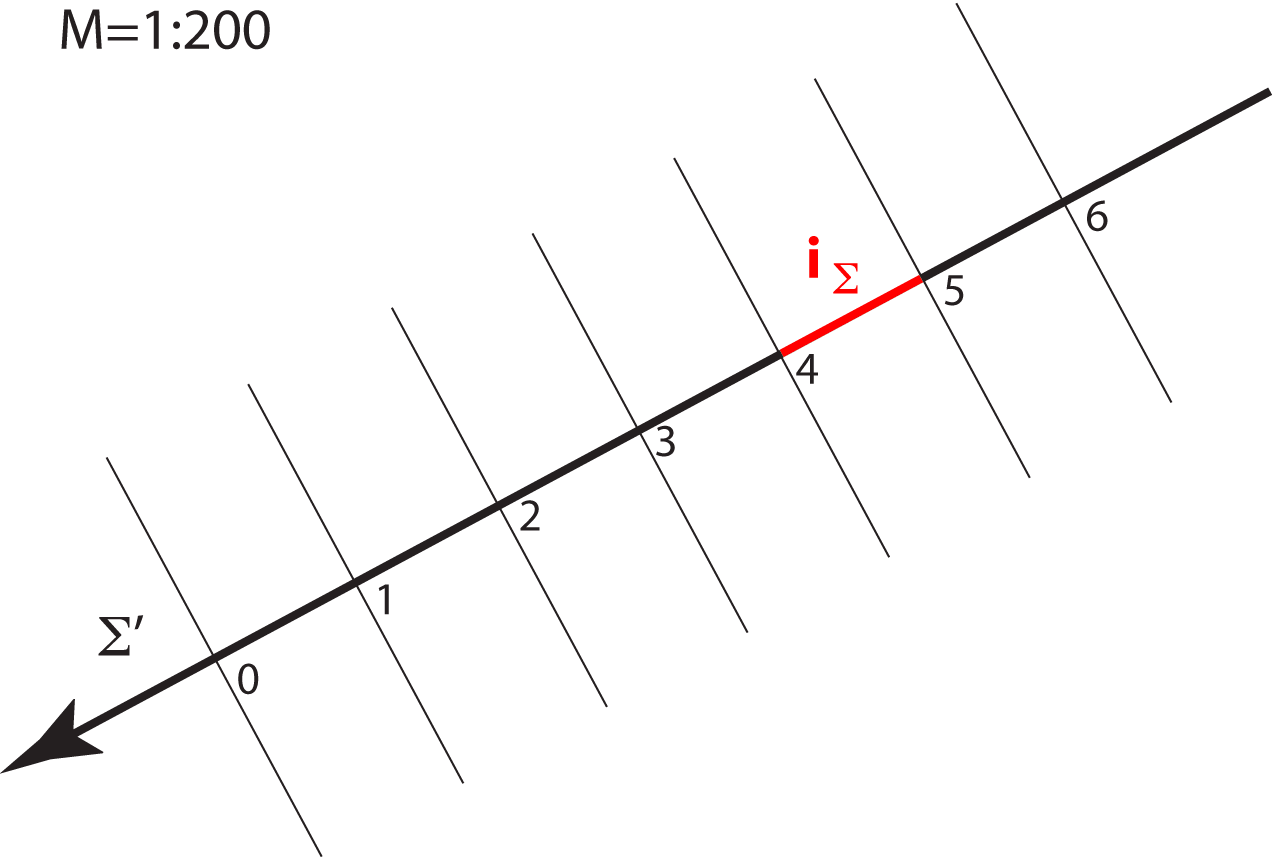
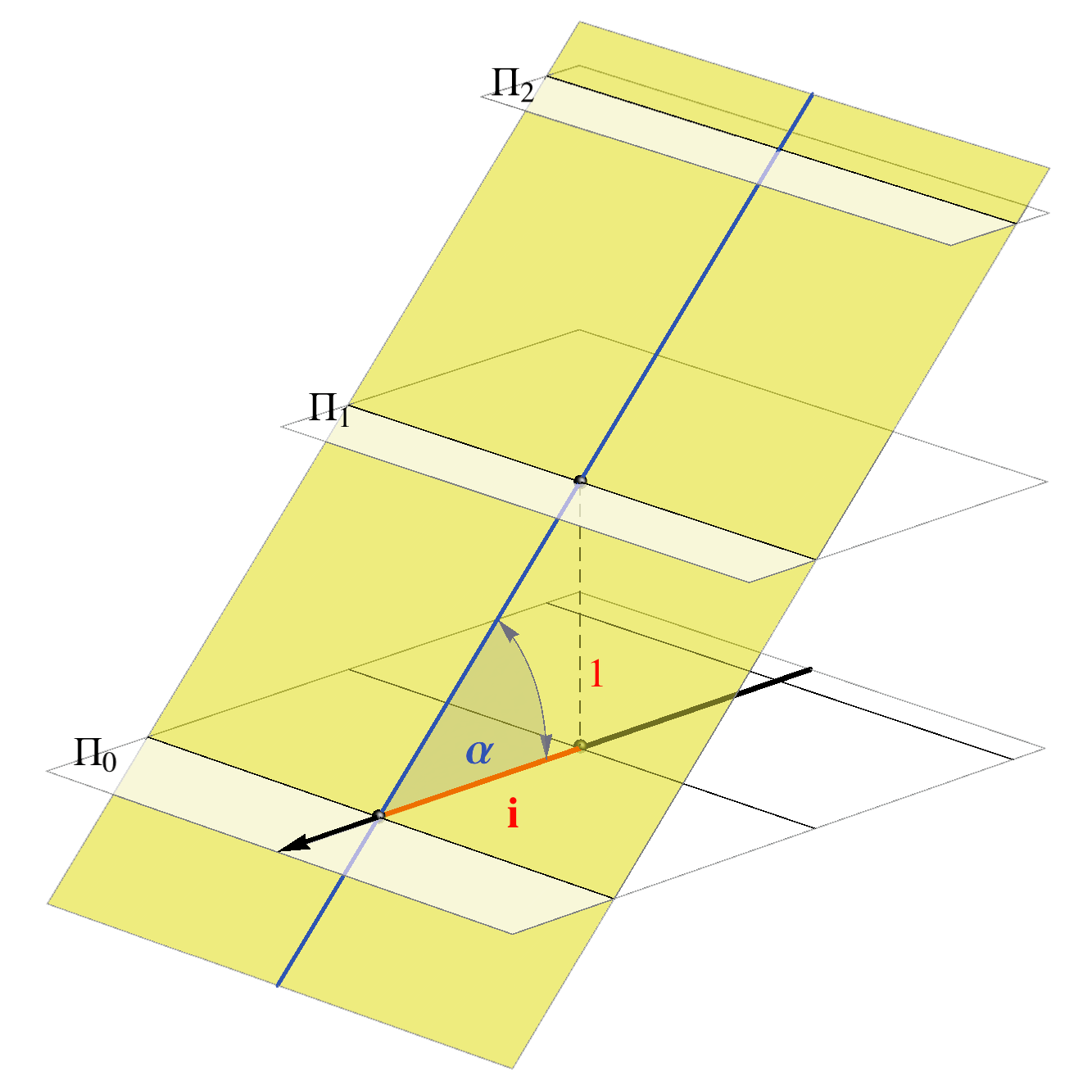
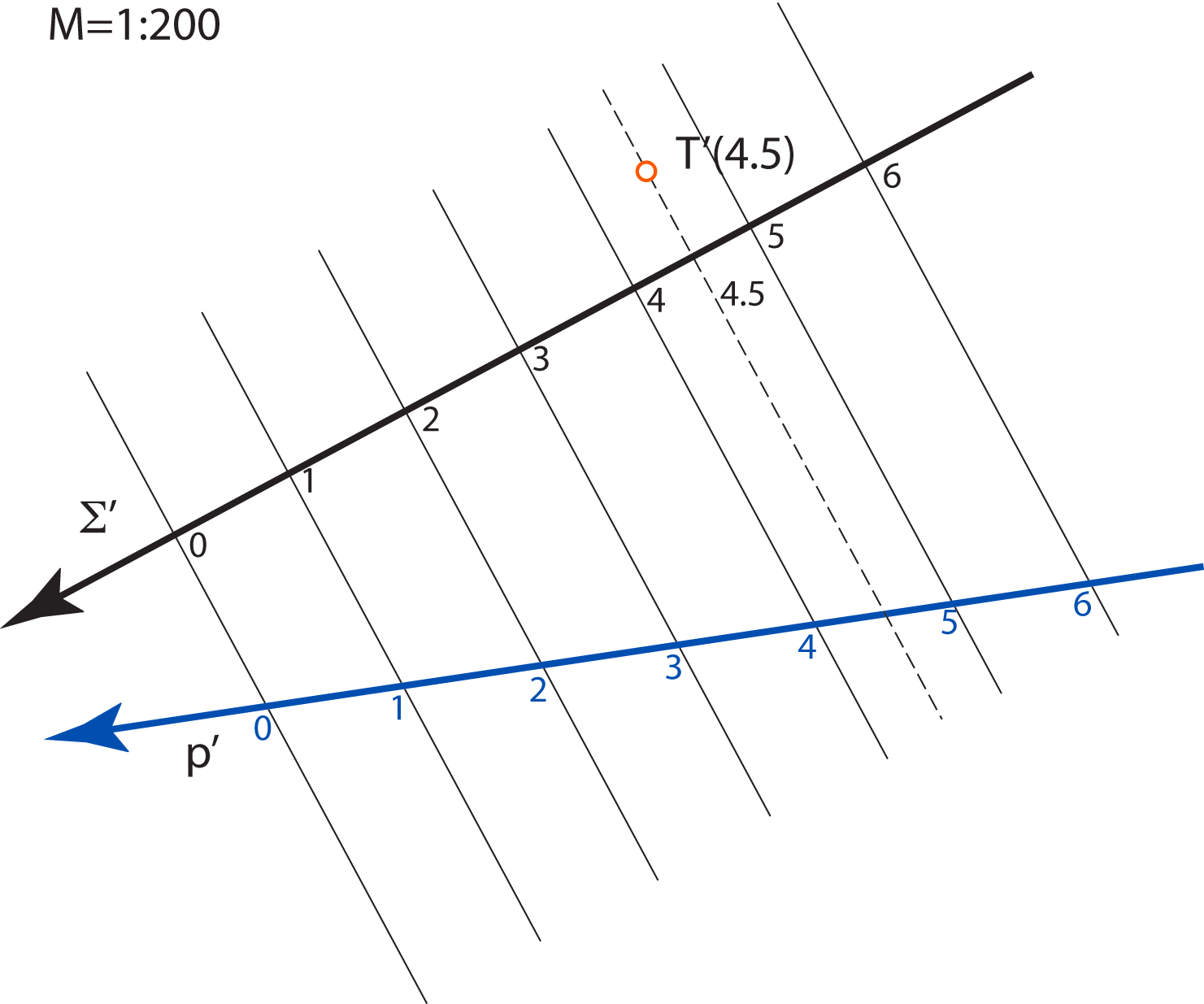
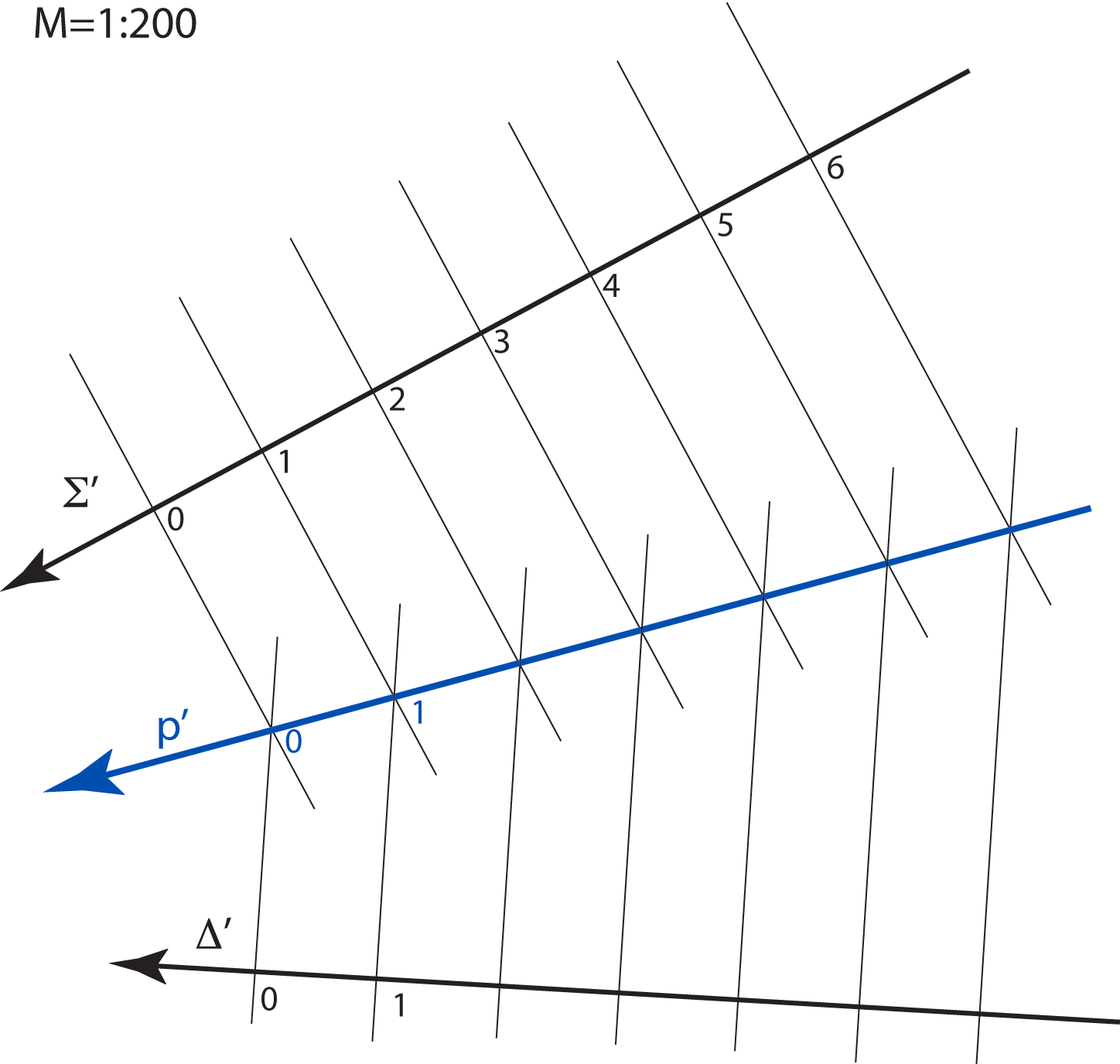
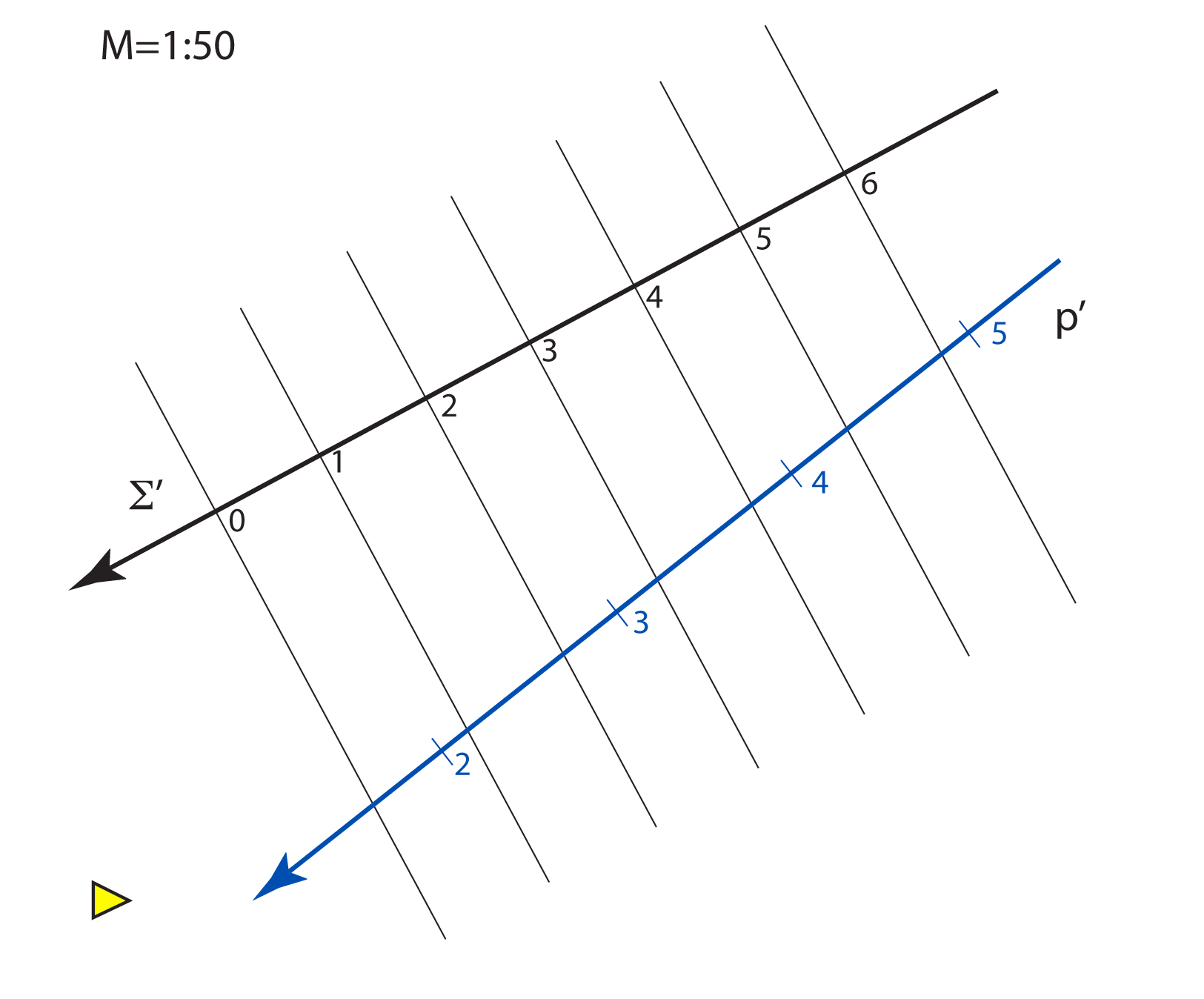
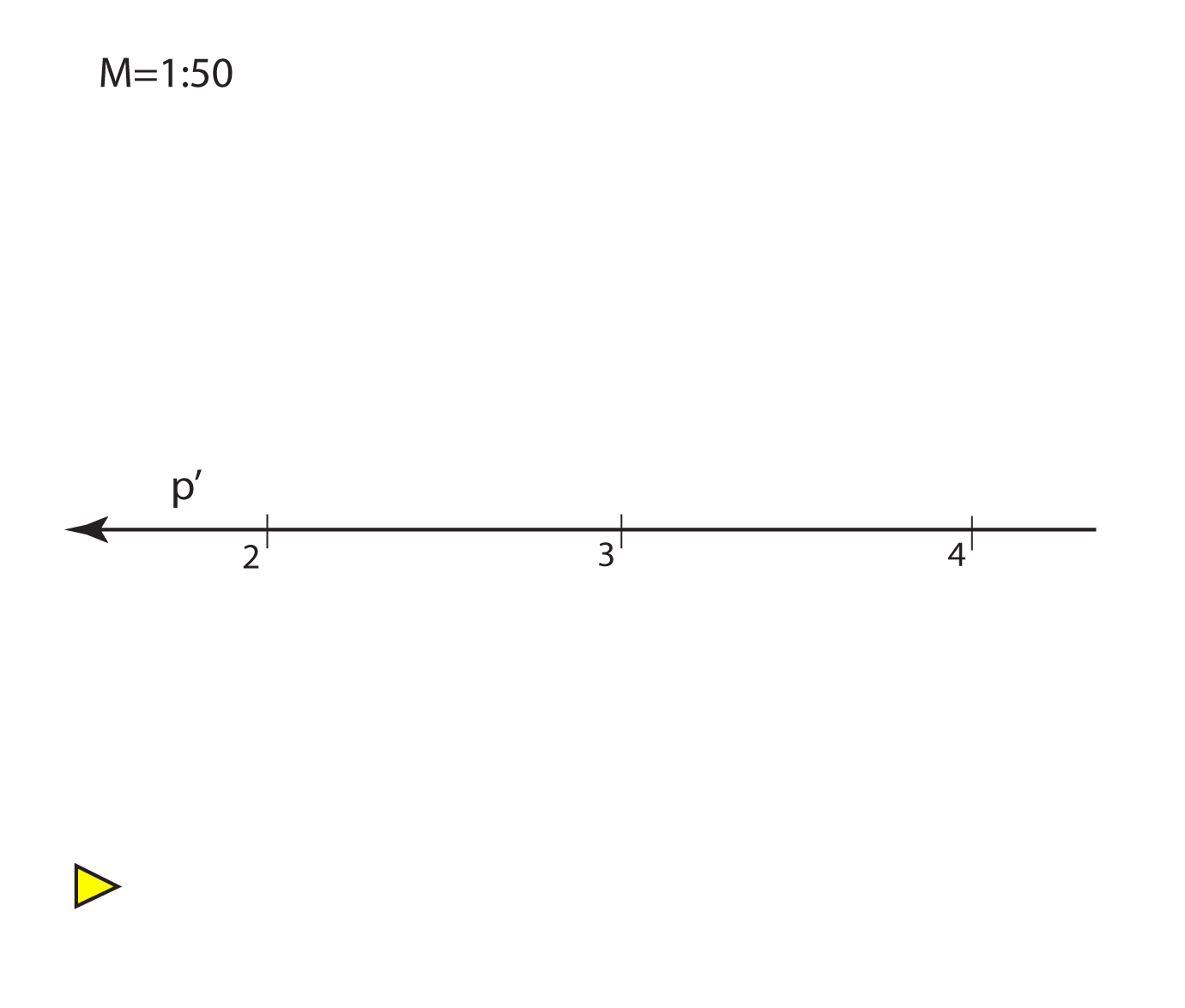
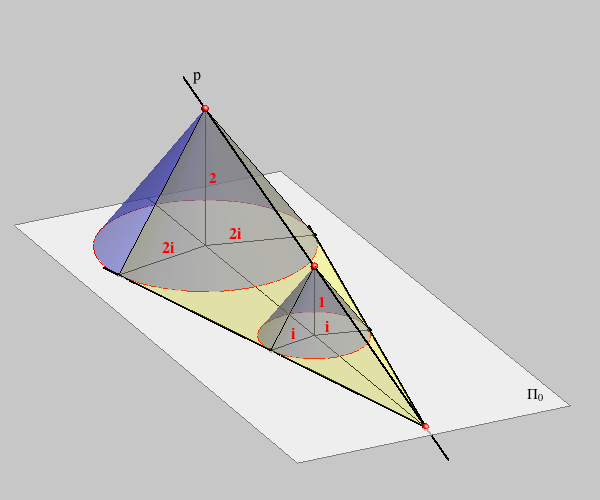
The planes parallel with the projection plane are called level-planes. All points in a level-plane have the same distance from the projection plane and therefore the same elevation.

Specially, the planes with the integer elevation are called main level-planes.
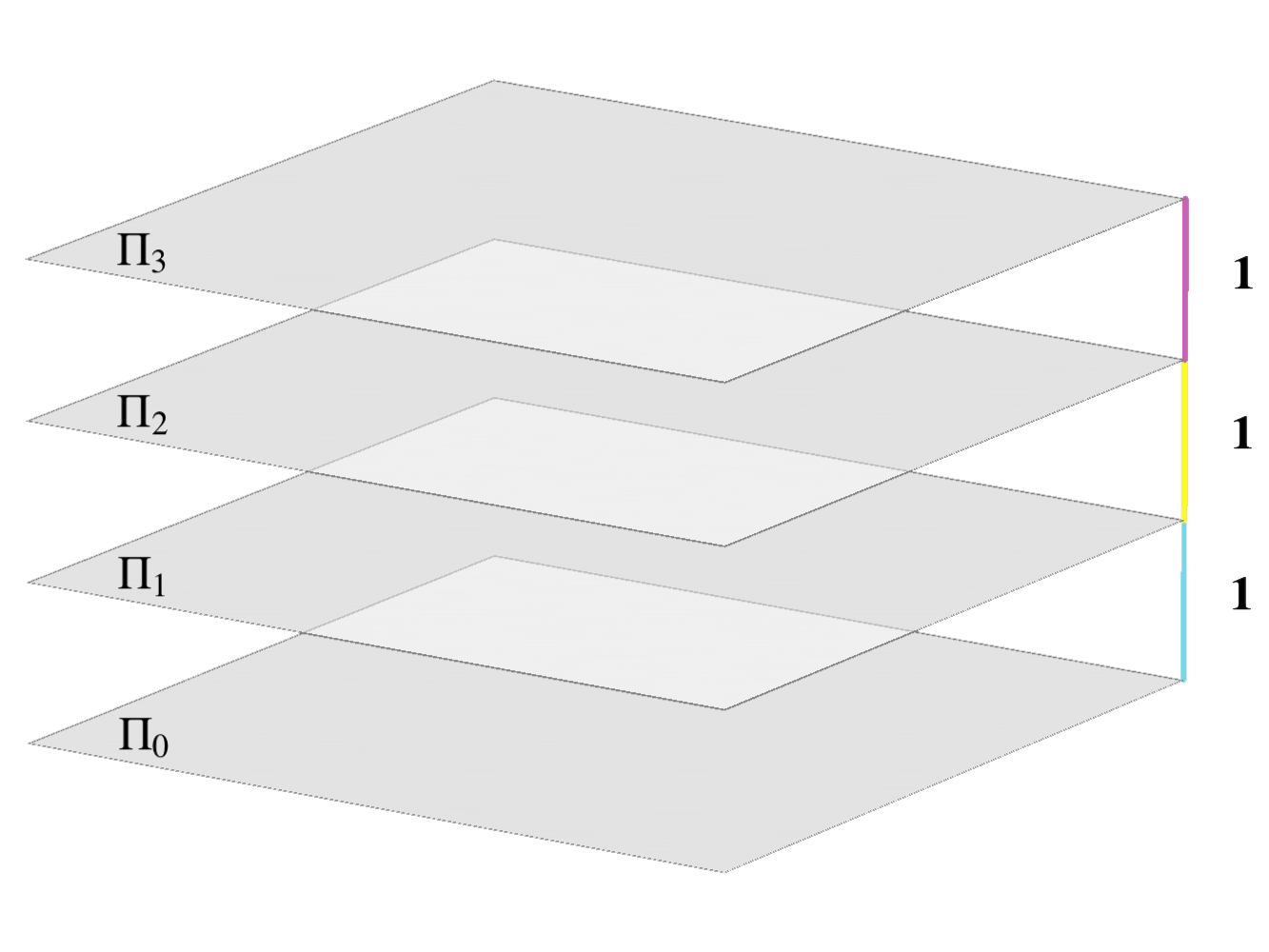
Main level-planes.

The scale

The elevation, i.e. the number that represents the distance between points and the projection plane has to be given in a unit of measurement.
In the elevated projection the elevation is usually given in meters.

Obviously with the chosen unit, it is not possible to draw in true size on a paper.
Therefore, objects in elevated projection are drawn in a smaller scale called the picture scale.

The picture scale is given numerically as a ratio \(\mathbf {M=1:a}\),
which means that the true length of a line-segment which is \(1 m\) long is depicted with the length of \(\frac{1}{a}\,\,m\).

The picture scale has to be defined on every drawing of the elevated projection.

CALCULATE the length of \("1 m"\) in the following picture scales:
\( M=1:25\), \( M=1:50\), \( M=1:100\), \( M=1:125\), \( M=1:200\), \( M=1:250\), \( M=1:400\), \( M=1:500\).

Elevated projection of a point

In the elevated projection a point is represented by its orthogonal projection on the projection plane and its elevation.
The elevation of a point represents the distance between the point and the projection plane given in meters.
In our examples the projection plane will always be the horizontal plane.

The point A is 2m below and the point B is 3m above the projection plane.


Elevated projection of a straight line

A line, in general position to the projection plane, is represented with its horizontal projection and with the points on it that have integer elevations.
These points are called the main points of the line, and such a representation of a straight line is called graded line.
The direction of the fall of a line is indicated with an arrow.

The distance between the projection of two neighbour points with integer elevations, i.e. the horizontal equivalent of a straight line corresponding to the
height difference of 1m, is called the interval of the straight line.
It is obvious that all intervals of a straight line are equal.

The slope of a straight line is the tangent of the angle between the line and the projection plane.

  • The interval and the slope of a line are reciprocal numbers.

    This fact can be easily deduced from the figure below.


    Graded straight line with the indicated interval.



    \( n_p = \tan\alpha = \frac{1}{i}\)




    EXERCISE 1: Grade the line passing through the points A and B.
    To solve this task we need to rotate the line into the projection plane. This construction is the same as the one in Monge's projection for determining the true length of a line segment,
    except that the distance from the projection plane is given with elevation and not with the vertical projection.

    The position of two straight lines

    Intersecting straight lines - the intersection point has the same elevation on both straight lines.

    Parallel straight lines - the projections are parallel and they have the same direction of the fall and same intervals.




    Skew straight lines - intersecting projections lines with different elevations of the intersection point on given lines.

    Skew straight lines - parallel projections with different intervals.

    Straight lines in a special position with respect to the projection plane

  • If a line is perpendicular to the projection plane (ray of the projection), then its interval is 0 and its projection is a point.

  • If a line is parallel with the projection plane, then its points have the same elevation. Hence, the interval is not defined.


    In general, in the elevated projection a line on which lie points with the same elevation has a special role. If the points lie on a surface, then those lines are called
    the horizontals or contour lines of the surface. If the surface is a plane, then its horizontals are straight lines parallel with the projection
    plane. In Monge's projection those lines were called the horizontal principal lines.

    Elevated projection of a plane

    In elevated projection a plane is determined by its projection of the main horizontals and scale of slope.

    Main horizontals are horizontals of the plane which contain points with integer elevation.
    A scale of slope or scale of a dip is any straight line of the plane that is perpendicular to the horizontals of the plane. In terms of Monge's projection it is the 1st steepest line of the plane.

    Slope and interval of the plane are equal to the slope and interval of its scale of slope.

    Main horizontals, scale of slope and indicated interval of the plane.



    Main horizontals are the intersection of the plane and main level-planes.


  • A point lies in a plane if it lies on a horizontal of the plane.
  • A line that lies in a plane is graded with the main horizontals of the plane.



  • The projection of the intersection line of two planes is a line passing through the intersections of the horizontals with the same elevation.



    EXERCISE 2: Construct the projection of the intersection of line \(p\) and plane \(\Sigma\).
    The construction is the same as the one in Monge's projection, except that the horizontal (vertical or profile) projecting plane is not chosen for the auxiliary plane.



    Exercise 3: Construct few horizontals and the scales of slope of the planes which contain the given straight line \(p\) with the slope \(n=2\).
    This exercise will be very important for solving tasks on terrain - the construction of the embankments and excavations for a straight inclined road.





    Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb