A general principle for the construction of points of the intersection of two cones



A general principle for the construction of points of the intersection of two surfaces uses the method of cutting planes. We choose a system of planes and look at the intersections of these planes with the surfaces. Take a plane from this system. This plane intersects each surface at a plane curve and two such plane curves intersect at the points which lie on both surfaces. These points are points of the intersection curve that lie in the chosen plane.

We choose the system of the planes so that the intersections with the surfaces are as simple as can be to enable us to construct many points of the intersection curve.
The constructions are done with ruler and compass, so the most favorable plane intersections are straight lines and circles.

To construct the points of the intersection of two cones we choose a system of cutting planes that intersect both cones along their generatrices.

A plane through the vertex of a cone intersects that cone in two generatrices. Therefore, the system of planes that intersect both cones in their generatrices is a pencil of planes that contain the line through both vertices of the cones.

Every plane of that pencil intersects each of the two cones in two generatrices. These generatrices intersect in 6 points. Four points which are intersections of these four lines, different from the vertices of the surfaces, are points on the curve of intersection. 		right-click \( \rightarrow \) PLAY
The construction of the intersection curve is detemination of all real points of that curve.

The cutting plane can intersect a cone in two real and different generatrices, in one generatrix when the plane is a tangent plane and in two imaginary generatices.

If a cutting plane intersects both cones in one real generatrix, this plane is a common tangent plane and the intersection of these two generatrices is a double point of the intersection curve (as is shown in the figure).

Examples of the intersection of two cones

Proper curves of the 4th order

If one cone passes only partially through the other cone and on both cones exist generatrices that do not intersect the other cone in real points, then the intersection curve is one-branch. This kind of intersection curve is called partial intersection. If one cone passes completely through the other cone and all generatrices of that cone intersect the other cone in two real points, then the intersection curve is two-branch. This kind of intersection curve is called complete intersection.

PARTIAL INTERSECTION - a one-branch curve
COMPLETE INTERSECTION - a two-branch curve


Two cases when the intersection curve has a double point:



When two cones have a common tangent plane in a common regular point, that point is a double point of the intersection curve. If one cone passes through a double point of the other cone, its vertex, that point is a double point of the intersection curve.

an intersection curve with a DOUBLE POINT
In this double point the cones have the same tangent plane.
an intersection curve with a DOUBLE POINT
Double point is a vertex of one of the cones.


Degenerated curves of the 4th order



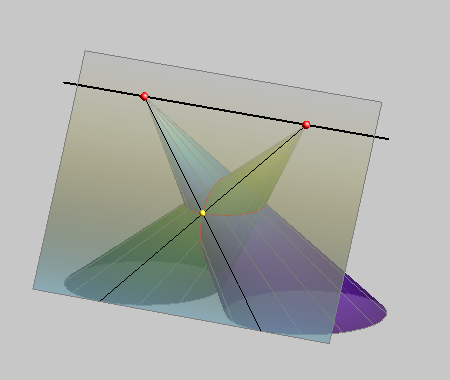
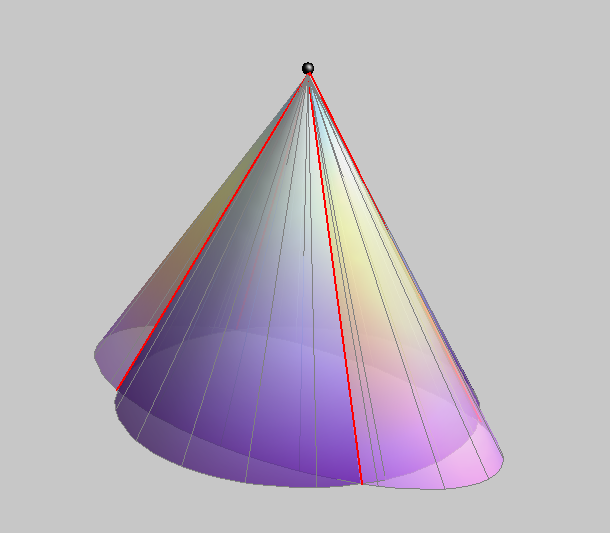
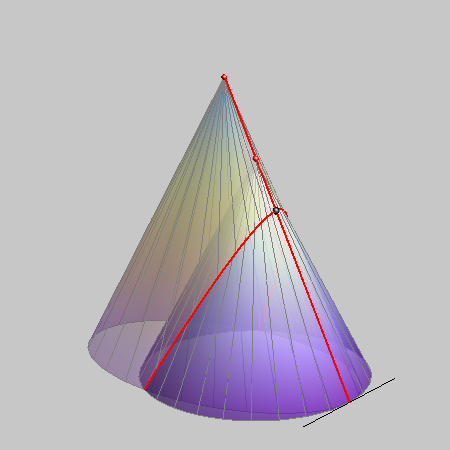
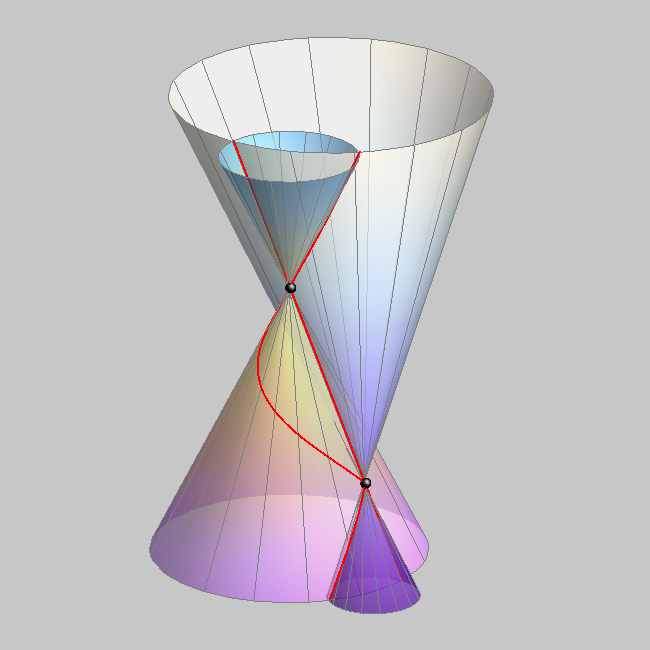
The case of total degeneration into 4 lines appears when two cones have the same vertex.
In that case, the two cones have 4 common generatrices that pass through the common vertex and through the four intersections of the base curves of the cones.
These four intersections can be real and different, real and coincide or pairs of conjugate imaginary points and their type determines the type of generatrices.

Every two cones with a common vertex intersect at four lines that pass through the vertex.

The intersection curve of two cones can never degenerate into two different lines and a conic because in that case the intersection point of the two lines would be the vertex of the cones. As we have seen, if the cones have a common vertex, their intersection curve degenerates into 4 lines.
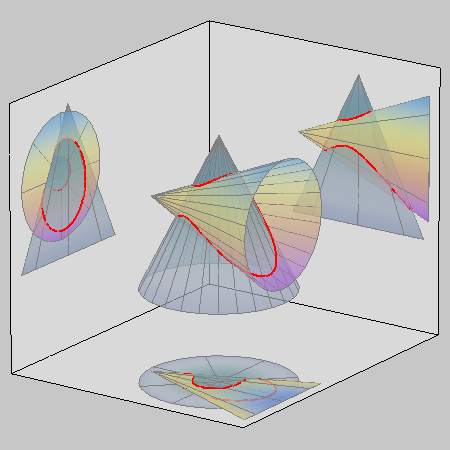
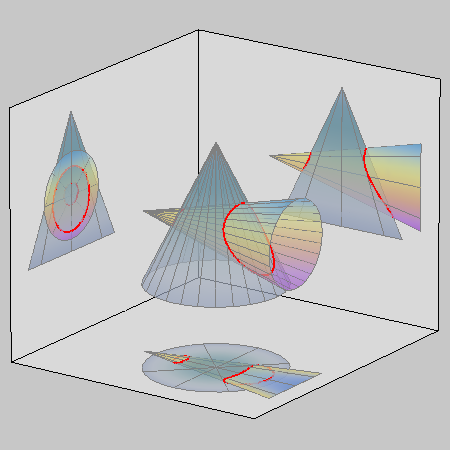
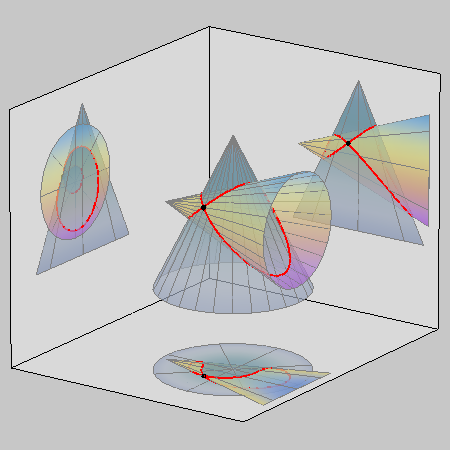
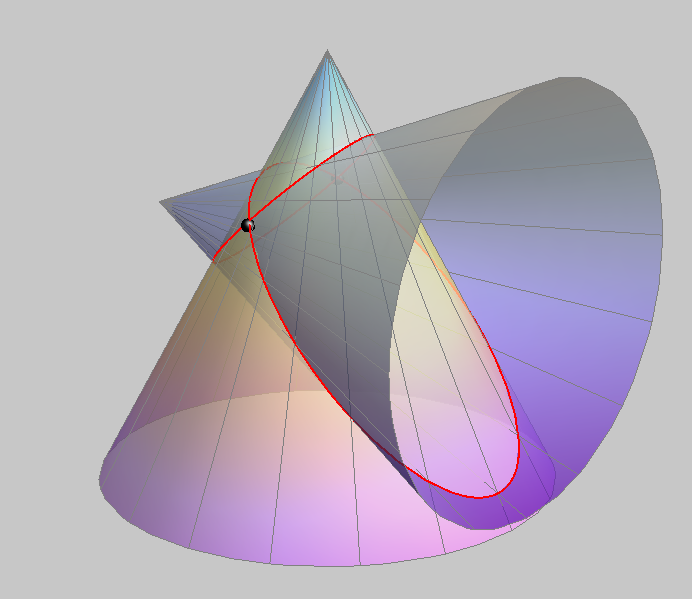
However, if the two cones have a common generatrix and a common tangent plane along that generatrix, then this generatrix is a line counted twice that appears in the degeneration of the intersection curve, together with a conic.

When two cones have different vertices but one common generatrix with a common tangent plane along that generatrix, then the intersection curve degenerates into a double line and a conic.


four lines
a double line and a conic


If two cones have one common generatrix but different vertices and different tangent planes along that common generatrix, then their intersection curve degenerates into a line and a curve of the 3rd order.


If two cones have two common tangent planes but different vertices and do not have a common generatrix, then their intersection curve degenerates into two conics.
If the cones are cones of revolution, this kind of degeneration of the intersection curve appears only if their axes are intersecting lines.

a line and a curve of the 3rd order


two conics



Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb