2nd order curves - CONICS

Within our course we will mostly study  the 2nd order curves,  called conics.
They are classified into ellipses (including circles as special case), hyperbolas and parabolas.

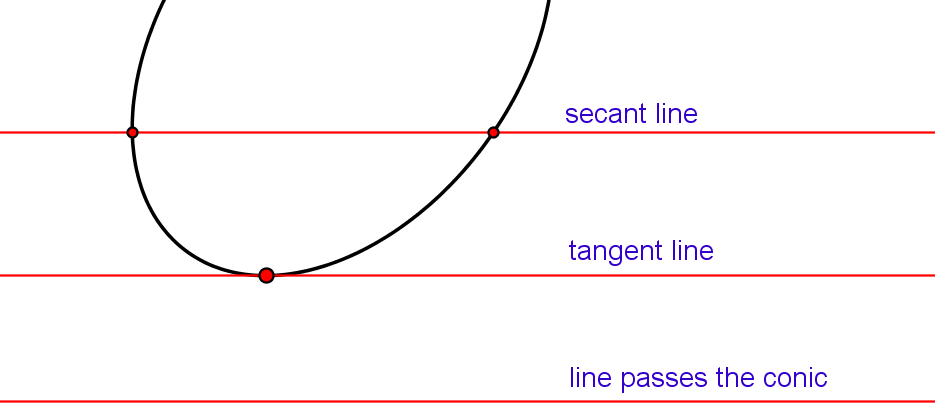
Every line in the plane has 2 intersection points with a conic. If these points are different and real, the line is called secant line. If these two points coincide, the line is called tangent line. If these points are conjugate imaginary points, the line passes the conic. To avoid the notion of imaginary points (that cannot be drawn in the real plane), we say that the secant line intersects the conic in two points, the tangent line in one point of tangency and that the line that passes the conic doesn't have intersection points with the conic.

Figure 5

 The line at infinity of the plane of the conic also intersects the conic in two points. We classify conics based on the type of this intersection:

A hyperbola is a conic that intersects the line at infinity at two real and different points, i.e. the line at infinity is a secant of the hyperbola.
Asymptots of the hyperbola are the tangent lines in these points at infinity.  

A parabola is a conic that intersects the line at infinity in one point (two points that coincide), i.e. the line at infinity is a tangent of parabola. This point at infinity lies on the parabola's axis.


An ellipse is a conics that intersects the line at infinity in two imaginary points.
A circle is an ellipse that passes through a special pair of conjugate points of the line at infinity. These points are called absolute points of the plane.

Move the point X in figure 6.

Figure 6

Image 6 demonstrates intersection points of conics with the line at infinity. These points are easy to imagine when they are real, but it is impossible to draw them. Imaginary points at infinity are very hard  even to imagine. But they can influence real parts of the conics. As an example, answer the following question: Why do two circles have at most two common real points?

Figure 7

Plane algebraic curves can be sorted not just by their degree, but also by class of the curve.

Class of a plane algebraic curve equals the number of tangent lines to the curve from any point of the plane of the curve.

Tangents to the curve can be real but can also be conjugate imaginary. Imaginary lines are very hard to imagine, just like imaginary points. We state that all conics are curves of class 2 - that through any point in the plane we have two tangent lines of a conic. These tangent lines are real and different if the point lies in the exterior of the conic, real but coincide if the point lies on the conic and conjugate imaginary if the point lies in the interior of the conic. If the degree and the class of the algebraic curve coincide, than we say that curve has order. Conics are 2nd order curves.

Move the point X in Image 8 to observe in which areas we have two real tangents or two imaginary tangents. In the boundary of these areas are the points that give unique tangent; but it is counted twice in the determination of the class of the curve.

Figure 8

PARABOLA - ENVELOPE of STRAIGHT LINES

All nondegenerate conics (ellipses, hyperbolas, parabolas) have no double points. The expression for the bound of the number of double points  (n−1)(n−2)/2 equals 0 when n=2. If a conic has a double point, than it is decomposed into two lines that can be real and different, real and coincide or a pair of conjugate imaginary lines that intersect in a single point.

Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb, made with GeoGebra