Curvature of a Plane Curve

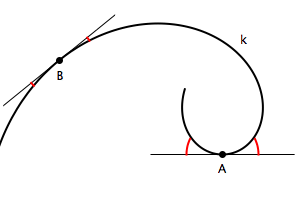
Notion of curvature is very intuitive. For instance, it is easy to say at which point on the curve k is the curvature greater, point A or point B. In differential geometry, the curvature of a curve is calculated using second derivatives of the vector equation of the curve and it is a measure for the angle between the curve and its tangent at a point. In this class we won't use the methods of differential geometry or give its physical interpretation. We will give a constructive method of determining curvature that uses osculating circles of conics. Figure 14 at the bottom shows this construction.

Curvature of a circle c of radius R is the same for all points on the circle and equals κ_c=1/R.

The circle is a curve of constant curvature, and we will use it to determine the curvature of other curves. When the radius of a circle gets smaller, the curvature is greater. Curvature of a straight line equals 0, and it can be interpreted as curvature of a circle with infinitely big radius.  

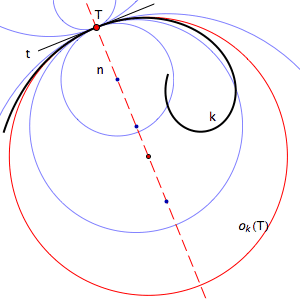
Let T be a regular point of a curve k. Any circle that contains T and has its center on the normal line of k at T must have the same tangent line as k at T. Every circle with this property intersects the curve k at two points that coincide with T. We say that the curve and the circle have tangency of 1st order at T, and the circle is called tangent circle at T.  Curve k has infinitely many tangent circle at the point T (this number equals the number of points on the normal line at T) and this circles form a pencil of tangent circles of k at T. If k is an algebraic curve of order n, each tangent circle will have 2(n-1) common points with k, beside the point T (counted twice).

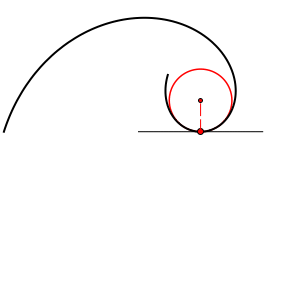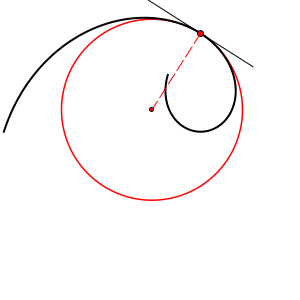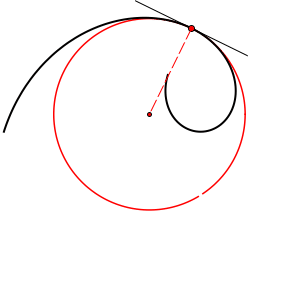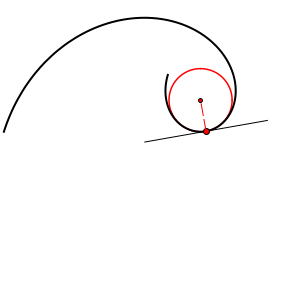
In the pencil of tangent circles, there always exists one circle that has the property that one of the remaining 2(n-1) intersection points also coincide with T (the curve and this circle have 3 common points that coincide with T). In that case, we say that the curve and the circle have tangency of 2nd order at T. This circle is called osculating circle or circle of curvature of the curve k at the point T. We denote it o_k(T).

Curvature of a curve k at a point T equals the curvature of its osculating circle at T, i.e. κ_k(T)=κ_ok(T)

If the curve k is symmetric with respect to the normal line near the point T, then the osculating circle intersects this curve four times at T. In this case, we say that the curve and the circle have tangency of 3rd order, and we say this circle is hyperosculating circle. 

Osculating and hyperosculating circles of conics

Tangent circle of a conic at a point T has 2 intersection points with the conic beside the point of tangency T. These remaining 2 points can be real and different, real but coincide in which case the conic and the circle have 2 points of tangency or they can be conjugate imaginary points. In all these cases, there is a neighborhood of T on the conic such that the arc of the tangent curve lies entirely on the same side of the conic in this neighborhood - in its interior or its exterior.

Osculating circle of a conic is a unique circle for each point T on the conic. In this point T we have 3 intersection points of the conic and the circle so the circle must intersect the conic in one more real point beside T. This intersection point divides the osculating circle in two parts - one is the arc that lies in the interior, and the other is the arc that lies in the exterior of the conic. We can say that the osculating circle is tangent at T but also intersects the conic at T.

Hyperosculating circle of the conic is the tangent circle in a vertex T of the conic. This is because the vertex of a conic lie on its axis of symmetry and this axis of symmetry is also the normal line at this vertex. If the circle is osculating in a vertex of the conic, due to the symmetry, the fourth intersection point must also coincide with the vertex. The conic and this circle have four common points at the vertex so they have no common points beside this point. Therefore, all points of this circle beside T must lie entirely in the interior or the exterior of the conic.
Ellipse has 4 real vertices, hyperbola and parabola 2, but one vertex of parabola is a point at infinity.

Curvature of a conic in its vertex has extreme value.

Figure 11 shows this properties.

Figure 11

Every point of a conic has unique normal line and on this line an unique point that is the center of the osculating circle of the conic. When a point moves continuously along the conic, these centers of osculating circles form an algebraic curve with the property that its tangent line is the corresponding normal line of the conic. This curve is called the evolute of the conic.

Figure 12 shows the evolutes of an ellipse, a hyperbola and a parabola. Try to animate this examples.

Figure 12

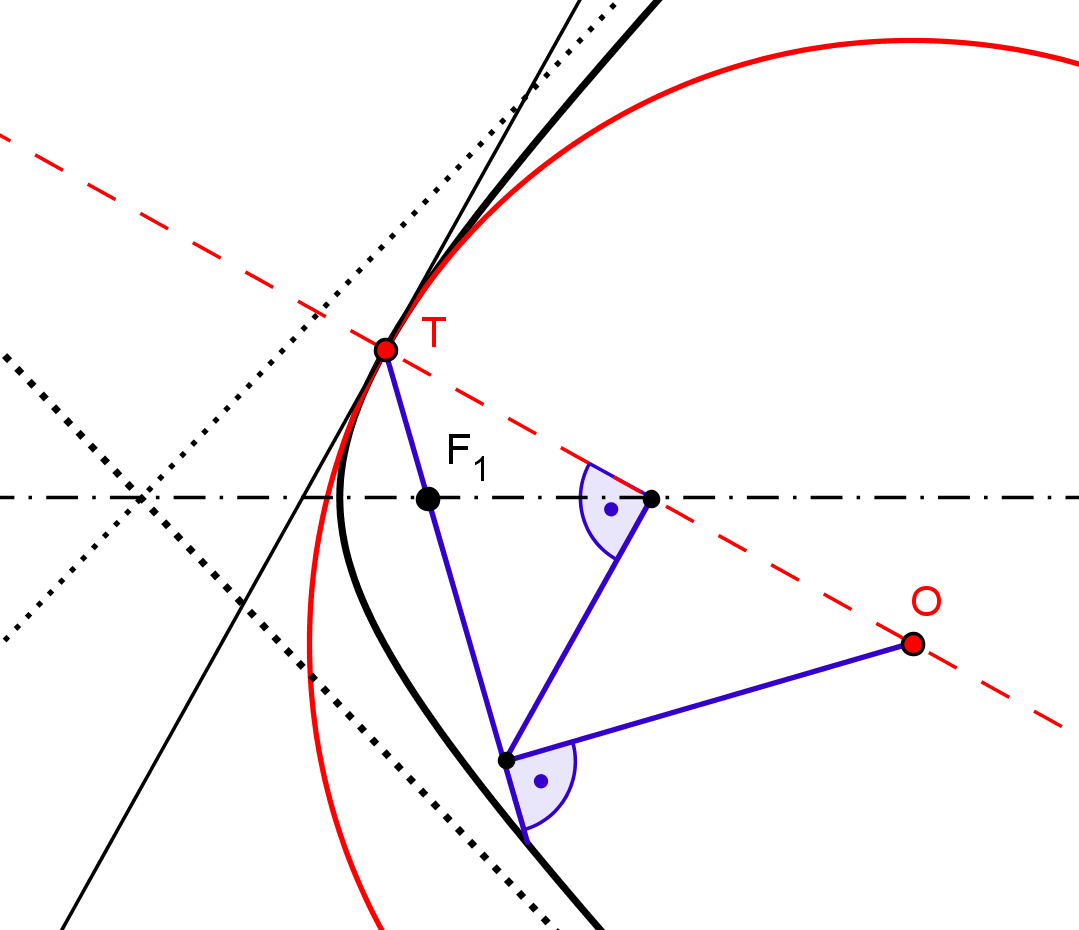
Figure 13 shows constructions of the centers of osculating circles in a point on an ellipse, hyperbola or parabola.

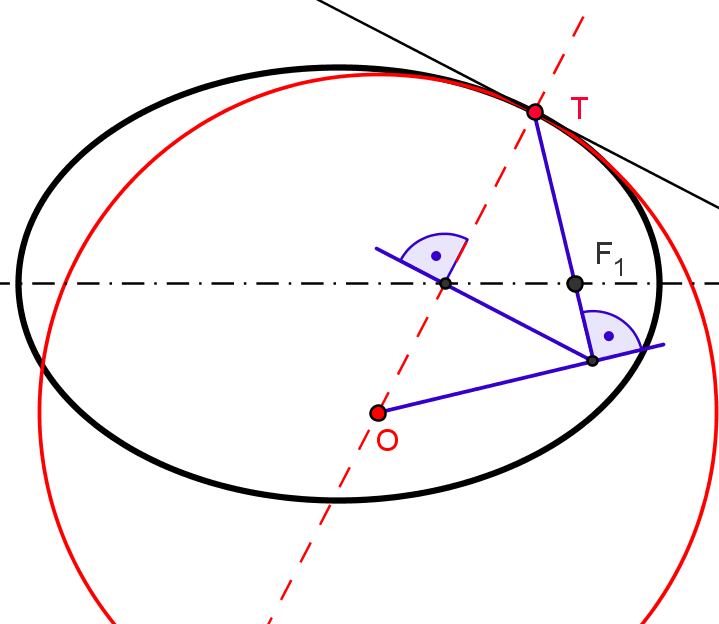
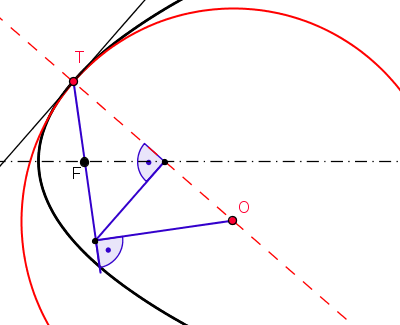
Figure 13

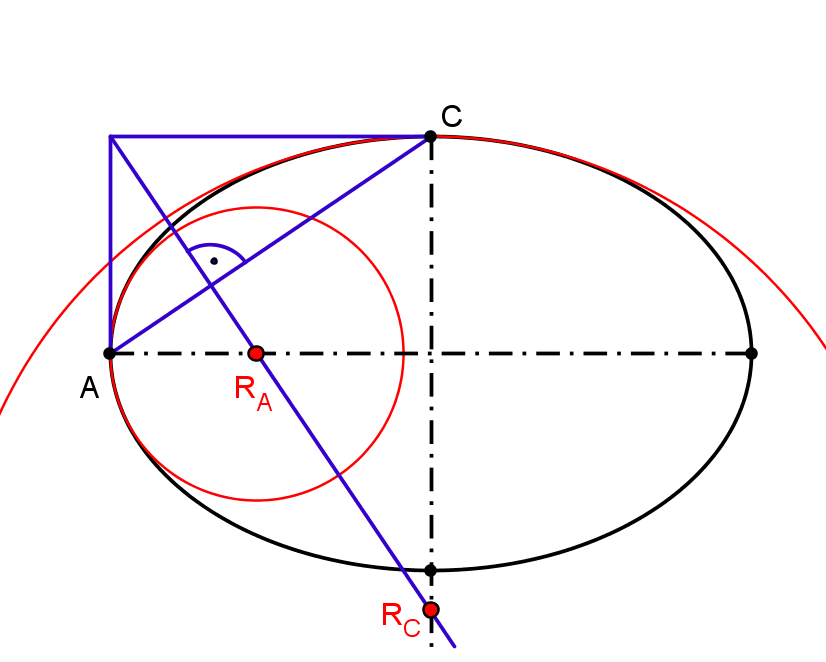
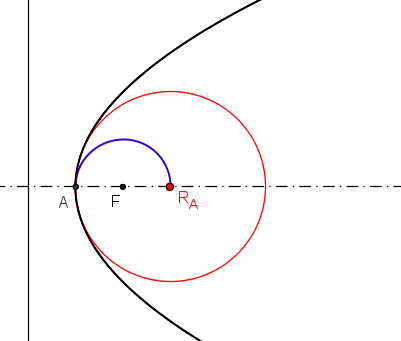
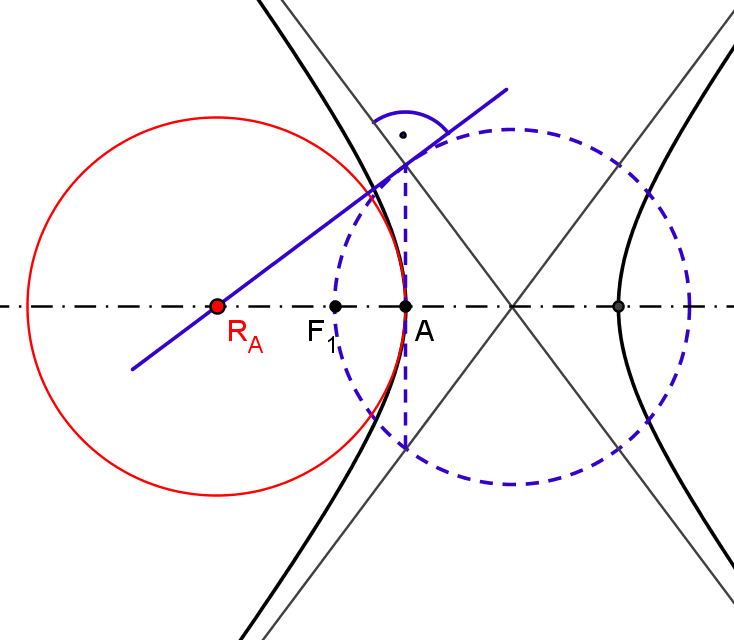
Figure 14 shows constructions of centers of hyperosculating circles in a vertex of an ellipse, hyperbola and parabola.

Figure 14

Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb, made with GeoGebra