Basic geometrical relationships The relative positions of points, lines and planes Two points can coincide or be different. A point and a line can be in these positions: a point T lies on the line p (T ∈ p), a point T doesn't lie on the line p (T ∉ p). A point and a plane can be in these positions: a point T lies in the plane Σ (T ∈ Σ), a point T doesn't lie in the plane Σ (T ∉ Σ). Two lines can coincide or be different. If they are different, they can be in these positions: lines p1 and p2 are intersecting lines, they meet at a point which is their intersection ( p1 ∩ p2 = P), lines p1 and p2 are parallel, they meet at the point at infinity ( p1 || p2, i.e. p1 ∩ p2 = P∞), lines p1 and p2 are skew lines, they have no common points (p1 ∩ p2 = Φ). 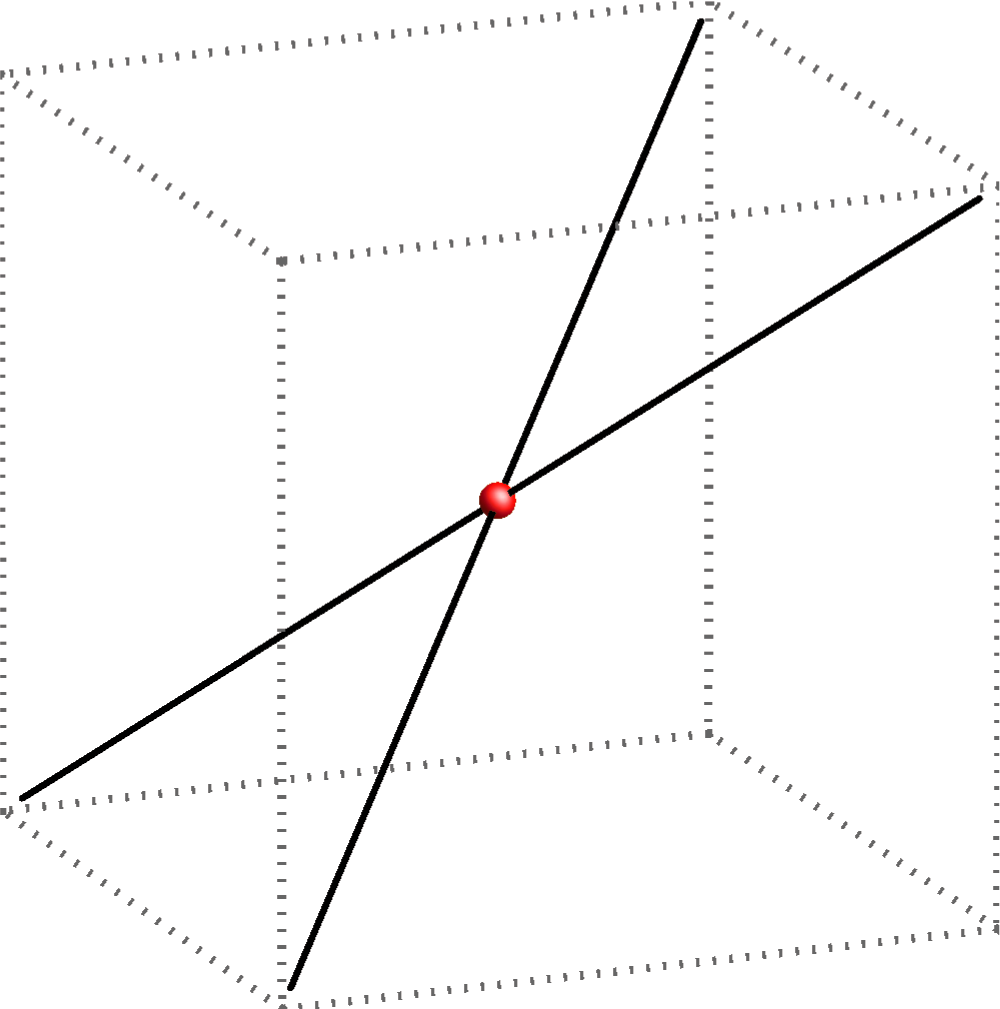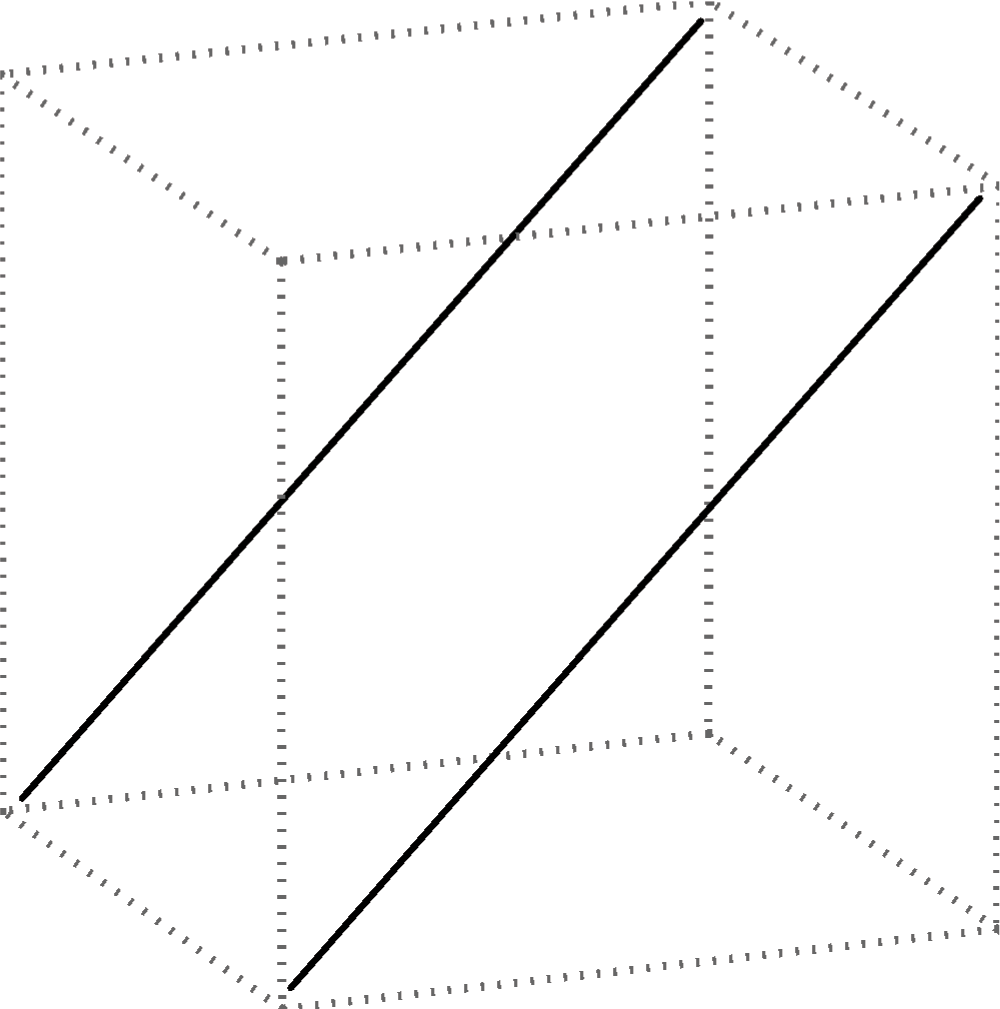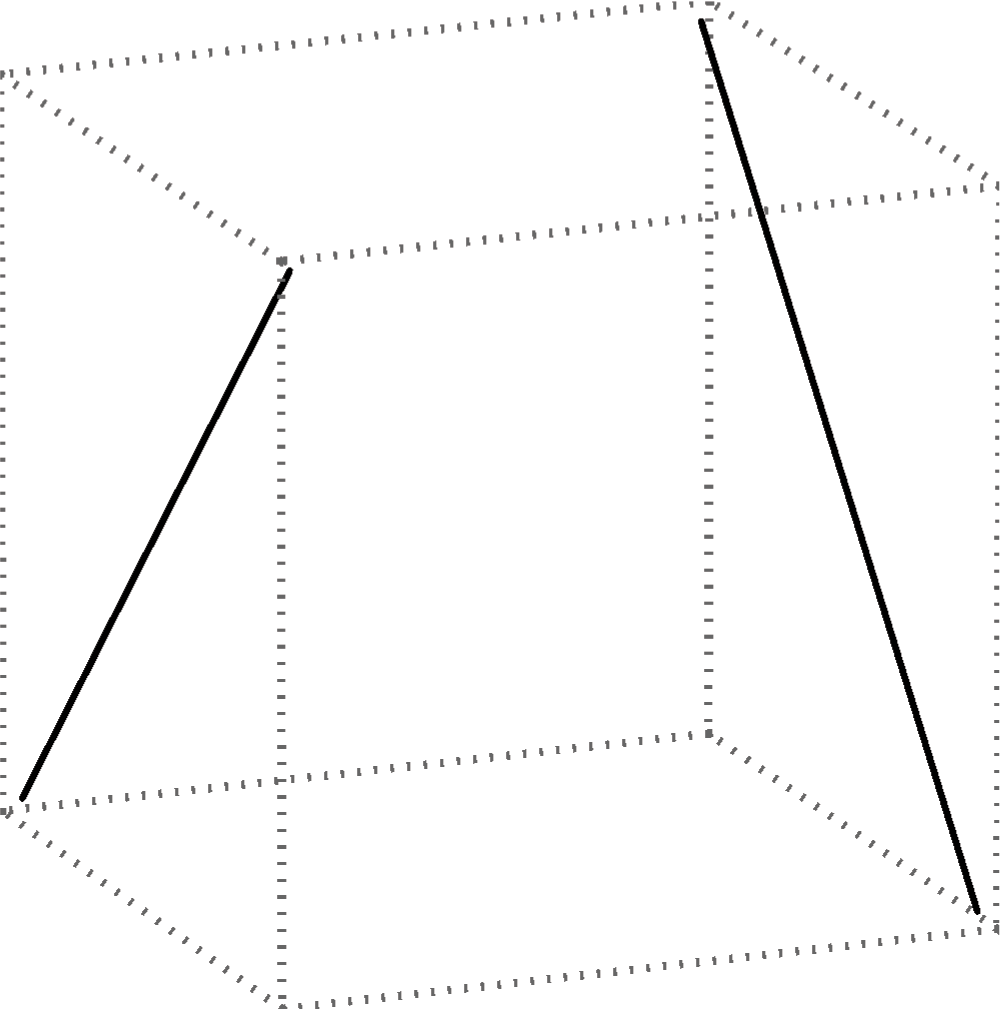intersecting lines parallel lines  skew lines Two planes can coincide or be different .  If they are different, they can be in these positions: planes Σ1 and Σ2 are intersecting, they have one common line called  intersection line (Σ1 ∩ Σ2 = p), planes Σ1 and Σ2 are parallel, their intersecting line is a line at infinity ( Σ1 || Σ2, i.e. Σ1 ∩ Σ2 = p∞). 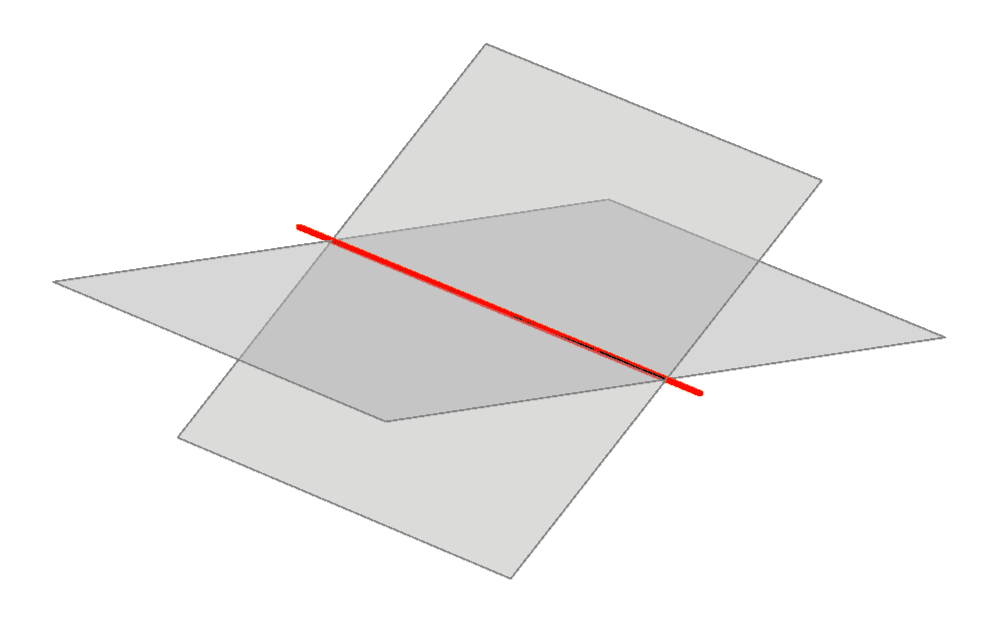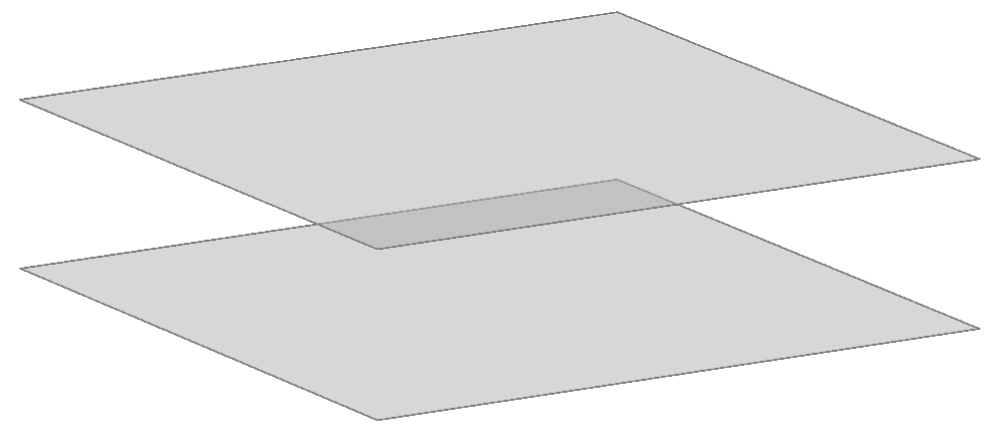intersecting planes parallel planes A line and a plane can be in the following positions: a line p lies in the plane Σ (if two different points on the line p lie in the plane Σ, then the line p lies in the plane Σ, p ⊂ Σ), a line p and the plane Σ intersect, then the line and the plane have one common finite point ( p ∩ Σ = P), a line p and the plane Σ are parallel, they intersect at a point at infinity ( p || Σ, i.e. p ∩ Σ = P∞). A line p is parallel to the plane Σ if Σ contains at least one line parallel to the line p. In that case,  Σ contains infinitely many lines parallel to the line p. They form a pencil of lines.  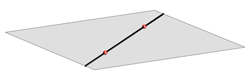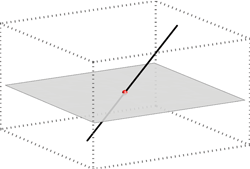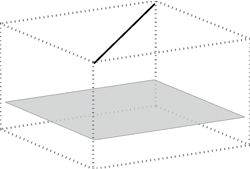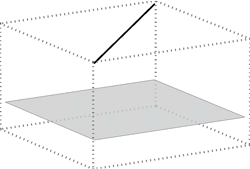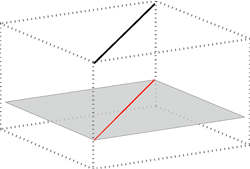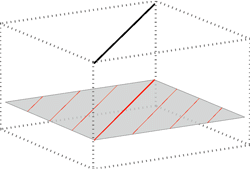line lies in the plane  line intersects the plane  line is parallel to the plane Defining a plane A plane is uniquely defined given: three non-collinear points, one line and a point not on that line, two intersecting lines, two parallel lines. 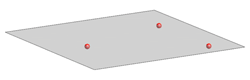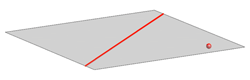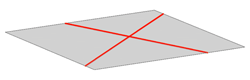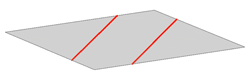Points and lines contained in the same plane are called coplanar. Skew lines cannot be contained in the same plane, they cannot be coplanar. Angle measurement and perpendicularity Angle between lines and perpendicular lines The measurement of the angle between two lines is taught in elementary school. The angle between two perpendicular lines equals 90o (the right angle), and the angle between parallel lines equals 0o. All other angles are between that two numbers. We can also measure the angles between non-coplanar lines in the following way: Let p and q be two skew lines. We pick a point on one of these lines and put a line r parallel to the other line through that point. Now the angle between skew lines p and q equals the angle between these intersecting lines. Two skew lines are perpendicular if the angle (as defined above) is the right angle. 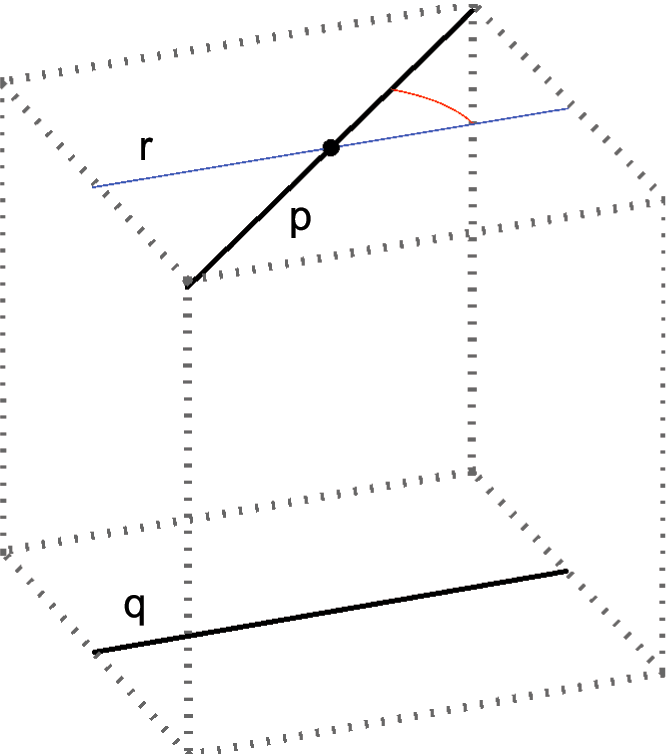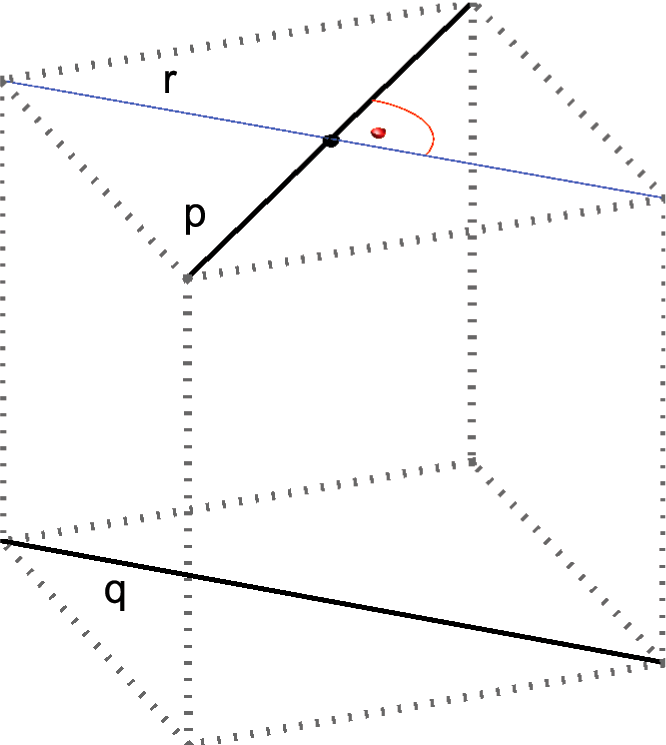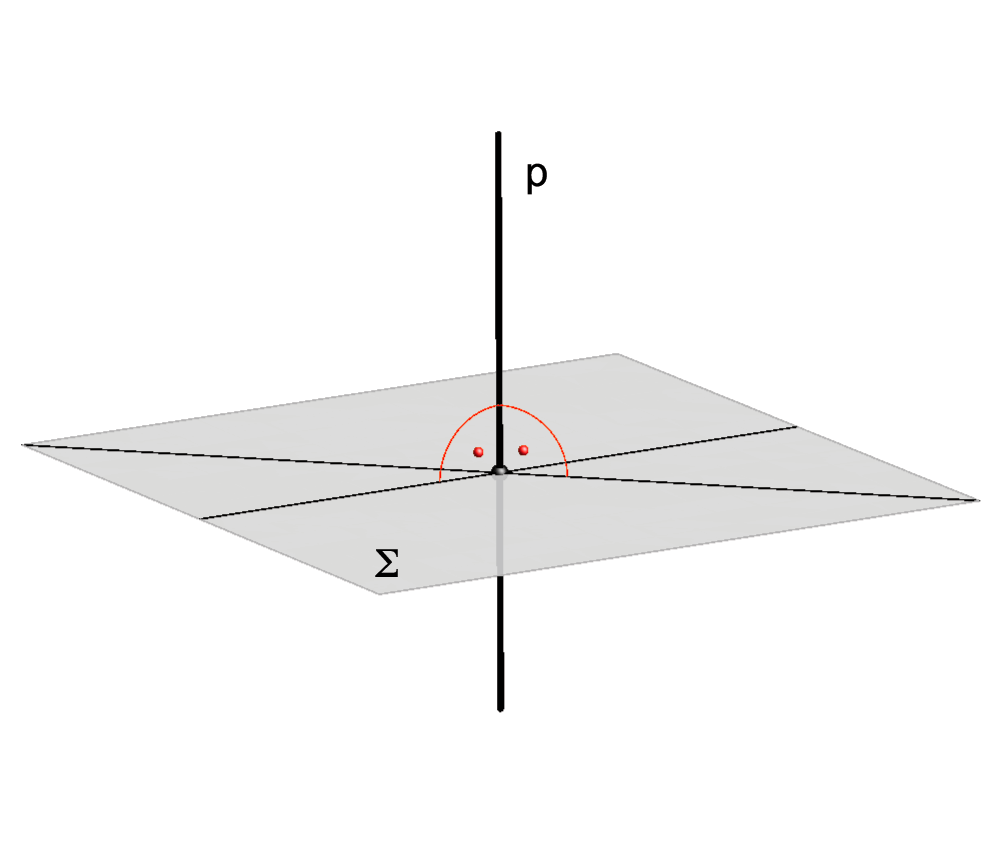q || r, ∠(p,q) = ∠(p,r) q || r, p ⊥ r => p ⊥ q A line perpendicular to a plane A line p is perpendicular to the plane Σ if it is perpendicular to all lines lying in the plane Σ. The line p is then called normal line of the plane Σ, the intersection of the line p and the plane Σ is called perpendicular foot of the line p. It is obviously unnecessary to check perpendicularity to all lines of the plane (and also impossible) so we need necessary conditions for the line to be perpendicular to the plane. These conditions are given in the following theorem: The line p is perpendicular to the plane Σ if it is perpendicular to any two intersecting lines in the plane. Here are another two intuitive and important theorems: Given a line, there is a unique plane through every point of the space that is perpendicular to that line. Given a plane, there is a unique line through every point of the space that is normal line of that plane. A line is perpendicular to a plane if it is perpendicular to two intersecting lines of the plane. 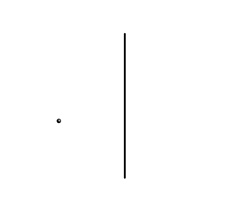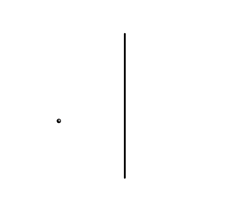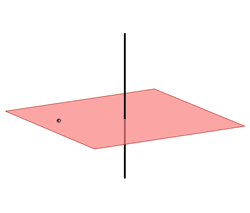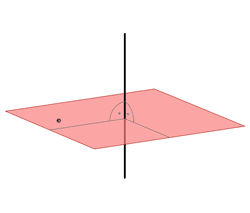A unique plane perpendicular to a given line through any point. A unique normal line of a given plane through any point. Perpendicular planes Two planes are perpendicular if one plane contains at least one line perpendicular to the other plane. This fact can be written: Σ1 ⊥ Σ2 <=> ∃ p ⊂ Σ1, p ⊥ Σ2 Perpendicularity is a symmetrical relation, if Σ1 ⊥ Σ2, then Σ2 ⊥ Σ1, so in the plane Σ2 exists a line perpendicular to Σ1.  Furthermore, if the planes are perpendicular, then each one of them contains infinitely many lines perpendicular to the other plane (pencil of normal lines). 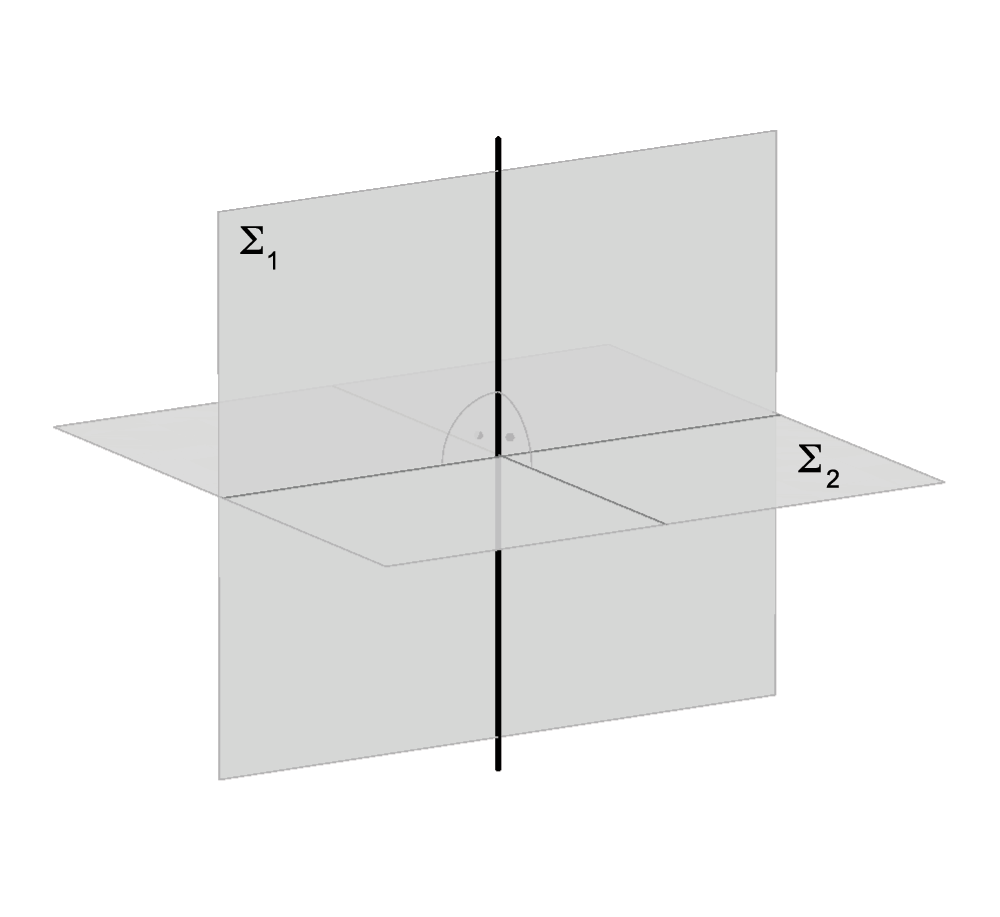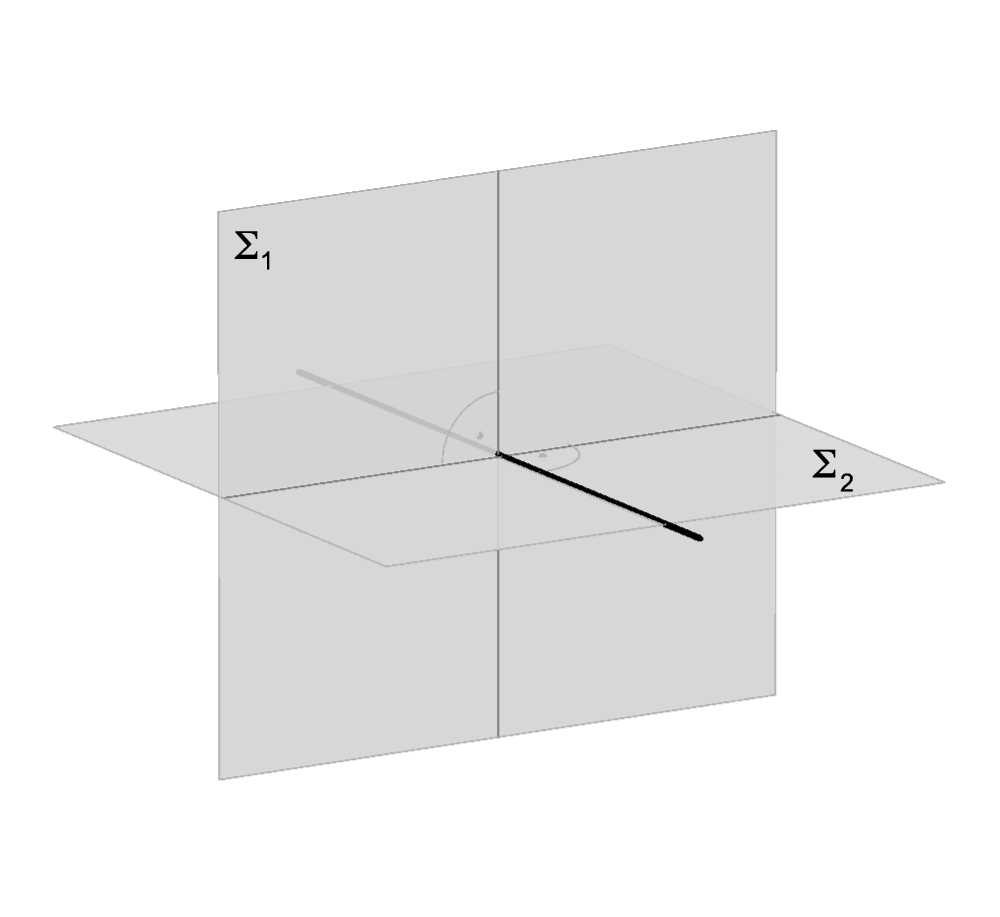Σ1 ⊥ Σ2 Σ2 ⊥ Σ1 Orthogonal projection Orthogonal projection Tp, of a point T to the line p, is the intersection of p and a line through T that is perpendicular to p and is contained in the plane determined by T and p. If the point T lies on the line p, then Tp=T. Orthogonal projection TΣ, of a point T to the plane Σ, is the intersection of the plane Σ and a normal line of Σ that passes through T. If the point T lies in Σ, then TΣ=T. Orthogonal projection pΣ, of a line p to the plane Σ, is a set of orthogonal projections of all points of the line p on the plane Σ. If the line p is a normal line of Σ, then its orthogonal projection is their intersecting point (TΣ = p ∩ Σ). In all other cases,  pΣ is a line. If the line p lies in the plane Σ, then pΣ=p. 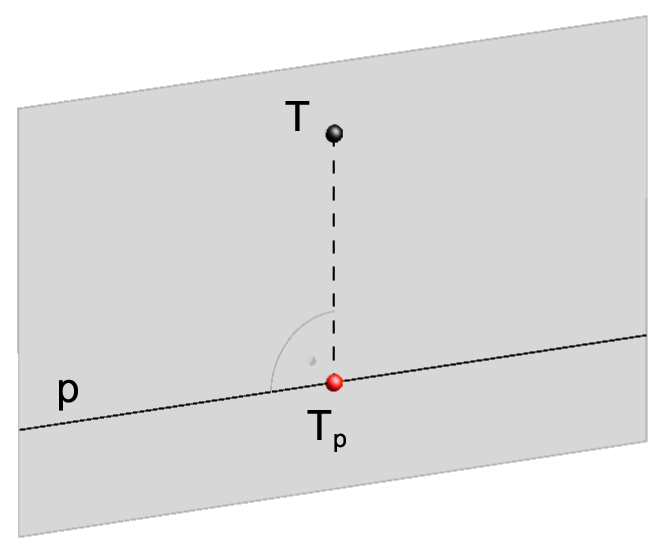Orthogonal projection of a point onto a line. 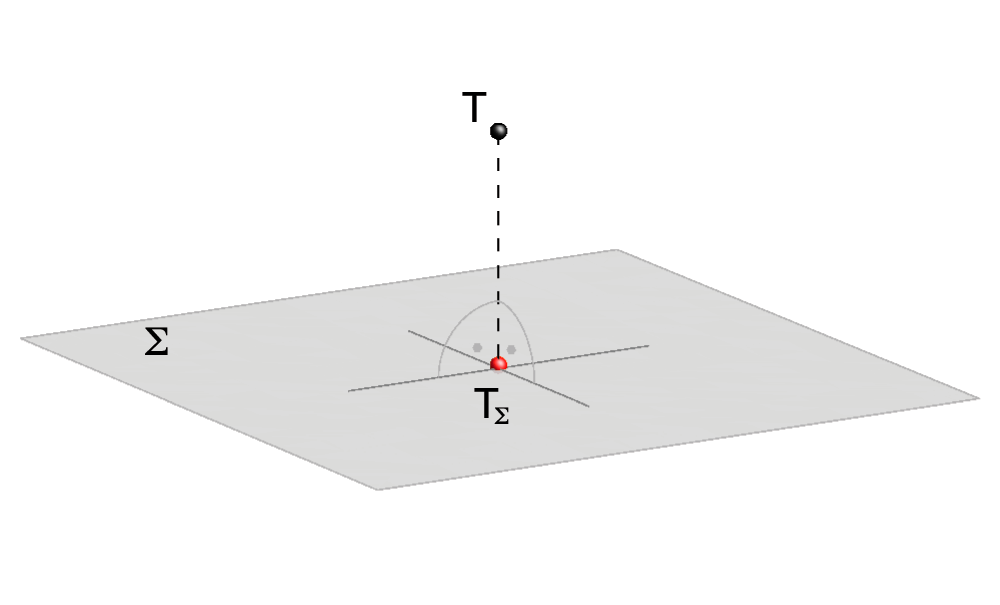Orthogonal projection of a point onto a plane. 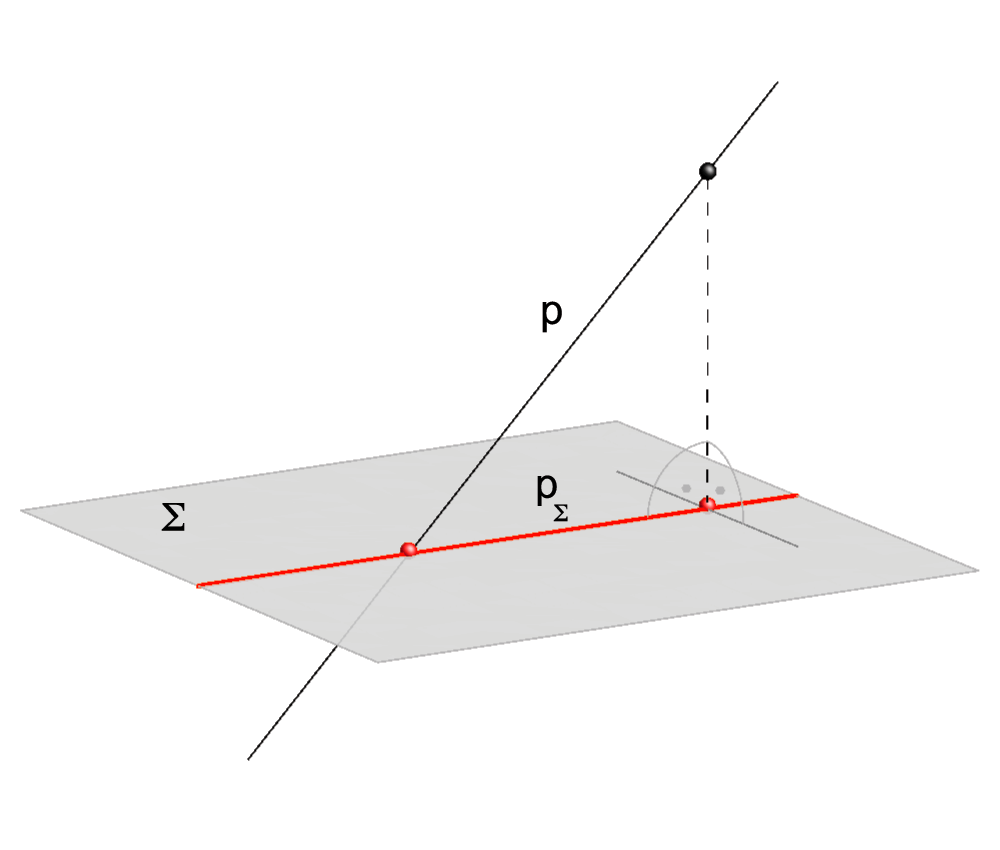Orthogonal projection of a line onto a plane. Angle between a line and a plane If a line is not perpendicular to a plane: The angle between the line and the plane equals the angle between the line and its orthogonal projection to the plane. If the line lies in the plane or is parallel to the plane, their angle equals 0o. If the line is perpendicular to the plane, their angle equals 90o. 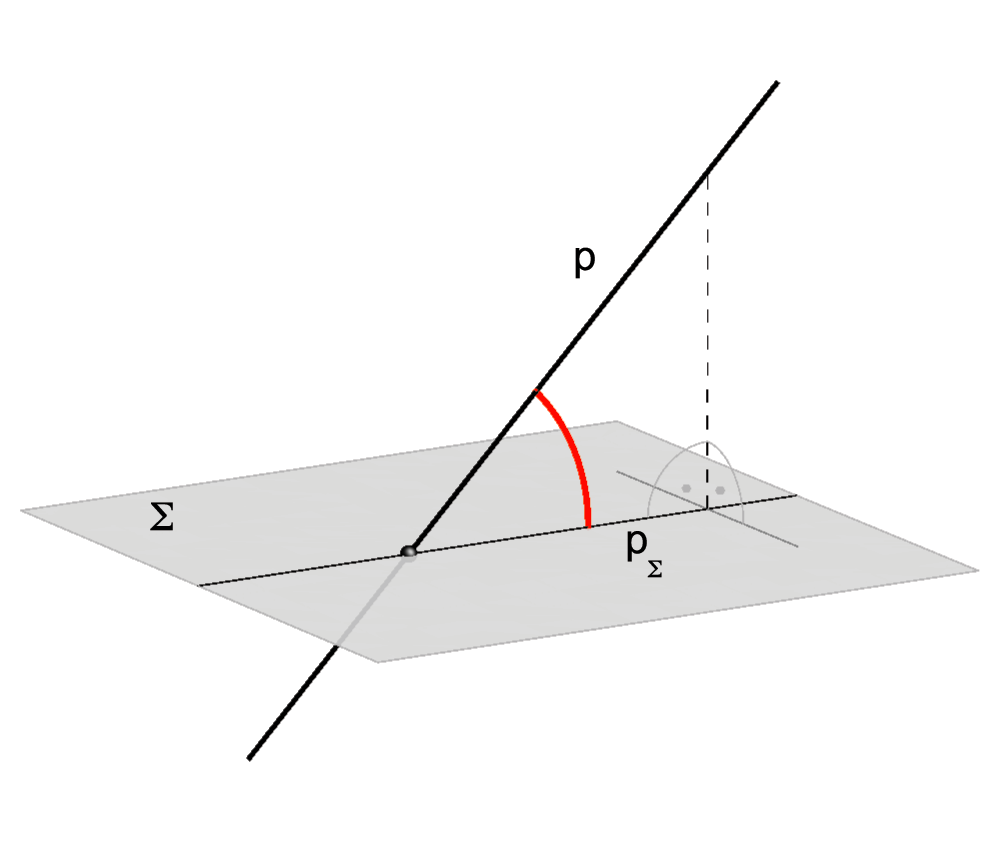Angle between the line and the plane. Angle between two planes Angle between two parallel planes equals 0o. We can define the angle between two planes in the following two ways:  Angle between two intersecting planes is the angle between any two lines, one line in each plane, that are perpendicular to the intersection line of the planes. Angle between two intersecting planes equals the angle between their normal lines. 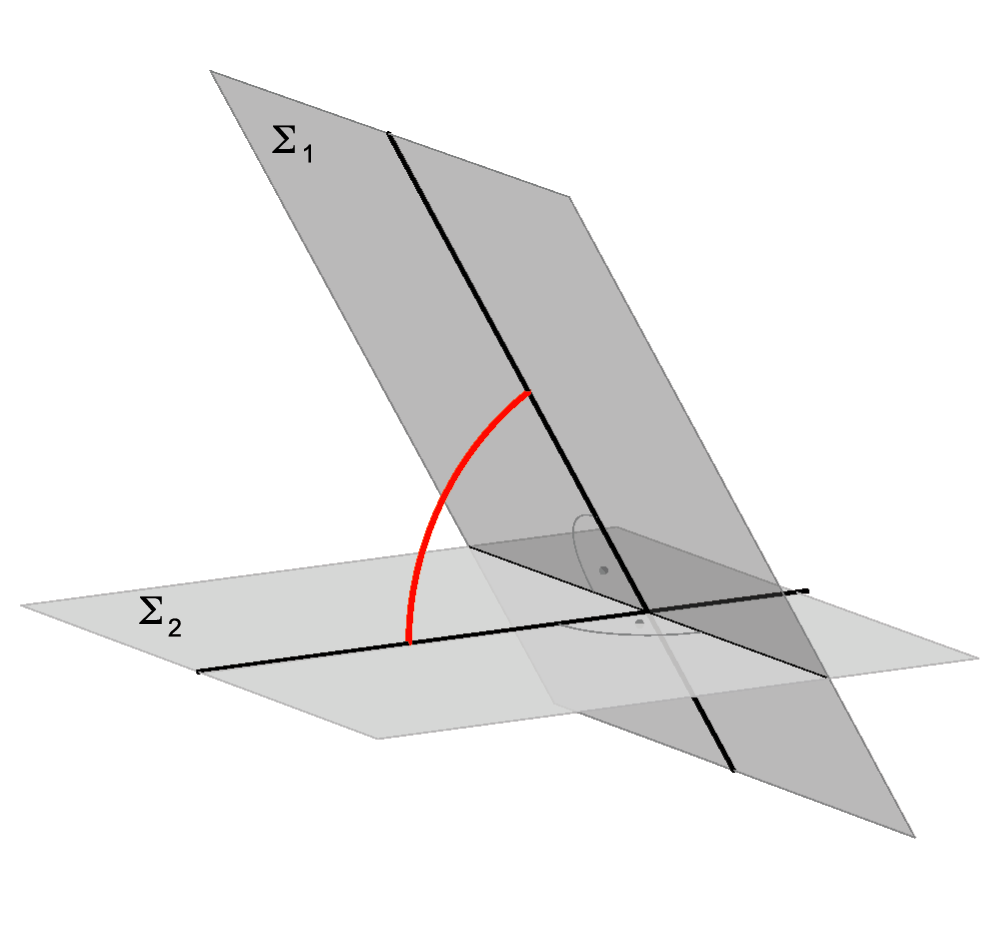Angle between two planes. 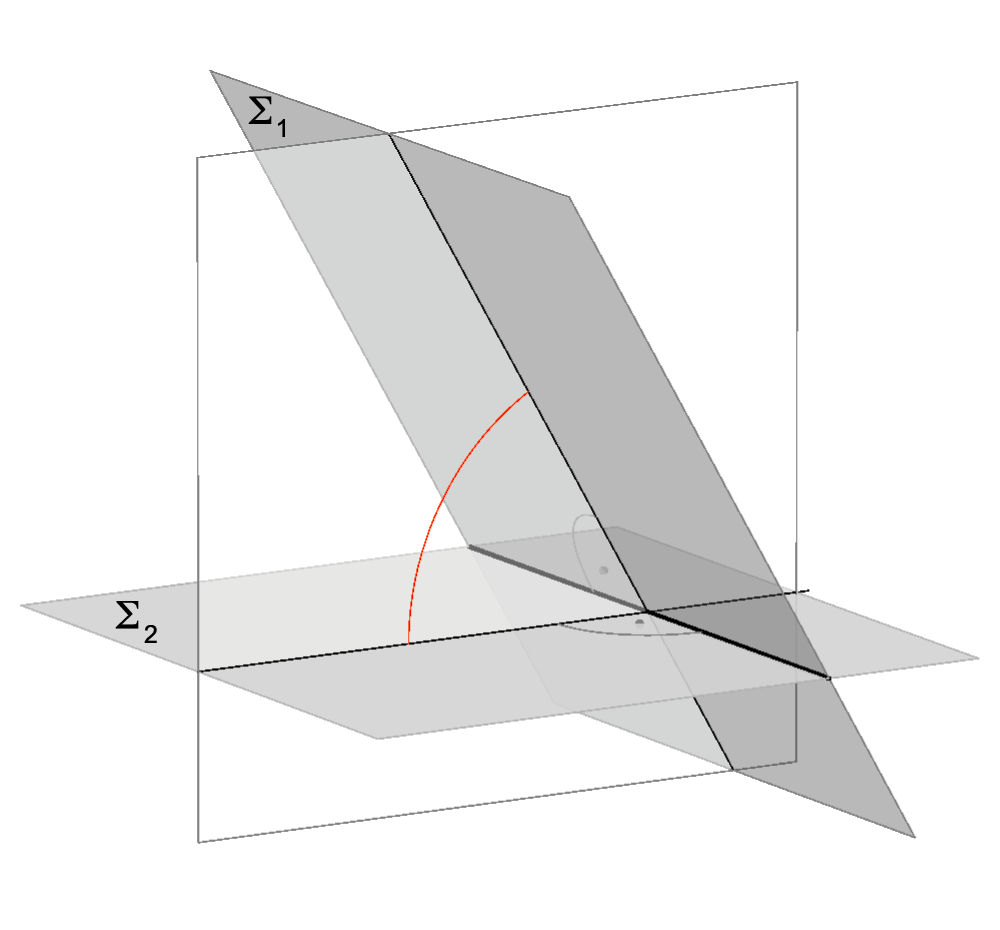Intersecting lines (used to measure the angle) lie in a plane perpendicular to the intersecting line of the planes. Distance Distance between two points The first measurement everyone learns is the distance between two points. The distance between points T1 and T2 equals the length of a line between T1 and T2. Number that denotes this length is d(T1,T2). If T1 = T2, then d(T1,T2) = 0. Distance between two sets of points Distance between two sets of points A and B equals to the smallest distance of points (one from each set). d(A,B) = min {d(A,B) | A ∈ A, B ∈ B}. Distance between a point and a line Distance between a point T and a line p equals the distance between the point T and its orthogonal projection to the line p, d(T,p) = d(T,Tp). Distance between a point and a plane Distance between a point T and a plane Σ equals the distance between the point T and its orthogonal projection to the plane Σ, d(T,Σ) = d(T,TΣ). Distance between two lines If the lines intersect, their distance equals 0. If the lines are parallel, their distance equals the distance between any point on one line and its orthogonal projection to the other line. Distance between two skew lines equals the distance between their intersections with their common normal line. For every pair of skew lines exists a unique line that intersects both lines and is perpendicular to both lines. This line is called normal line of two skew lines. 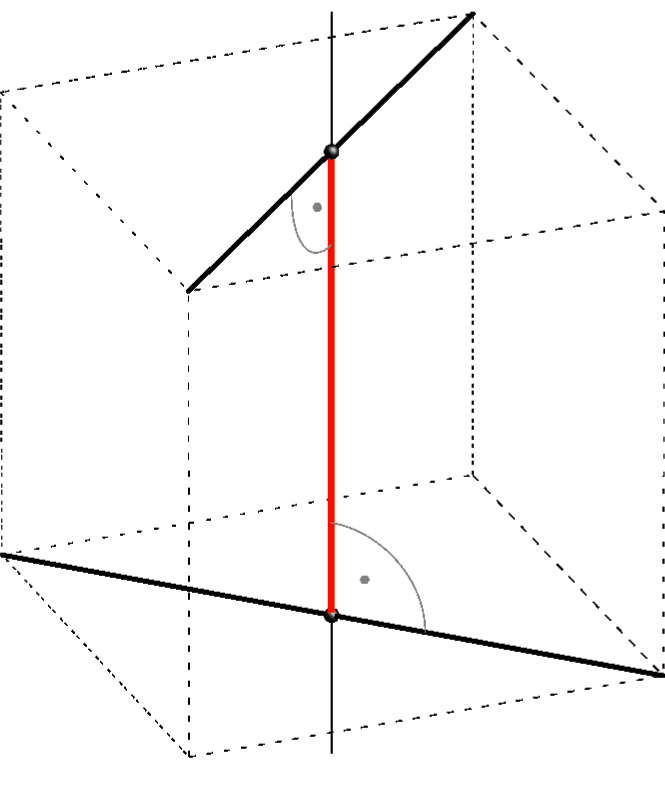Distance between two skew lines. Distance between a line and a plane If a line intersects a plane, their distance equals 0. If the line is parallel to the plane, their distance equals the distance of any point on the line and its orthogonal projection to the plane. Distance between two planes If two planes intersect, their distance equals 0. If two planes are parallel, their distance equals the distance of any point in one plane and its orthogonal projection to the other plane.

Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb