Extended Euclidean space In the previous chapter we studied extended Euclidean plane, whose basic elements are points and lines. Each line in the space is extended by a point at infinity, which is the common point of all lines parallel to the given line. All such points of the plane lie on one line- line at infinity. Every plane contains one line at infinity. In space there are three sets of basic elements: points, lines, and planes. Points at infinity and all the lines connecting them- lines at infinity of all the planes in the space, all lie in one plane called plane at infinity. Standard Euclidean space with added elements at infinity (points at infinity, lines at infinity and one plane at infinity that contains these points and lines) is called  extended Euclidean space. In this space the following holds: Each line has one point at infinity and this point is its intersection point with the plane at infinity. Any two parallel lines contain the same point at infinity and this point is their intersection. Each plane has one line at infinity and this line is the intersection line of that plane with the plane at infinity. Any two parallel planes contain the same line at infinity and this line is their intersection. If a line is parallel to a plane, then its point at infinity lies on the plane's line at infinity. The plane at infinity is parallel to all the lines and all the planes in the space. The axioms of three-dimensional projective space hold in extended Euclidean space. Most of them coincide with the axioms of standard Euclidean space, as an example: Three non-collinear points determine (are incident to) one and only one plane. One example of a statement that holds in the extended Euclidean space but fails in the standard: 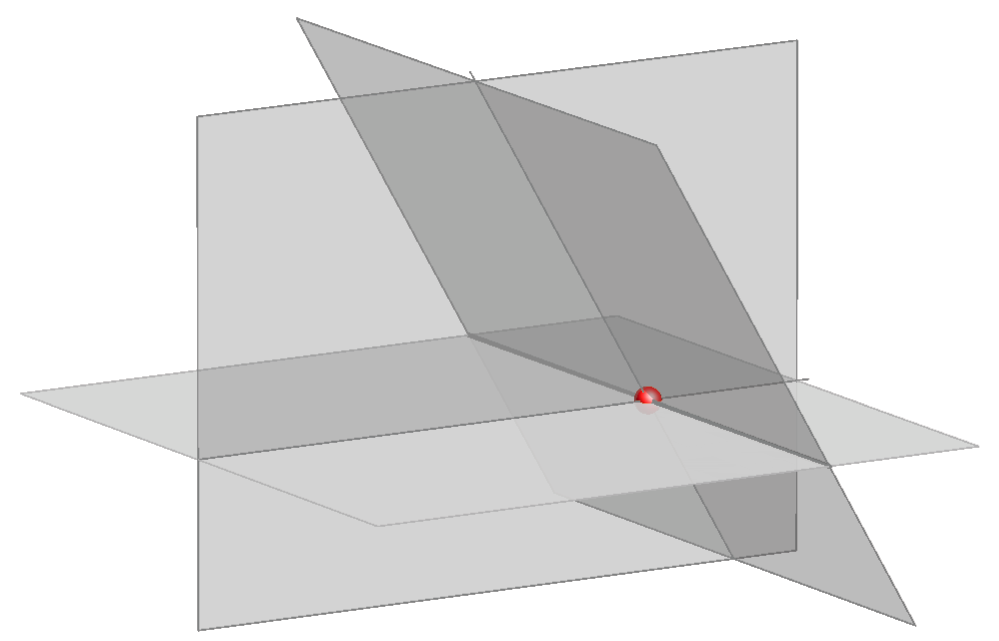Three non-collinear planes (these planes do not contain a same line) intersect at (are incident to) a unique point. Notice that each of these two statements can be derived from the other by replacing the words "point" and "plane", while the words "line" and "are incident" remain the same. This fact is the condition for the principle of duality that holds in the projective space - this principle asserts that every definition remains valid and every theorem remains true, when we interchange the words point and plane (an consequently also certain pairs of words such as lie in and intersect at). Therefore, if we prove a theorem in projective geometry, the dual theorem is also proved. Hence, dual elements of projective space are points and planes, while the lines are self-dual. Notions defined in a dual way are called dual notions. As an example of dual notions: range of points (p) - contains all points that lie on the line p, pencil of planes (p) - contains all planes that contain the line p.  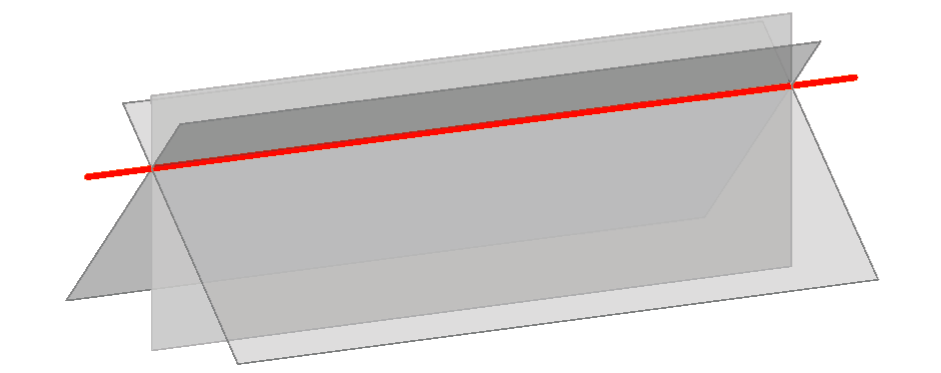 As it was already said about the projective plane: Projective geometry doesn't use measure (distance and angles). Measure is characteristic of Euclidean geometry and necessary in engineering. It will be very important to differentiate parallel lines and planes from intersecting lines and planes (distance between intersecting lines equals 0, which doesn't hold for parallel lines). Only once in a while, when the situation requires, we will expand the space we work in.

Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb