NORMALNA, GAUSSOVA I SREDNJA ZAKRIVLJENOST U REGULARNOJ TOČKI PLOHE

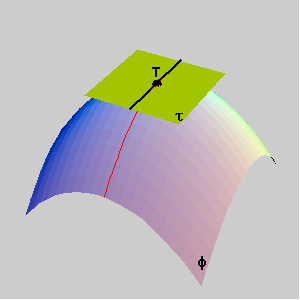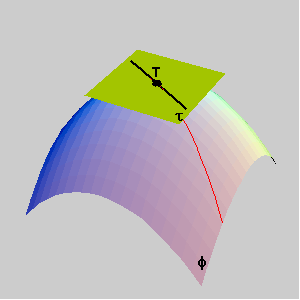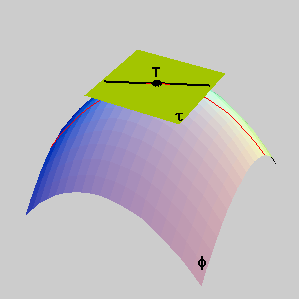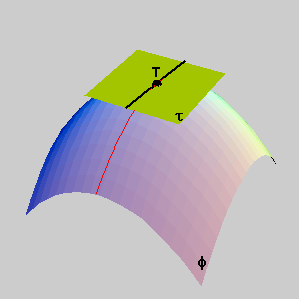
Gaussova i srednja zakrivljenost u regularnoj točki plohe važni su pojmovi diferencijalne geometrije. Za buduće je graditelje važno poznavanje ovih funkcija.

PRIMJER:
Krov od tkanine opterećen samo jednolikim silama prednapona poprima oblik opne od sapunice razapete na žicu savijenu u zadanu prostornu krivulju. Takva opna ima najmanju površinu od svih ploha koje zadovoljavaju iste rubne uvjete (koje se mogu razapeti na istu žicu) pa ju nazivamo minimalnom plohom. U svakoj točki takve plohe srednja je zakrivljenost jednaka nuli.

  • Pogledajte primjere visećih konstrukcija koji se nalaze na disku što su ga studenti našeg fakulteta Sanja Hak i Mario Uroš priložili svom radu "Gaussova i srednja zakrivljenost ploha - Mathematica vizualizacije", koji je ak. god. 2003/04 nagrađen Rektorovom nagradom.


    1. Regularne i singularne točke plohe

  • Točku T na plohi Φ nazivamo regularnom točkom plohe ako u njoj postoji jednistvena dirna (tangencijalna) ravnina plohe.

    PODSJETIMO SE!
    Za regularnu točku T tangencijalna ravnina t sadrži tangente s diralištem u T svih onih krivulja koje leže na plohi i prolaze točkom T. (Slika 1)

  • Točke u kojima takve tangente ne formiraju ravninu (formiraju više ravnina od kojih neke mogu biti i dvostruko brojene, ili algebarske stošce bilo kojeg reda n) nazivamo singularnim točkama plohe. (Slika 2)
    U takvim točkama funkcije Gaussove i srednje zakrivljenosti NISU definirane.

    • Slika 1

    Slika 2



    2. Normalna zakrivljenost, glavni i asimptotski smjerovi

    PODSJETIMO SE!
    U regularnoj točki ravninske krivulje apsolutna vrijednost zakrivljenosti k recipročna je polumjeru oskulacijske kružnice, dok joj predznak ovisi o orijentaciji normale. (Slika 3)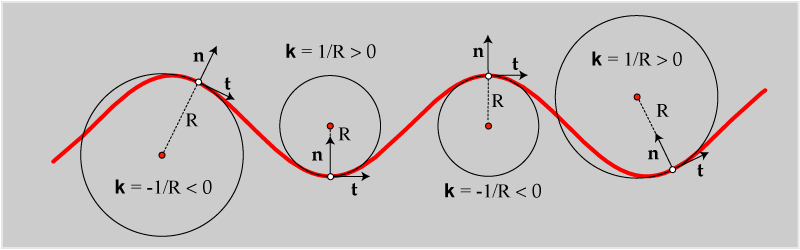

    Slika 3



  • Ravnine koje sadrže normalu n plohe Φ u točki T nazivamo ravninama normalnih presjeka kroz T.
    Svaka je takva ravnina određena normalom n i nekom od tangenata t plohe Φ u tangencijalnoj ravnini t .

  • U točki T zakrivljenost krivulje normalnog presjeka određenog tangentom t nazivamo normalnom zakrivljenošću plohe Φ u smjeru t u točki T i označavamo ju Kt.

  • Pomoću normalne zakrivljenosti Kt može se mjeriti zakrivljenost kt bilo koje druge krivulje na plohi Φ koja u T ima istu tangentu t. Vrijede relacije:

    Kt=kt cos θ, odnosno r = R cos θ. (Slika 4)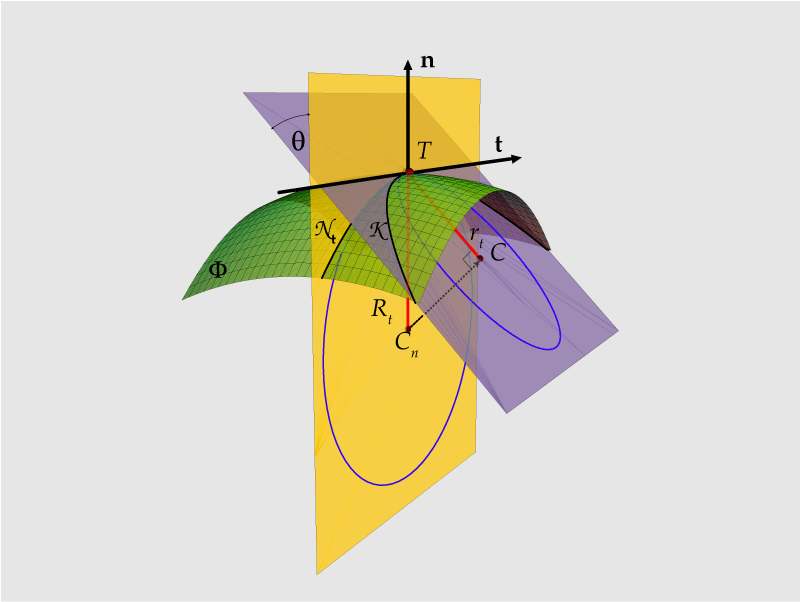

    • Slika 4



  • Promatramo normalne zakrivljenosti Kt u točki T.
  • Funkcija K (K(φ) = Kt) koja svakom smjeru tangente pridružuje zakrivljenost odgovarajućeg normalnog presjeka, na intervalu [0,π ] ima minimum i maksimum (K1 i K2).

    • Slika 5


  • Ekstremne zakrivljenosti K1 i K2 nazivamo glavnim zakrivljenostima plohe Φ u točki T.
  • Vektore tangenata pridruženih krivulja nazivamo glavnim smjerovima u T (označavat ćemo ih p1 i p2).
    Glavni su smjerovi uvijek ORTOGONALNI!
  • Ravnine određene normalom i glavnim smjerovima nazivamo glavnim ravninama.
  • Zakrivljenost Kt (K(φ) bilo kojeg normalnog presjeka može se izraziti pomoću glavnih zakrivljenosti K1 i K2.
    Vrijedi relacija:

    Kt=K1 cos2 φ+K2 sin2 φ,

    gdje je φ kut između tangente t i glavnog smjera p1. (Slika 6)


    Slika 6

  • Graf funkcije normalne zakrivljenosti može u odnosu prema osi j biti u položajima kao na slici 7.

    Slika 7

  • U ravninama normalnih presjeka kroz točku T mogu (ali ne moraju) postojati i krivulje kojima je zakrivljenost u točki T jednaka 0 (sučajevi b i c sa slike 7).

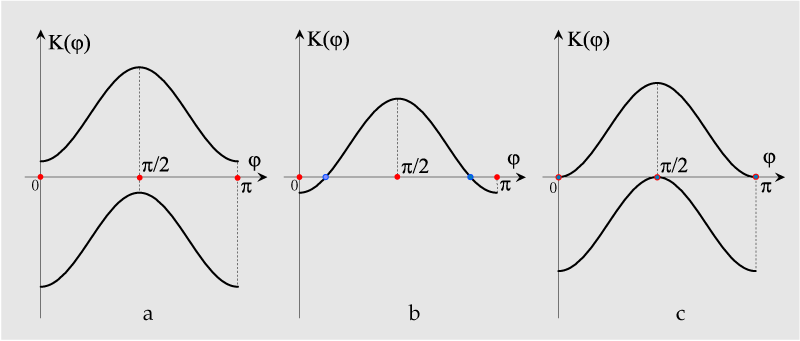
  • Vektore tangentata takvih krivulja nazivamo asimptotskim smjerovima plohe u točki T i označavamo ih a1 i a2.
    Oni odgovarju rješenjima kvadratne jednadžbe

    K1 cos2φ +K2 sin2 φ=0.

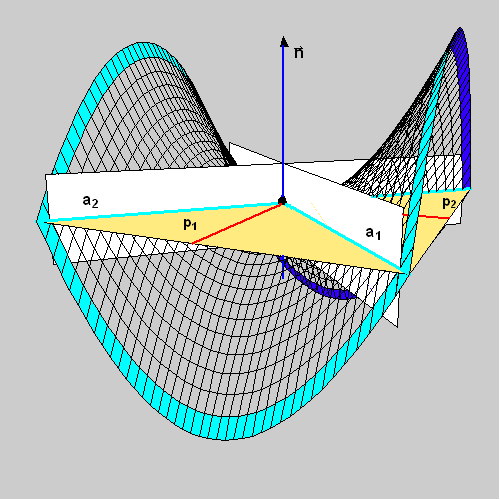
  • Ako u točki T postoje dva različita asimptotska smjera tada se glavni smjerovi podudaraju sa simetralama kutova između njih. (Slika 8)

    • Slika 8


    3. Gaussova i srednja zakrivljenost


    Gaussova (potpuna ili totalna) zakrivljenost plohe Φ u točki T jednaka je produktu odgovarajućih glavnih zakrivljenosti, tj.

    G(T) = K1(T) K2(T).



    Srednja zakrivljenost plohe Φ u točki T jednaka je polovini zbroja odgovarajućih glavnih zakrivljenosti, tj.

    H(T) = ½ (K1(T) + K2(T)).




    Ako nekoga zanima:
    slike_gauss.nb - Mathematica bilježnica s naredbama za crtanje slika i animacija koje se koriste u ovoj HTML datoteci.

    natrag