1. Normal, Gaussian and Mean Curvatures at the Regular Point of a Surface

The Gaussian and mean curvatures at the regular points of a surface are the terms of the differential geometry. For future structural engineers it is important to have knowledge of these functions.

EXAMPLE
Tensile fabric structure (e.g. membrane roof) in a uniform state of tensile prestress behaves like a soap film stretched over a wire which is bent in a shape of a closed space curve. Soap film assumes a form which has the minimal area relative to all other surfaces stretched over the same wire; this surface is therefore called minimal surface. It can be shown that mean curvature vanishes at each point of that surface.

  • See the examples of tensile structures which are on the CD which Sanja Hak and Mario Uroš, the students of our faculty, added to their paper "Gaussian and Mean Curvatures of Surfaces - - Mathematica Visualizations" which won the Rector's Prize in 2004.


    1.1 Regular and singular points of a surface

  • T is a regular point of a surface F if there exists the unique tangent plane t T.

    You have already learned that:
    The tangent plane t T at a regular point T contains all tangent lines of F at T. (Figure 1)

  • S is a singular point of a surface F if the tangent lines of F at S form two or more planes (some of them can be coincided) or the algebraic cones of any degree. (Figure 2)
    The Gaussian and mean curvatures are NOT defined at singular points.

    • Figure 1

    Figure 2



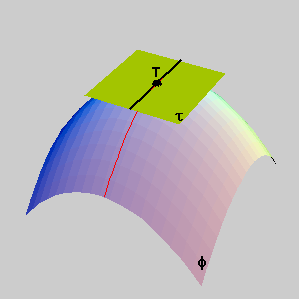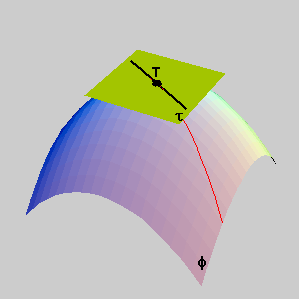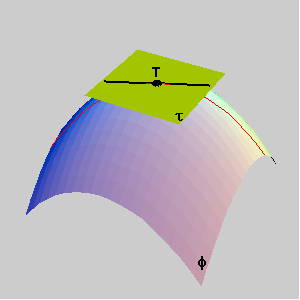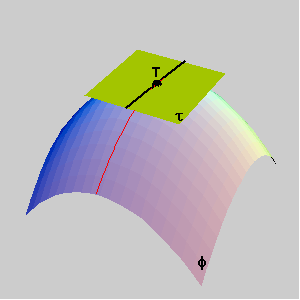
    1.2 Normal curvature, principal and asymptotic directions

    You have already learned that:
    The absolute value of the curvature k of a plane curve at its regular point T is equal to the curvature of its osculating circle. The sign of k depends on the orientation of the normal line at T. (Figure 3)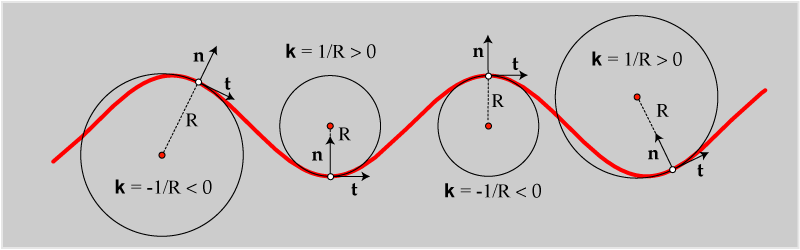

    Figure 3



  • Let t and n be the tangent and the normal line of a surface F at its regular point T. The plane through t and n cuts a surface F through the normal section at T in the direction t.

  • The normal curvature Kt of F at T in direction t is equal to the curvature of the corresponding normal section.

  • The curvatures of all other curves on F , which pass through T and have the same tangent t, are connected with Kt by the following formulas:

    Kt=kt cosq, or r = R cosq. (Meusnier's theorem - Figure 4)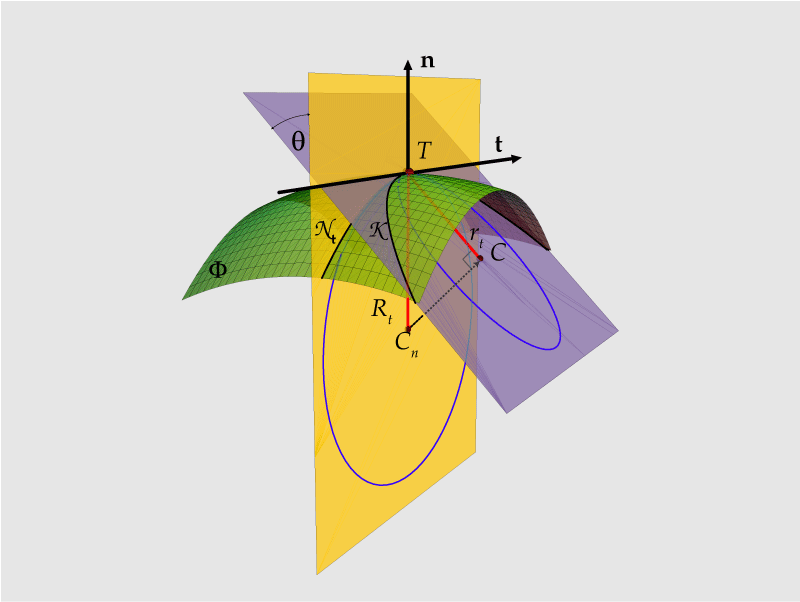

    • Figure 4



  • Let us observe now the normal curvatures Kt at T if the direction tangents t(j) pass through a tangent plane t . (Figure 5a)
  • The continuous function K : [0,p ]® R , K(j) = Kt(j) , has maximum and minimum on [0,p ]. (Figure 5b)

    • Figure 5a Figure 5b


  • Those extremal values K1 and K2 are the principal curvatures of surface F at point T.
  • The tangent lines p1 and p2, which determine the principal directions, are always orthogonal
  • The normal planes through p1 and p2 are the principal planes.
  • The normal curvature Kt is connected with K1 and K2 by the following formula

    Kt=K1 cos2 j+K2 sin2 j,

    where j is the angle between t and p1. (Figure 6)


    Figure 6

  • The graph of function Kt can be at different positions to axis j. (See Figure 7)

    Figure 7

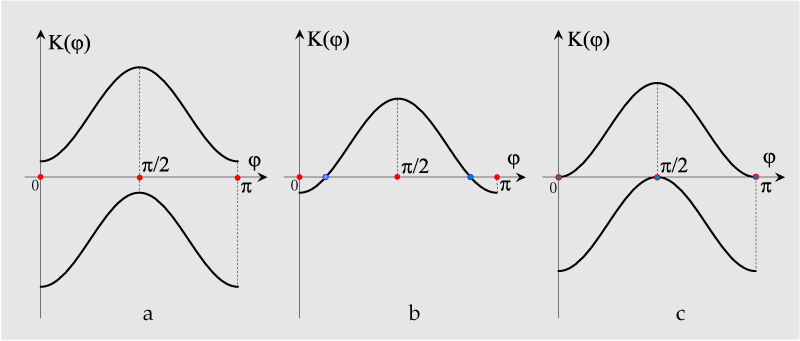
  • In the planes of normal sections through point T can (but not must) exist the curves with normal curvatures equal to 0 (cases b and c on figure 7).

  • The tangent vectors of these curves are the asymptotic directions of a surface at its point T and we denoted them a1 and a2.
    The asymptotic directions correspond to the roots of the quadratic equation

    K1 cos2j +K2 sin2 j=0.

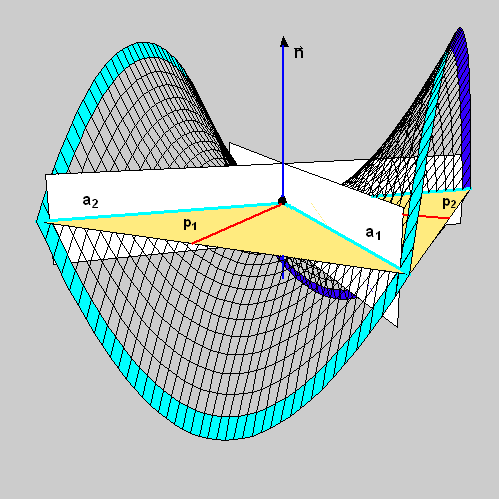
  • If two different asymptotic directions exist at point T, then principal directions bisect the angle between them. (Figure 8)

    • Figure 8


    1.3 Gaussian and mean curvatures


    The Gaussian curvature G of a surface F at its regular point T is related to the principal curvatures in T by the formula:

    G(T) = K1(T) K2(T).



    The mean curvature H of a surface F at its regular point T is related to the principal curvatures in T by the formula:

    H(T) = ½ (K1(T) + K2(T)).




    If you are inerested in Mathematica notebook containing inputs for drawing pictures and animations used in this file download slike_gauss.nb.

    back