3.1 The Hyperbolic Paraboloid

Revise the properties of the hyperbolic paraboloid! (HYPAR - in Croatian)

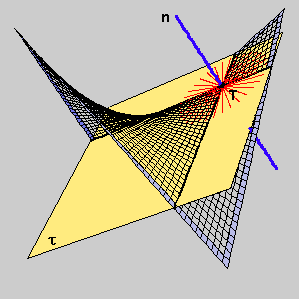
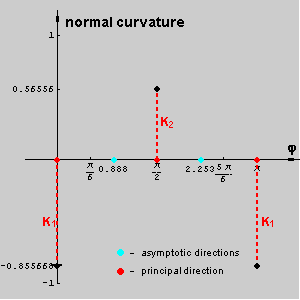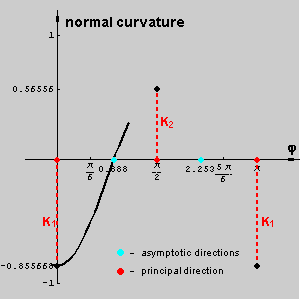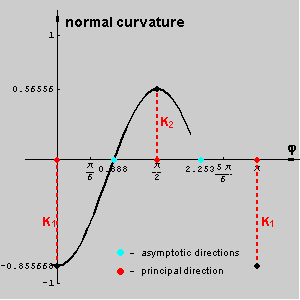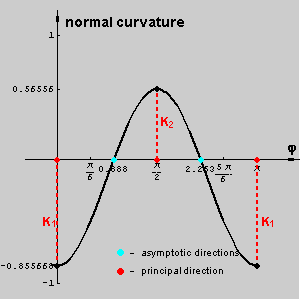
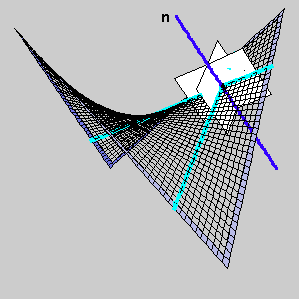
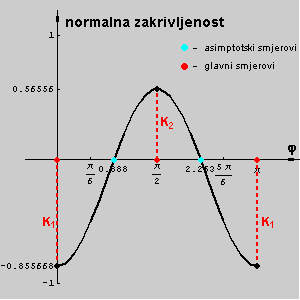
3.1.1 Normal curvatures, asymptotic and principal directions

All points of the hyperbolic paraboloid (hypar) are regular. The tangent plane at T cuts a hypar into the pair of rulings. (Hypar is a double ruled surface). The normal line n through T is perpendicular to the tangent plane t T. The pencil of lines (T) in the plane t T contains the tangent lines to all curves on a hypar which pass through a point T.

We observe the pencil of planes [n] and the curvatures of the normal sections in those planes. The normal curvature of a hypar at a point T is a function which has maximum and minimum at the segment [0,p]. The angles for those extremal values correspond to the principal directions, and the angels where normal curvature is zero correspond to the asymptotic directions.

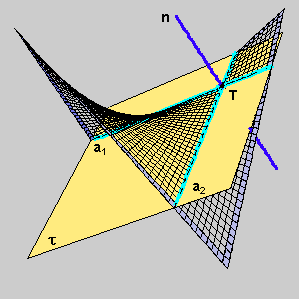
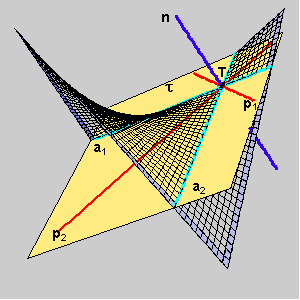
The asymptotic directions at a point T lying on a hypar are defined with two rulings through T.

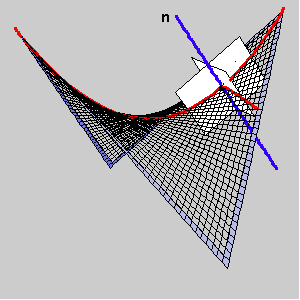
The principal directions at a point T lying on a hypar bisect the angle between the asymptotic direction.

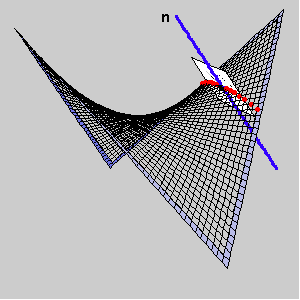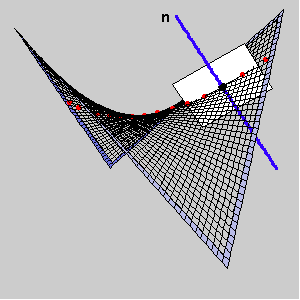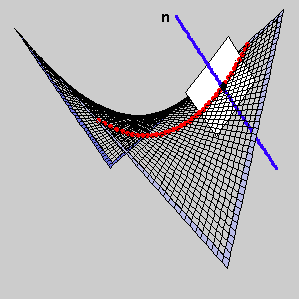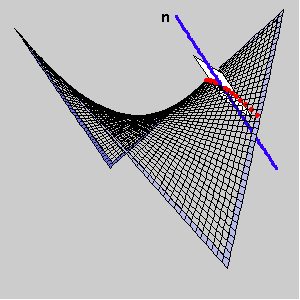
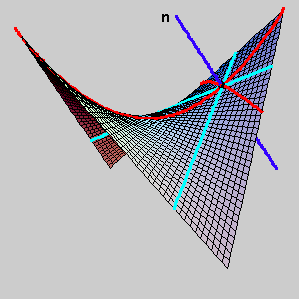
The following pictures show the normal sections through the principal and asymptotic directions and a graph of hyper normal curvature at T.

3.1.2 Mathematica visualisations of Gaussian and mean curvatures

For the following visualisations we used the periodical Mathematica color function Hue (period 1). It is defined in the following way:

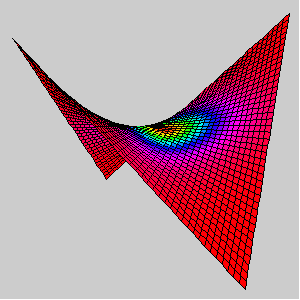A hypar coloured by Hue[G]. 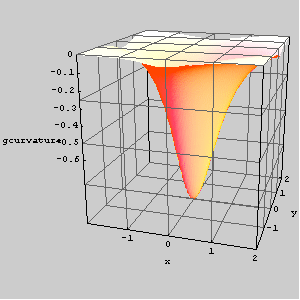The graph of the Gaussian curvature of a hypar.



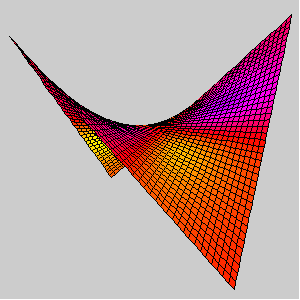A hypar coloured by Hue[H]. 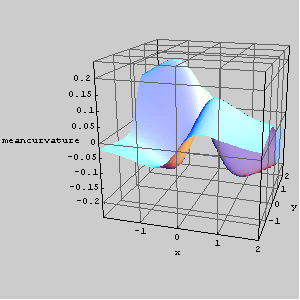The graph of the mean curvature of a hypar.


If you are inerested in Mathematica notebook containing inputs for drawing pictures and animations used in this file download slike_hipar.nb.
back