OPĆENITO O PRAVČASTIM PLOHAMA
Jednoparametarski skup neprekinuto povezanih pravaca prostora nazivamo pravčastom plohom.
Pravce toga skupa nazivamo izvodnicama pravčaste plohe.
Ako se svake dvije neizmjerno blize izvodnice plohe sijeku, plohu nazivamo razvojnom pravčastom plohom.
Takve je plohe moguće razviti u ravninu.
U razvojne pravčaste plohe spadaju stošci i valjci bilo kojeg reda te plohe što ih čine tangente prostornih krivulja.
Ako su svake dvije neizmjerno blize izvodnice plohe mimosmjerne plohu, nazivamo vitoperom pravčastom plohom.
Takve se plohe ne mogu razmotati u ravninu.
U ovom ćemo poglavlju obrađivati samo vitopere pravčaste plohe.
1. Izvođenje
|
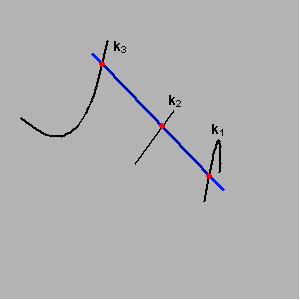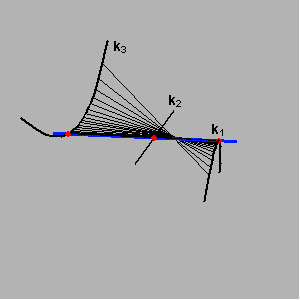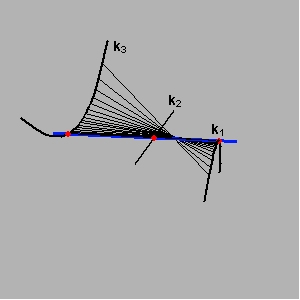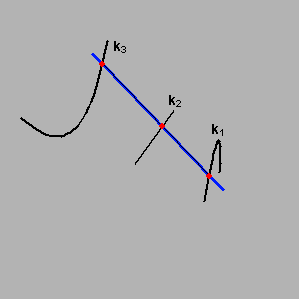
Postoji više načina konstruktivnog izvođenja pravčastih ploha. Jedan od njih (koji koristimo u okviru našeg kolegija) je taj da su pravčaste plohe sistemi pravaca koji sijeku tri prostorne krivulje
k1, k2 i k3.
Prostorne krivulje k1, k2 i k3 nazivamo ravnalicama, a pravce koji ih sijeku izvodnicama pravčaste plohe.
|
|
2. Konoidi
|
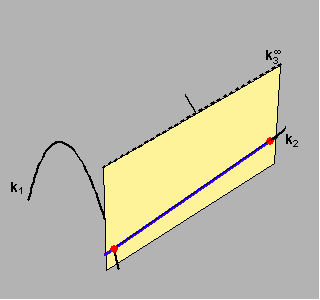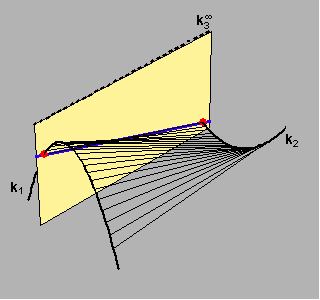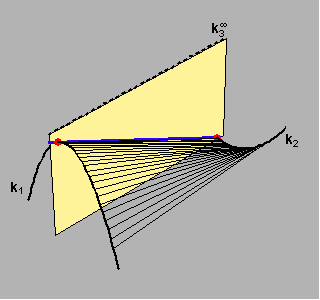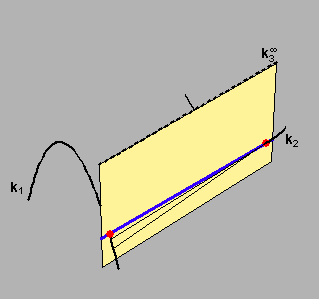
Pravčaste plohe kojima je jedna ravnalica beskonačno daleki pravac nazivamo konoidima.
Ravnine koje sadrže takvu beskonačno daleku ravnalicu nazivamo direkcijskim ravninama pravčaste plohe.
|
|
3. Stupanj algebarske pravčaste plohe
Ako se kao ravnalice odaberu algebarske krivulje (koje su karakterizirane redom i razredom) nastaje
algebarska pravčasta ploha.
Red i razred takve pravčaste plohe uvijek se podudaraju, tj. algebarske pravčaste plohe imaju stupanj.
Za izračunavanje stupnja pravčaste plohe koristimo sljedeće teoreme.
Teorem 1
Ako ravnalice k1, k2 i k3, redova n1, n2 i n3, nemaju zajedničkih točaka, tada je red pravčaste plohe 2n1n2n3
Međutim, ako se primjerice ravnalice k1 i k2 sijeku u jednoj točki tada svi pravci koji prolaze tom točkom,
a sijeku krivulju k3 pripadaju plohi i formiraju stožac reda n3.
Pravčasta se ploha raspada na stožac reda n3 i ostatak koji je reda 2n1n2n3 - n3.
Upravo je taj ostatak ono što smatramo izvedenom pravčastom plohom i što konstruktivno obrađujemo.
Na sljedećim su slikama (za slučajeve n3=2,1) prikazani stošci koje izuzimamo prilikom računanja reda pravčaste plohe.
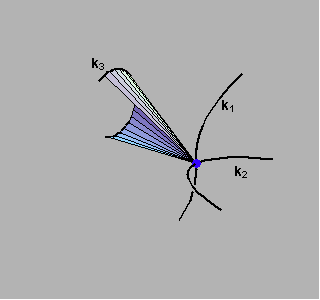
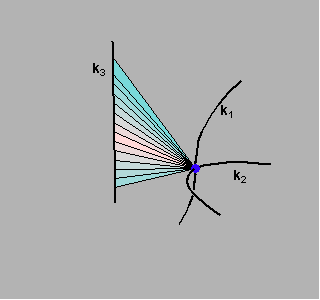
Za opći slučaj vrijedi sljedeći teorem.
Teorem 2
Ako se krivulje k1 i k2 sijeku u s3, krivulje k1 i k3 u s2, a krivulje k2 i k3 u s1 točaka tada je red pravčaste plohe jednak 2n1n2n3 - (n1s1 + n2s2 + n3s3).
4. Višestruke linije pravčastih ploha
Višestrukom (dvostrukom, trostrukom, n-strukom) linijom pravčaste plohe nazivamo onu krivulju na plohi za koju vrijedi da svakom njezinom točkom prolazi više (2, 3, n) izvodnica plohe.
|
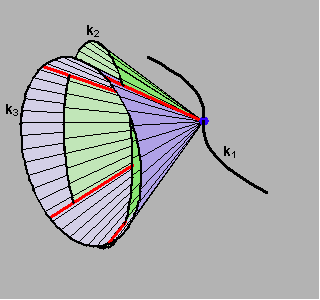
Izvodnice plohe koje prolaze primjerice nekom točkom ravnalice k1 zajedničke su izvodnice dvaju stožaca određenih vrhom u toj točki te ravnalicama k2 i k3.
Takva dva stošca sa zajedničkim vrhom sijeku se u raspadnutoj krivulji reda n2n3 tj. u n2n3 pravaca.
Na slici je prikazan slučaj n2 = n3 = 2.
|
|
Ako se ravnalice sijeku neke od izvodnica pripadati će onom dijelu raspada plohe koji izuzimamo, pa za opći slučaj vrijedi sljedeći teorem.
Teorem 3
Višestruke linije algebarske pravčaste plohe su njezine ravnalice k1, k2 i k3 sa stupnjevima višestrukosti
n2n3 - s1, n1n3 - s2 i n1n2 - s3.
5. Dirne ravnine pravčastih ploha
Za dirne ravnine pravčastih ploha vrijede sljedeći teoremi.
Teorem 4
Dirna ravnina, s diralištem na izvodnici i algebarske pravčaste plohe stupnja n, siječe tu plohu po izvodnici i i krivulji reda n-1.
Sljedeća slika prikazuje jedan konoid 4. reda, jednu njegovu izvodnicu, nekoliko dirnih ravnina plohe s diralištima na toj izvodnici i krivulje 3. reda u kojima te dirne ravnine sijeku konoid.
Uočite da se u dirnoj ravnini koja ima diralište na dvostrukom pravcu plohe presječna krivulja 3. reda raspada na taj dvostuki pravac plohe i još jednu izvodnicu.

Teorem 5
Za svaku izvodnicu i pravčaste plohe vrijedi da su pramen dirnih ravnina [i] i niz njima pridruženih dirališta (i) u projektivnom odnosu.
Na sljedećoj je slici prikazan konoid 4. reda, jedna njegova izvodnica i tri dirne ravnine s diralištima na toj izvodnici.
Tri para pridruženih elemenata jednoznačno određuju projektivno pridruženje.
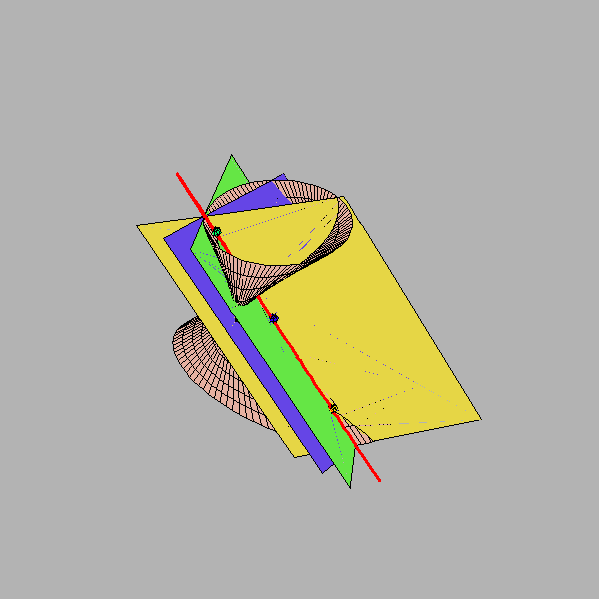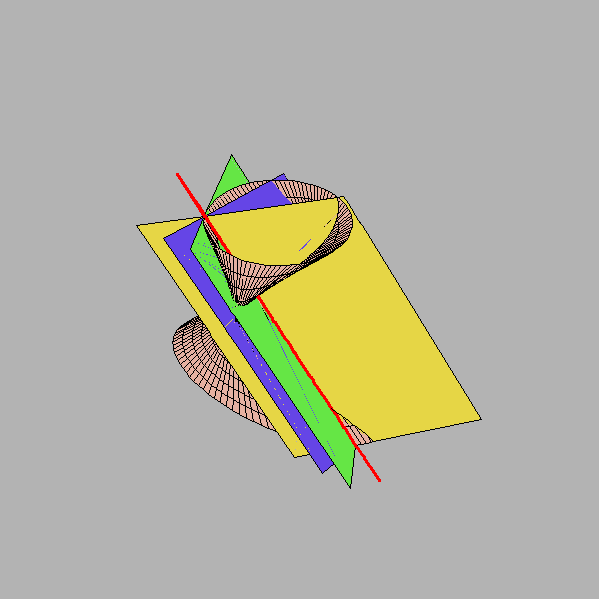
6. Sistemi izvodnica pravčastih ploha
Za sve pravčaste plohe stupnja većeg od 2 vrijedi da imaju samo jedan sistem izvodnica, tj. svakom točkom takve plohe koja ne leži na višestrukoj liniji prolazi samo jedna izvodnica.
Samo na vitoperim pravčastim plohama 2. stupnja (paraboličkom i jednokrilnom hiperboloidu) postoje dva sitema izvodnica, tj. svakom točkom takve plohe prolaze dvije izvodnice, po jedna iz svakog sistema.
Sve izvodnice jednog sistema međusobno su mimosmjerne, dok svaka od njih siječe sve izvodnice drugog sistema.
 natrag
natrag






