Primjer 1.

Za nosač sa slike analitičkim postupkom odrediti dijagrame momenata, te poprečnih i uzdužnih sila, ako je zadano | $\vec{{K}}$ | = 90 kN i tg $\alpha$ = ${\frac{{4}}{{3}}}$ .

$\includegraphics[scale=1.15]{z1sl/grp1.1}$

Prvo treba odrediti reakcije u ležajevima; reakciju u ležaju A označit ćemo sa $\vec{{A}}$ , a u B sa $\vec{{B}}$ . Silu $\vec{{A}}$ možemo prikazati kao (vektorski) zbroj horizontalne i vertikalne komponente,

$\displaystyle \vec{{A}}$ = $\displaystyle \vec{{A}}^{h}_{}$ + $\displaystyle \vec{{A}}^{v}_{}$ = A^h $\displaystyle \vec{{\imath}}$ + A^v $\displaystyle \vec{{\jmath}}$ ,

dok je reakcija $\vec{{B}}$ vertikalna, $\vec{{B}}$ = $\vec{{B}}^{v}_{}$ .

$\includegraphics[scale=1]{z1sl/grp1.2}$

Komponente sile $\vec{{K}}$ su

K^v = | $\displaystyle \vec{{K}}$ | sin $\displaystyle \alpha$ = 72 [kN], K^h = | $\displaystyle \vec{{K}}$ | cos ( $\displaystyle \pi$ - $\displaystyle \alpha$ ) = - | $\displaystyle \vec{{K}}$ | cos $\displaystyle \alpha$ = - 54 [kN],

pa je

$\displaystyle \vec{{K}}$ = K^h $\displaystyle \vec{{\imath}}$ + K^v $\displaystyle \vec{{\jmath}}$ = - 54 $\displaystyle \vec{{\imath}}$ + 72 $\displaystyle \vec{{\jmath}}$ .

Uvjeti ravnoteže, izraženi vektorski, su:

	$\displaystyle \vec{{A}}$ + $\displaystyle \vec{{B}}$ + $\displaystyle \vec{{K}}$ = $\displaystyle \vec{{0}}$ ,
	$\displaystyle \vec{{r}}_{{A}}^{}$ × $\displaystyle \vec{{A}}$ + $\displaystyle \vec{{r}}_{B}^{}$ × $\displaystyle \vec{{B}}$ + $\displaystyle \vec{{r}}_{C}^{}$ × $\displaystyle \vec{{K}}$ = $\displaystyle \vec{{0}}$ ,

gdje su $\vec{{r}}_{{A}}^{}$ , $\vec{{r}}_{{B}}^{}$ i $\vec{{r}}_{{C}}^{}$ radijus vektori točaka A, B i C u odnosu na po volji odabranu točku redukcije.

Prvi uvjet, kojega možemo razviti u izraz

(A^h + K^h) $\displaystyle \vec{{\imath}}$ + (A^v + B^v + K^v) $\displaystyle \vec{{\jmath}}$ = 0,

daje prve dvije jednadžbe ravnoteže:

	A^h + K^h = 0,
	A^v + B^v + K^v = 0,

ili, ostavimo li slijeva samo nepoznanice:

	A^h = - K^h,
	A^v + B^v = - K^v.

Drugi uvjet, prikažemo li vektorski produkt pomoću determinante, glasi

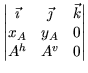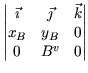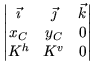$\displaystyle \begin{vmatrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ x_{A} & y_{A} & 0 \\ A^h & A^v & 0 \end{vmatrix}$ + $\displaystyle \begin{vmatrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ x_{B} & y_{B} & 0 \\ 0 & B^v & 0 \end{vmatrix}$ + $\displaystyle \begin{vmatrix} \vec{\imath} & \vec{\jmath} & \vec{k} \\ x_{C} & y_{C} & 0 \\ K^h & K^v & 0 \end{vmatrix}$ = $\displaystyle \vec{{0}}$ ,

odnosno, razvijemo li determinante,

(A^{v .}x_A - A^{h .}y_A) $\displaystyle \vec{{k}}$ + (B^{v .}x_B) $\displaystyle \vec{{k}}$ + (K^{v .}x_C - K^{h .}y_C) $\displaystyle \vec{{k}}$ = $\displaystyle \vec{{0}}$ ,

pa je treća jednadžba ravnoteže, nakon prebacivanja poznatoga na desnu stranu:

A^{v .}x_A - A^{h .}y_A + B^{v .}x_B = - K^{v .}x_C + K^{h .}y_C.

Dobili smo, prema tome, tri jednadžbe:

	A^h = - K^h,
	A^v + B^v = - K^v,
	A^{v .}x_A - A^{h .}y_A + B^{v .}x_B = - K^{v .}x_C + K^{h .}y_C,

s nepoznanicama A^h, A^v, B^v. Prva jednadžba neposredno daje A^h = - K^h = - (- 54) = 54 [kN]. (Sila $\vec{{A}}^{h}_{}$ djeluje u pozitivnom smjeru osi x.) Uvrštavanjem dobivene vrijednosti u treću jednadžbu (i sređivanja) nastaje sustav od dvije jednadžbe s dvije nepoznanice A^v i B^v.

No, odaberemo li za točku redukcije točku A, iz jednadžbe

A^{v .}x_A - A^{h .}y_A + B^{v .}x_B = - K^{v .}x_C + K^{h .}y_C

ispadaju i A^h i A^v, pa ta jednadžba neposredno daje

B^v = - $\displaystyle {\frac{{x_C}}{{x_B}}}$ ^.K^v + $\displaystyle {\frac{{y_C}}{{x_B}}}$ ^.K^h = - $\displaystyle {\tfrac{{4}}{{6}}}$ ^.72 + $\displaystyle {\tfrac{{3}}{{6}}}$ ^.(- 54) = - 75 [kN];

iz negativne vrijednosti zaključujemo da sila $\vec{{B}}^{v}_{}$ djeluje odozgo prema dolje.

Uz poznatu vrijednost B^v iz preostale jednadžbe izračunavamo na kraju i

A^v = - K^v - B^v = - 72 - (- 75) = 3 [kN];

$\vec{{A}}^{v}_{}$ djeluje, dakle, prema gore.

Kako se u točki C os nosača `lomi', izraze za unutarnje sile izvest ćemo posebno za dio A- C, a posebno za dio C- B.

U po volji odabranoj točki dijela A- C `presijecamo' nosač te postavljamo jednadžbe ravnoteže za lijevi dio nosača (dio od točke A do zamišljenog presjeka). Na taj dio, osim reakcija (i, u općenitijem slučaju, zadanih sila), djeluju i sile u presjeku. (Na crtežu smo naznačili dogovorne pozitivne smjerove unutarnjih sila, s kojima te sile ulaze u jednadžbe ravnoteže. Ishodište lokalnog koordinatnog sustava je u točki A.)

$\includegraphics[scale=1]{z1sl/grp1.3}$

Izraz za moment savijanja dobivamo iz jednadžbe ravnoteže momenata oko težišta odabranog presjeka:

M_x = A^{v .}x - A^{h .}x^.tg $\displaystyle \beta$ = A^{v .}x - A^{h .}(3/4) x = - 37, 5 x,

gdje je x = x_glob.

Napišemo li jednadžbe ravnoteže projekcija sila na horizontalnu i vertikalnu os, u obje će se jednadžbe kao nepoznanice pojaviti i poprečna i uzdužna sila. Pogodnije je stoga postaviti uvjete ravnoteže sila u smjeru osi promatranog dijela nosača, te sila okomito na tu os, drugim riječima, u lokalnom koordinatnom sustavu; ti izrazi neposredno daju:

T_x	= - A^vcos $\displaystyle \beta$ + A^hsin $\displaystyle \beta$ = 30 kN,
N_x	= - A^vsin $\displaystyle \beta$ - A^hcos $\displaystyle \beta$ = - 45 kN.

Na analogan ćemo način izvesti izraze za dio C- B. Pišemo jednadžbe ravnoteže za dio nosača od ležaja B do po volji odabranog presjeka između točaka C i B. (Dogovorni pozitivni smjerovi unutarnjih sila prikazani su na crtežu. Ishodište lokalnog koordinatnog sustava je u točki B.)

$\includegraphics[scale=1]{z1sl/grp1.4}$

Izrazi za unutarnje sile za dio C- B glase:

M_x = - B^{v .}x = 75x, T_x = B^v = - 75 kN, N_x = 0 kN;

sada je x = x_lok.

Grafički su prikaz izvedenih izraza dijagrami unutarnjih sila:

$\includegraphics[scale=1]{z1sl/grp1.5}$

KF 2001-12-09