U metodi Runge-Kutta se također računa ![]() pomoću već
poznate vrijednosti
pomoću već
poznate vrijednosti ![]() Taj račun je točniji, jer
uzima u obzir i neke međuvrijednosti funkcije
Taj račun je točniji, jer
uzima u obzir i neke međuvrijednosti funkcije ![]() Imamo
sljedeći algoritam
Imamo
sljedeći algoritam
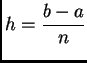
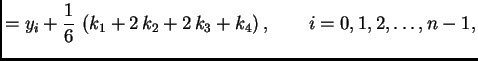 |
||
|
gdje je
| ||
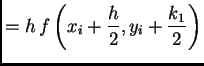 |
||
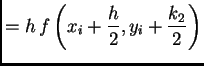 |
||
Radi bolje preglednosti prilikom računanja se može koristiti sljedeća tabela.
| 0 | ||||
|
|
|
|||
|
|
|
|||
|
|
||||
|
|
|
|||
|
|
|
|||
|
|
||||
| ... | ... | ... | ... |
f[x_,y_]=; (* zadavanje f(x,y), ako je y'=f(x,y) *)
x=;y=; (* po\1etni uvjet *)
h=; (* korak *)
rj={{x,y}};
br=0; (* po\1etna vrijednost broja\1a *)
n=; (* broj koraka *)
While[br<n,
k1=h f[x,y];
k2=h f[x+h/2,y+k1/2];
k3=h f[x+h/2,y+k2/2];
k4=h f[x+h,y+k3];
br=br+1;
x=x+h;
y=y+(k1+2 k2+2 k3+k4)/6;
rj=Append[rj,{x,y}]];
N[rj,10] (* ispis rezultata s deset znamenaka *)
Rješenje. Primijenimo li gornji program, koji slijedi algoritam metode Runge-Kutta, dobivamo sljedeće točke grafa rješenja.
| 0 | ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Postoji cijela familija metoda zasnovanih na ideji da se podsegment podijeli na još manje dijelove kako bi se izračunala vrijednost u sljedećem čvoru. Sve one nose naziv Runge-Kutta metode. Opisani postupak se najčešće upotrebljava.