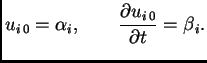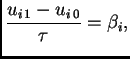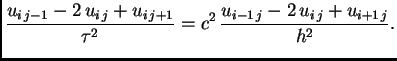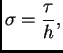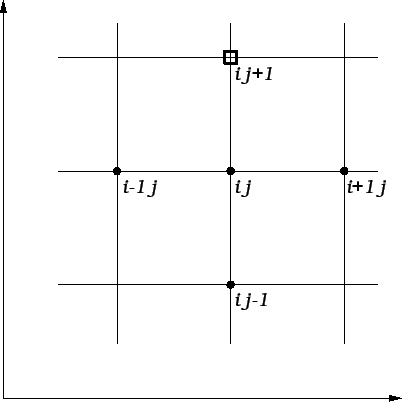Next: Varijacijske metode
Up: Metoda konačnih diferencija
Previous: Jednadžba provođenja
Sadržaj
Indeks
Valna jednadžba
Problem koji sada rješavamo je
Diskretizaciju područja učinimo kao kod jednadžbe
provođenja. Razlika je u tome što u jednadžbi dolazi druga
parcijalna derivacija po 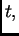 i što imamo dodatni početni
uvjet.
i što imamo dodatni početni
uvjet.
Iz početnih uvjeta imamo
Prvi početni uvjet daje vrijednosti rješenja u prvom vremenskom
nivou 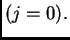 Aproksimacijom derivacije po
Aproksimacijom derivacije po 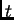 s desna, iz drugog
početnog uvjeta imamo
odakle
Time su, pomoću početnih uvjeta, određene vrijednosti rješenja u
prva dva vremenska nivoa
s desna, iz drugog
početnog uvjeta imamo
odakle
Time su, pomoću početnih uvjeta, određene vrijednosti rješenja u
prva dva vremenska nivoa 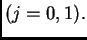 U čvoru
U čvoru 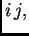 za
za
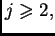 jednadžba je
Nakon množenja s
jednadžba je
Nakon množenja s 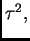 i stavljanja
imamo eksplicitni postupak dan formulom
i stavljanja
imamo eksplicitni postupak dan formulom
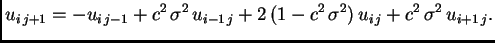 |
(3.35) |
Za
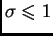 postupak je stabilan.
postupak je stabilan.
2001-10-26
![\begin{displaymath}
% latex2html id marker 41354
\begin{cases}\frac{\textstyle{\...
...al t}} =
\beta{}(x), & \text{za $x \in [0,\ell].$} \end{cases}\end{displaymath}](img3508.png)
![\begin{displaymath}
% latex2html id marker 41354
\begin{cases}\frac{\textstyle{\...
...al t}} =
\beta{}(x), & \text{za $x \in [0,\ell].$} \end{cases}\end{displaymath}](img3508.png)