Exercise 1:

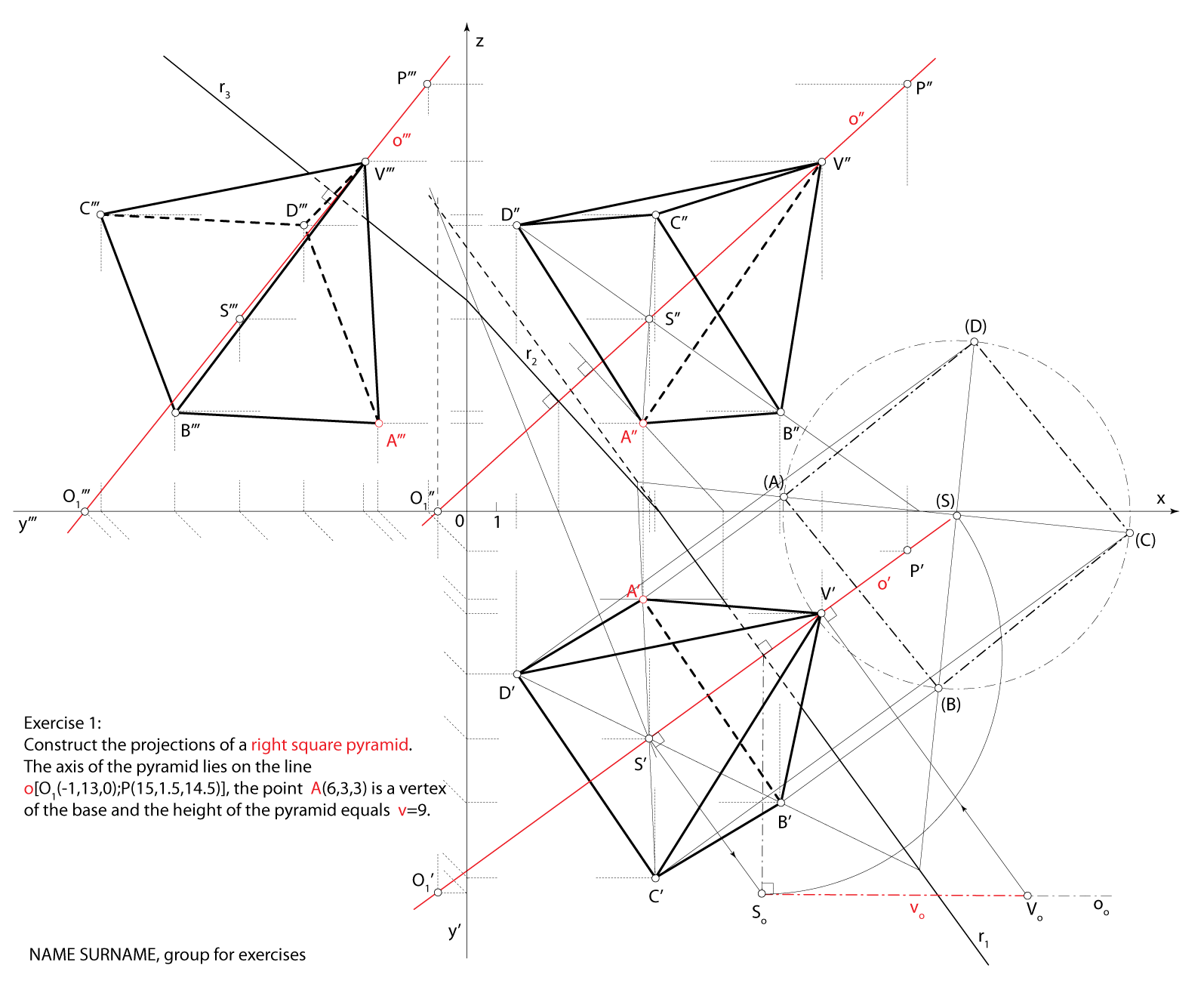
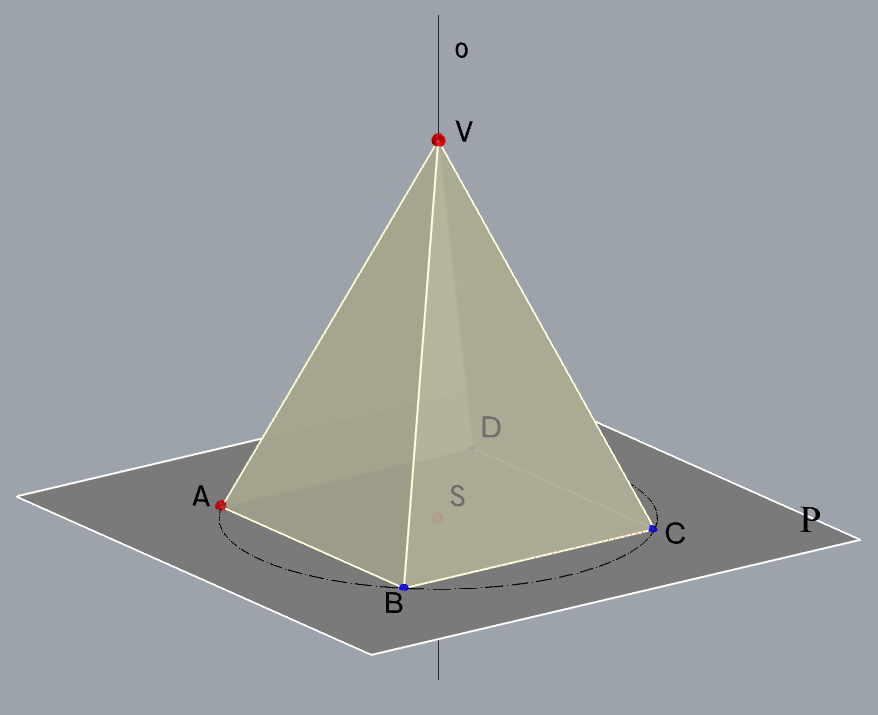
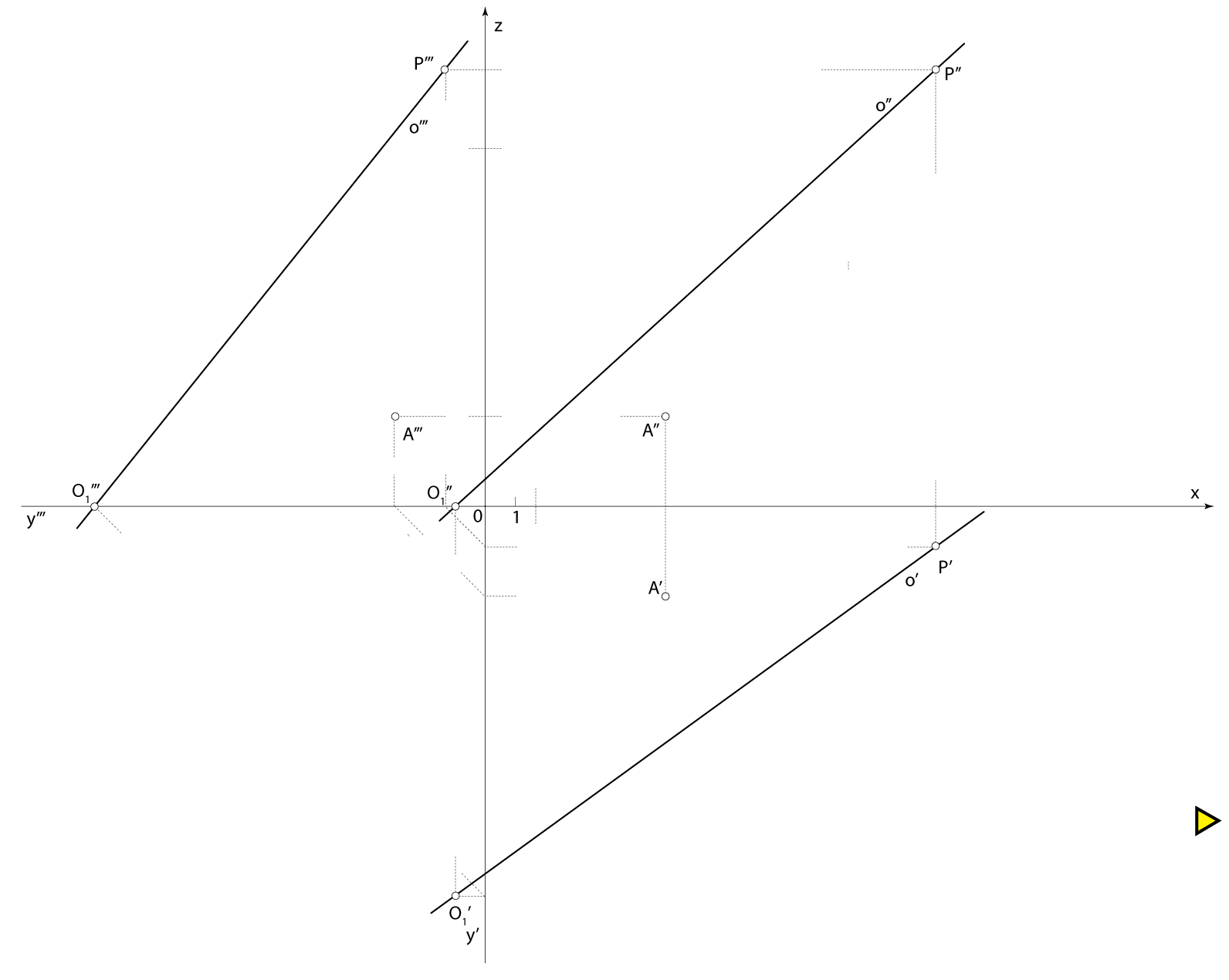
Construct the projections of a right square pyramid. The axis of the pyramid lies on the line \(\small o[O_1(-1,13,0); P(15,1.5,14.5)]\,\,\), the point \(\small A(6,3,3)\) is a vertex of the base and the height of the pyramid equals \(\small v=9\).

Spatial solution

Scheme of spatial solution

  • \(\small\mathrm P\) \(\small -\) plane of the base
    \(\small A\in\,\)\(\small\mathrm P\), \(\small o \perp \) \(\small\mathrm P\)

  • \(\small S-\) center of the base
    \(\small S=o\cap\) \(\small\mathrm P\)

  • \(\small \Box ABCD\subset\,\,\)\(\small\mathrm P\)

  • \(\small V-\) the apex
    \(\small V\in o\), \(\small \,\,d(S,V)=v\)




    • Solution via Monge's method (step by step)


    Final drawing



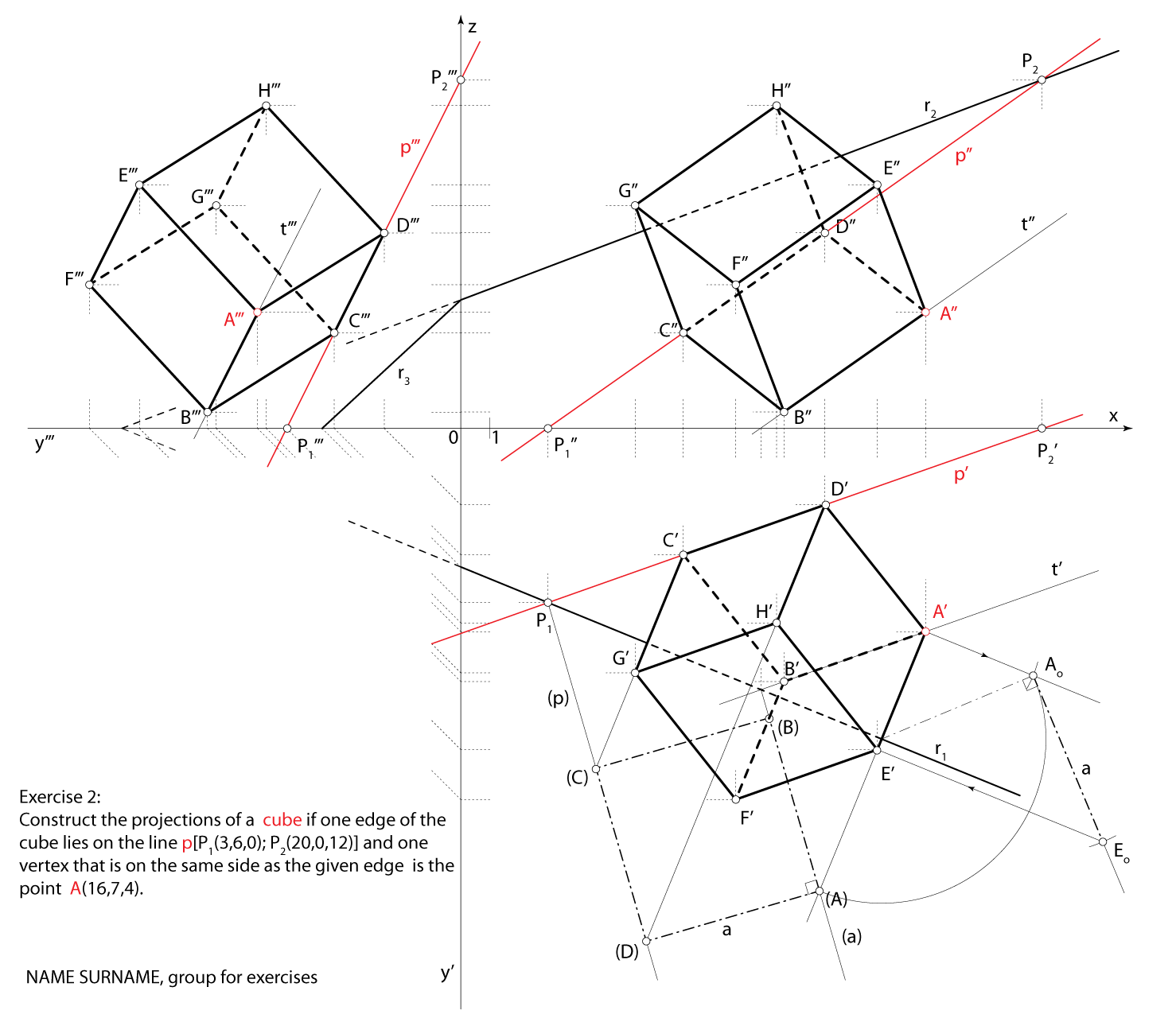
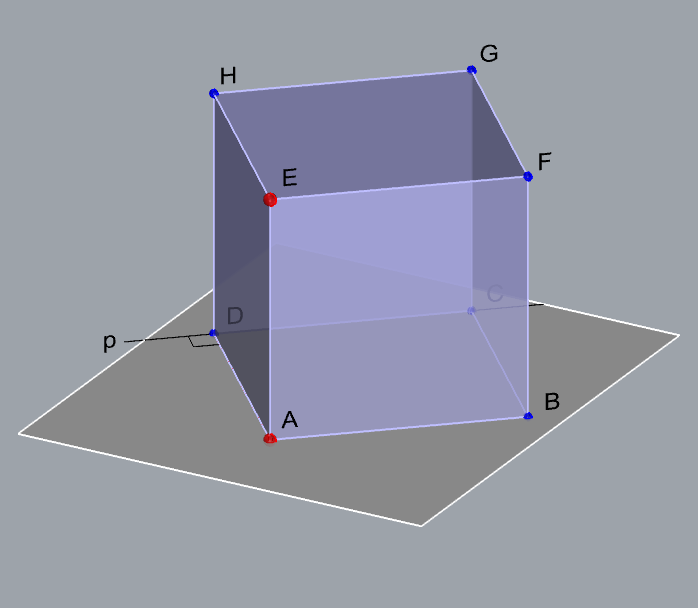
    Exercise 2:

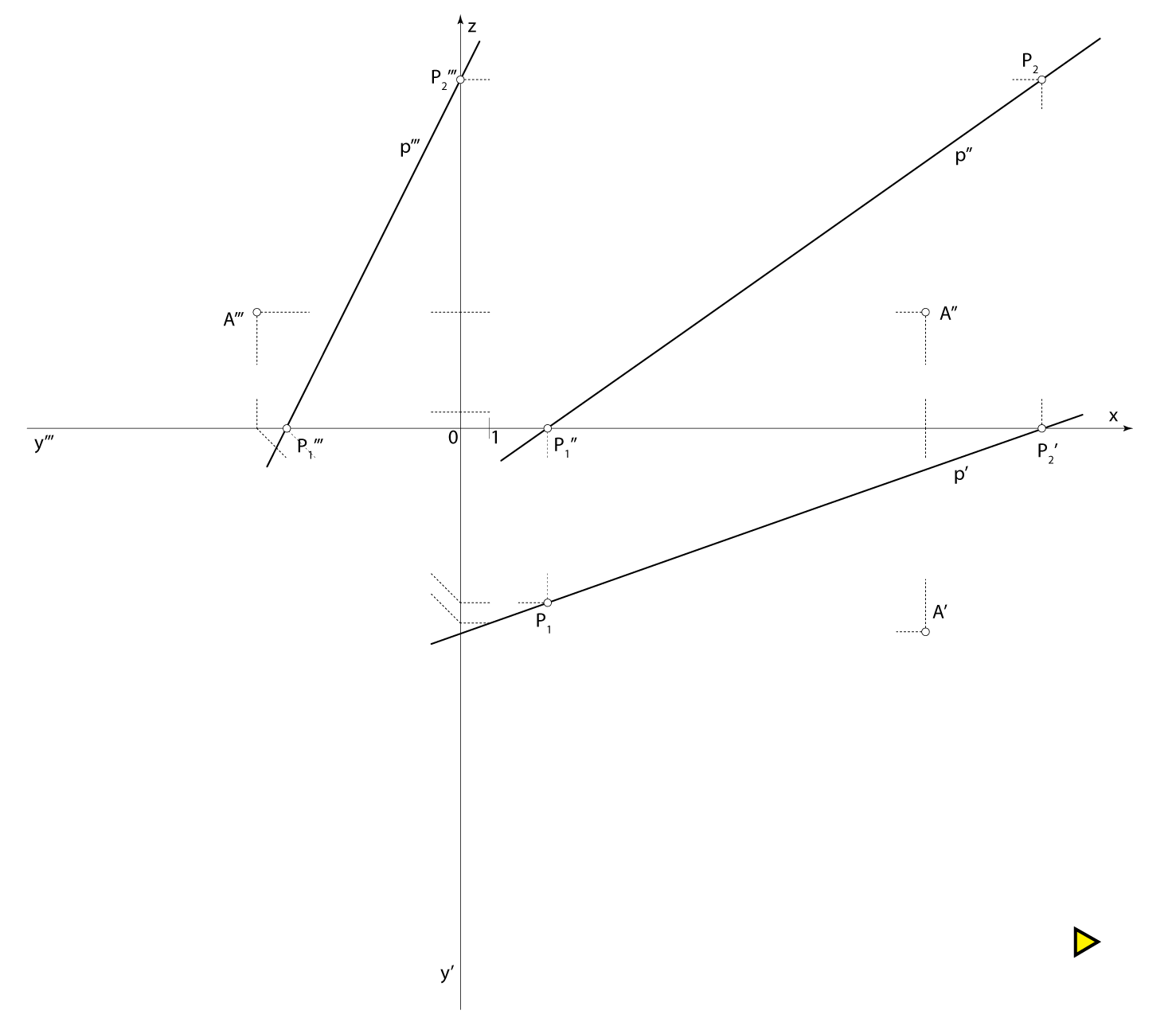
    Construct the projections of a cube if one edge of the cube lies on the line \(\small p[P_1(3,6,0); P_2(20,0,12)]\) and one vertex that is on the same side as the given edge is the point \(\small A(16,7,4)\).

    Spatial solution

    Scheme of spatial solution

  • \(\small\mathrm P\) \(\small -\) plane that contains one side of the cube
    \(\small A\in\) \(\small\mathrm P\), \(\small p \subset \) \(\small\mathrm P\)

  • \(\small \overline{AD}-\) one edge of the cube
    \(\small D\in p\), \(\small \overline{AD}\perp p\)

  • \(\small \Box ABCD\subset\,\,\)\(\small\mathrm P\)

  • \(\small E-\) a vertex of the cube lying in a plane parallel
    to the plane \(\small\mathrm P\)
    \(\small \overline{AE}\perp\,\,\)\(\small\mathrm P\), \(\small \,\,d(A,E)=d(A,D)\)

  • \(\small \Box EFGH\) in a plane parallel to \(\small\mathrm P\)




    • Solution via Monge's method (step by step)


    Final drawing



    Exercise 3:

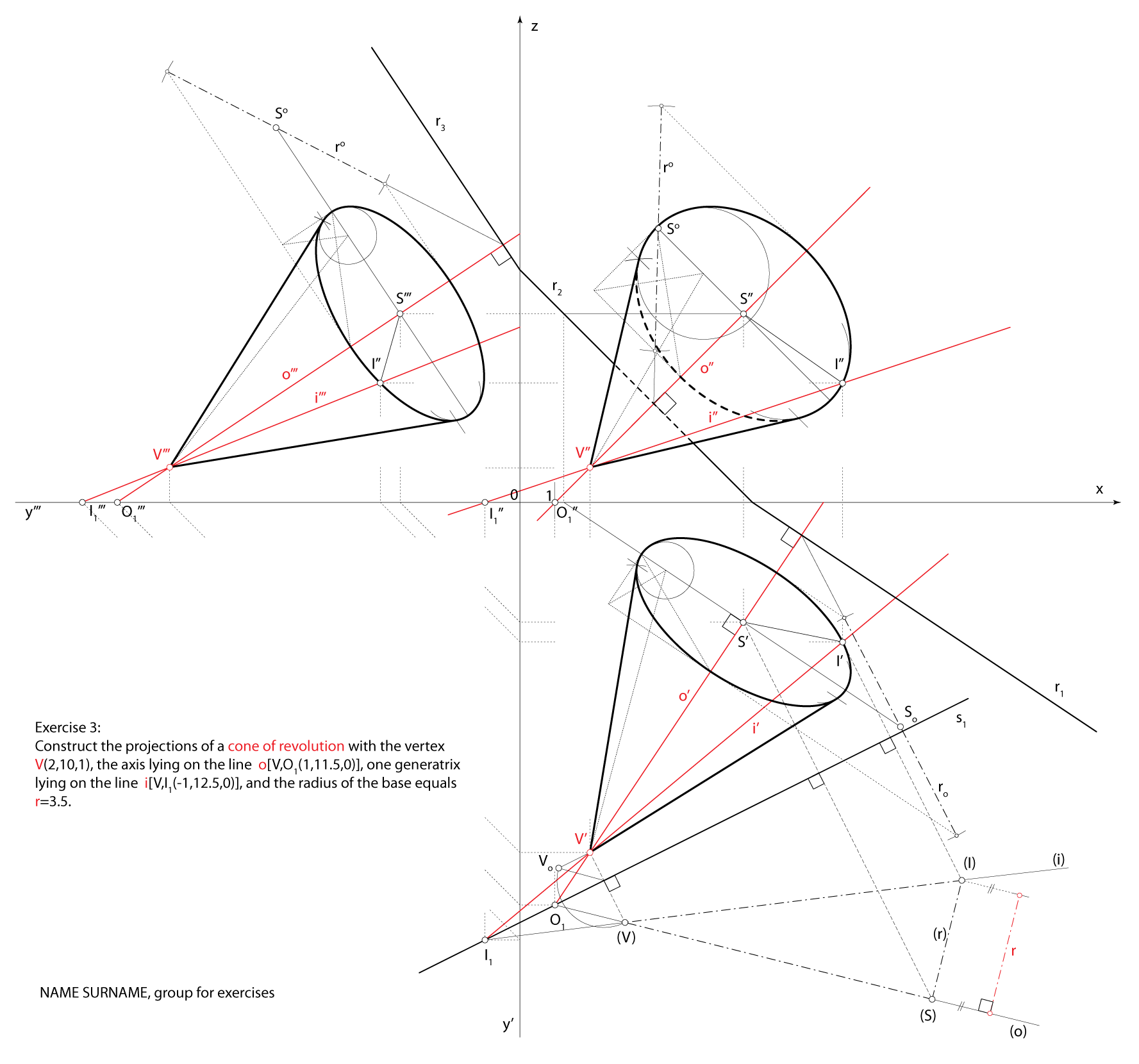
    Construct the projections of a cone of revolution with the vertex \(\small V(2,10,1)\), the axis lying on the line \(\small o [V, O_1(1,11.5,0)]\), one generatrix lying on the line \(\small i [V, I_1(-1,12.5,0)]\) and the radius of the base equal to \(\small r=3.5\).

    Spatial solution

    Scheme of spatial solution

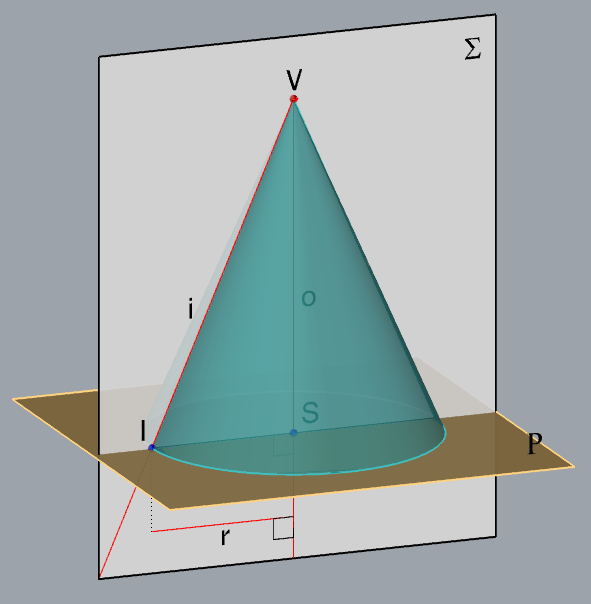
  • \(\small \Sigma\) \(\small -\) axial cross-section plane
    \(\small o\subset \Sigma\), \(\small i\subset \Sigma\)

  • \(\small \triangle ISV \subset \Sigma\)
    \(\small S-\) center of the base
    \(\small I -\) foot of the generatrix \(\small i\)

  • \(\small\mathrm P\) \(\small -\) plane of the base
    \(\small S\in\) \(\small\mathrm P\), \(\small o \perp \) \(\small\mathrm P\)

  • A circle in the plane \(\small\mathrm P\) with center \(\small S\) and
    radius \(\small \overline{SI}\) is the base circle of the given cone.

    • Solution via Monge's method (step by step)


    Final drawing



    Exercise 4:

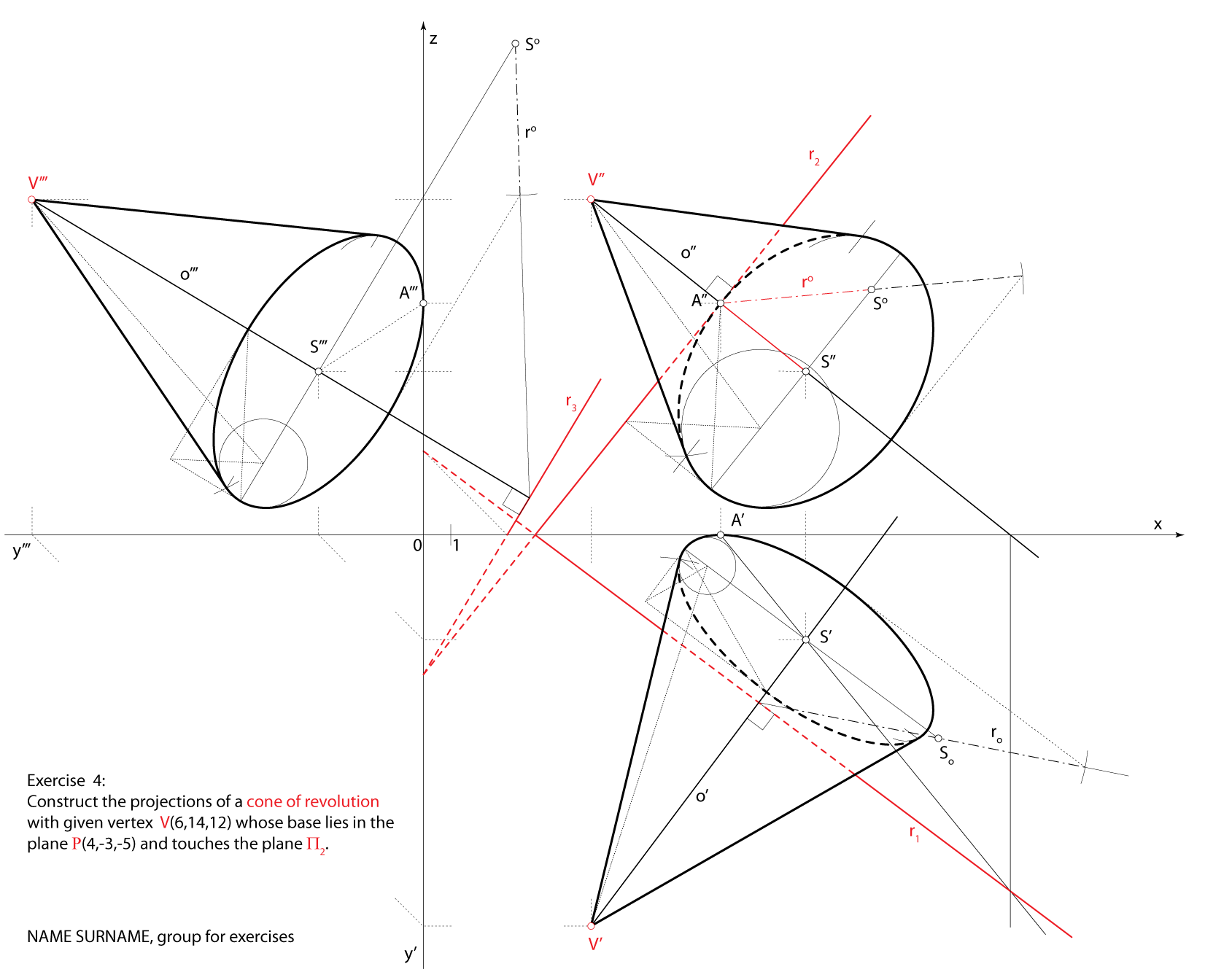
    Construct the projections of a cone of revolution with given vertex \(\small V(6,14,12)\) whose base lies in the plane \(\small\mathrm P\)\(\small (4,-3,-5)\) and touches the plane \(\small \Pi_2\).

    Spatial solution

    Scheme of spatial solution

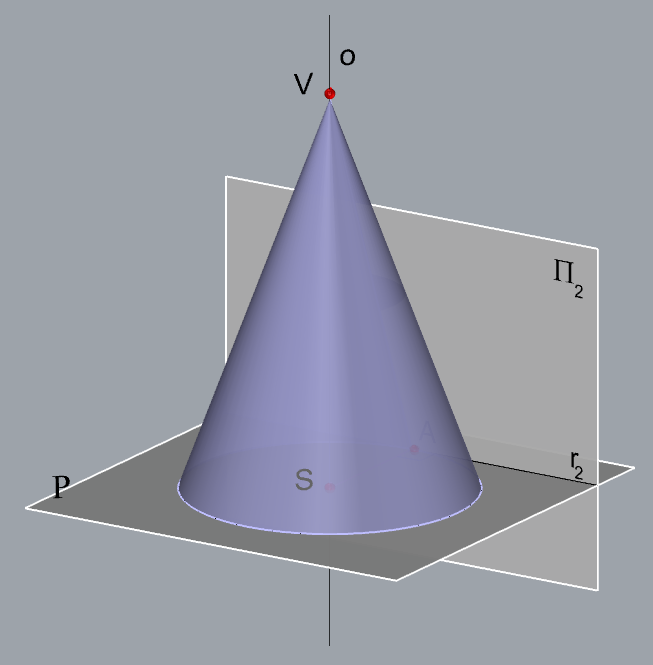
  • \(\small o \,-\) axis of the cone
    \(\small V\in o\), \(\small o \perp\,\) \(\small\mathrm P\)

  • \(\small S \,-\) center of the base
    \(\small S=o\cap\,\)\(\small\mathrm P\)

  • \(\small A \,-\) point on the base circle
    \(\small A\in r_2\), \(\small SA\,\perp\,r_2\)

  • A circle in the plane \(\small\mathrm P\) with center \(\small S\) and radius
    \(\small \overline{SA}\) is the base of the given cone.






    • Solution via Monge's method (step by step)


    Final drawing



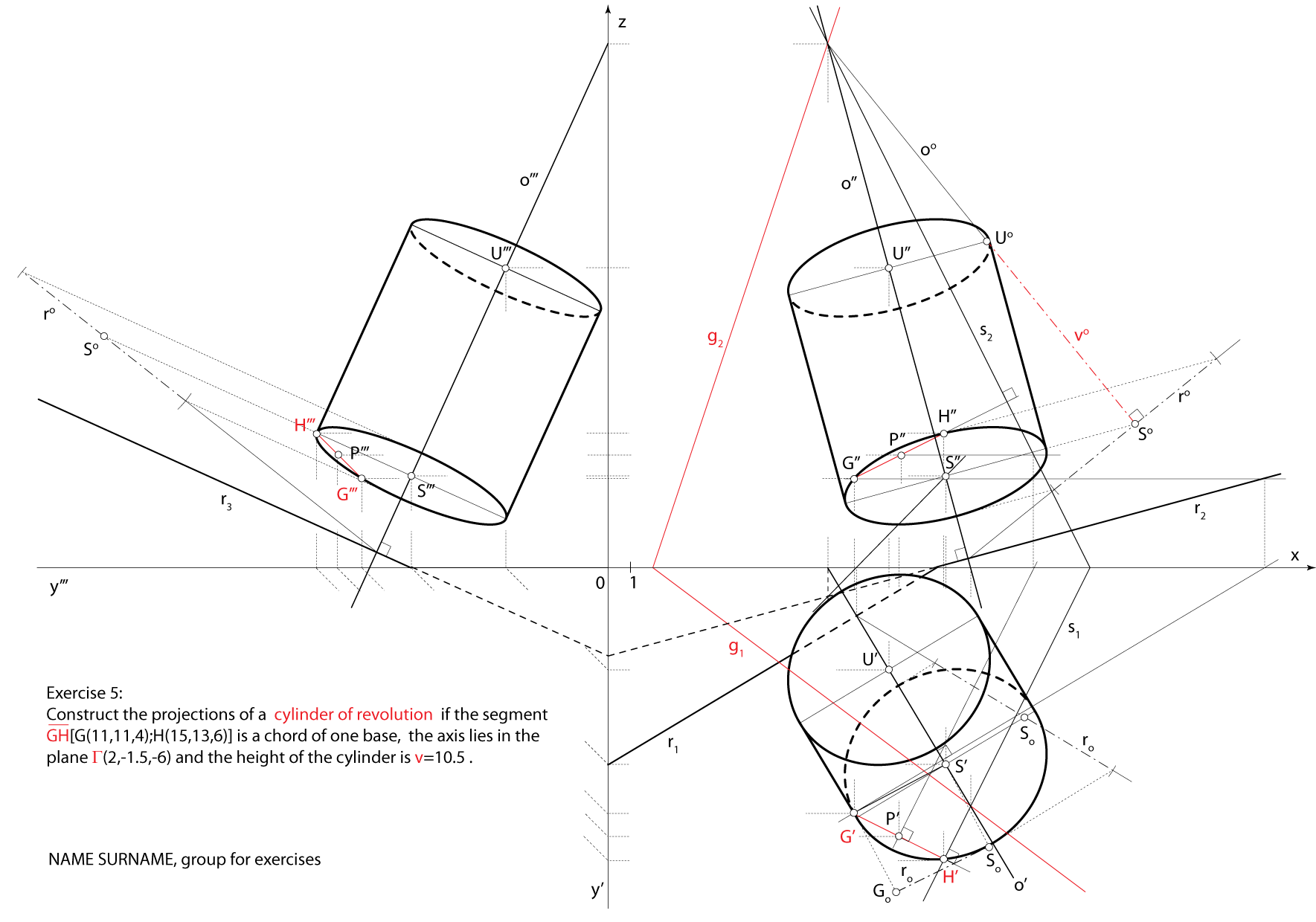
    Exercise 5:

    Construct the projections of a cylinder of revolution if the segment \(\small \overline{GH}[G(11,11,4);H(15,13,6)]\) is a chord of one base, the axis lies in the plane \(\small \Gamma(2,-1.5,-6)\) and the height of the cylinder is \(\small v=10.5\).

    Spatial solution

    Scheme of spatial solution

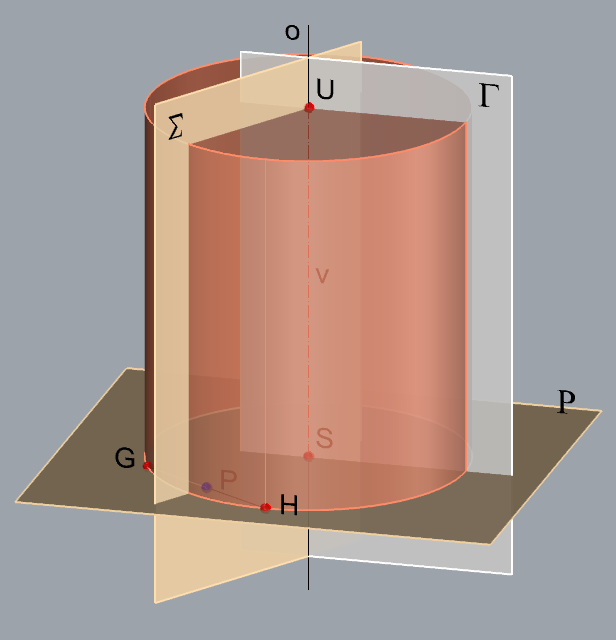
  • \(\small \Sigma -\) bisector plane of the line segment \(\small \overline {GH}\)
    \(\small P -\) midpoint of the line segment \(\small \overline {GH}\),
    \(\small P \in \Sigma\), \(\small \overline {GH} \perp \Sigma\)

  • \(\small o -\) axis of the cylinder, \(\small o = \Sigma \cap \Gamma\)

  • \(\small\mathrm P\)\(\small -\) plane of one base, \(\small G\in \) \(\small\mathrm P\), \(\small o \perp \) \(\small\mathrm P\)

  • \(\small S -\) center of the base, \(\small S = o \cap \) \(\small\mathrm P\)

  • The cirle of the base lies in the plane \(\small\mathrm P\)
    and the radius is \(\small \overline {SG}\).

  • \(\small U -\) center of the other base
    \(\small U \in o \), \(\small d(S,U)=v\).




    • Solution via Monge's method (step by step)


    Final drawing




    Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja