2.1.2. Osnovni stereometrijski odnosi
Međusobni položaj točaka, pravaca i ravnina
Dvije točke mogu se ili podudarati ili biti različite.
Točka i pravac mogu biti u sljedećim položajima:
- \({\small T}\) leži na pravcu \({\small p}\) (\({\small T\in p}\))
- \({\small T}\) ne leži na pravcu \({\small p}\) (\({\small T\notin p}\)).
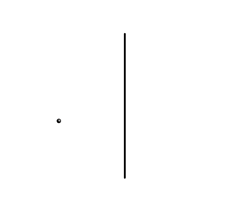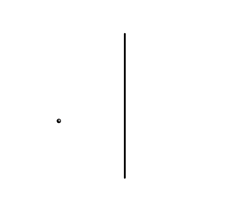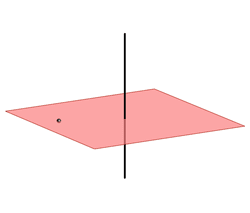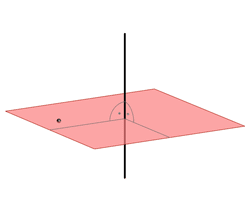
Točka i ravnina mogu biti u sljedećim položajima:
- \({\small T}\) leži u ravnini \({\small\Sigma}\) (\({\small T\in \Sigma}\))
- \({\small T}\) ne leži u ravnini \({\small\Sigma}\) (\({\small T\notin \Sigma}\)).
Dva pravca mogu se ili podudarati ili biti različiti. Ako su različiti, mogu biti u sljedećim položajima:
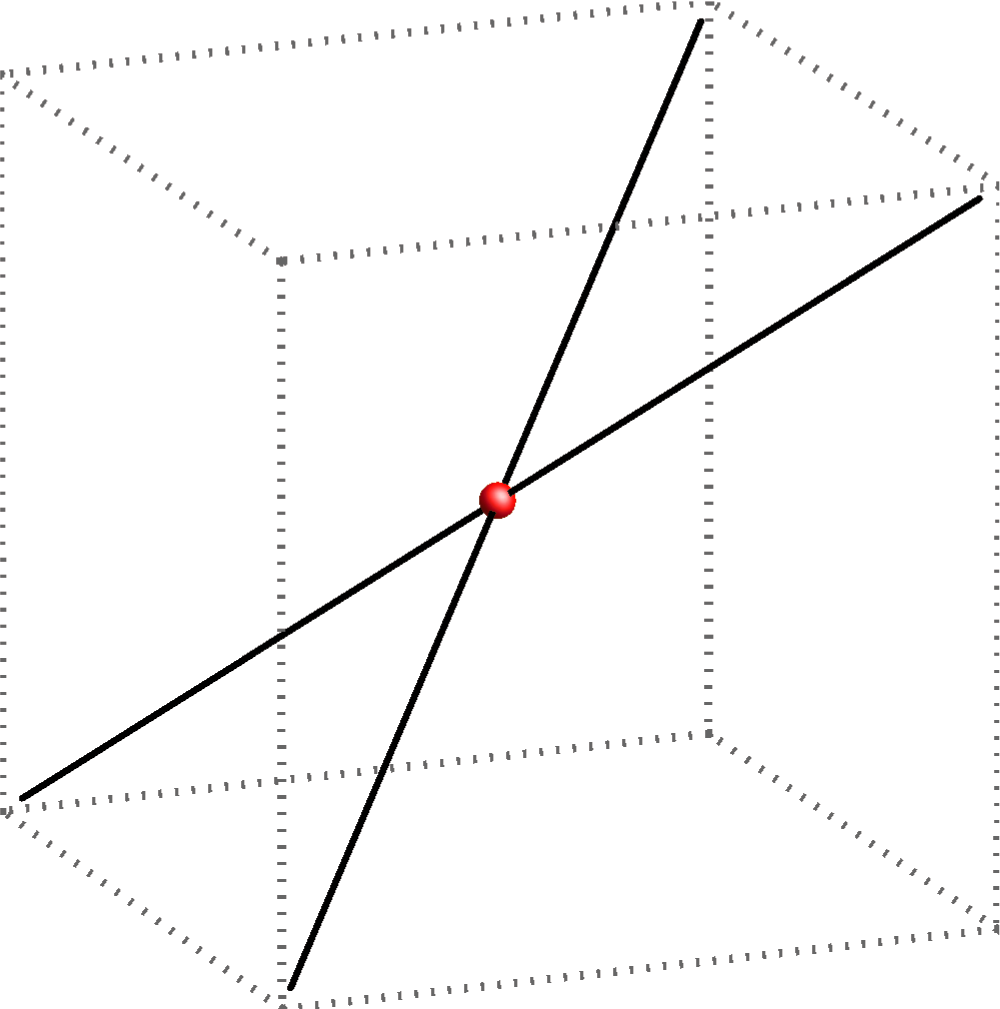
- pravci \({\small p_1}\)i \({\small p_2}\) se sijeku te tada imaju jednu zajedničku točku u konačnosti koju nazivamo njihovim sjecištem,
a za pravce kažemo da su ukršteni ( \({\small p_1\cap p_2 = P}\))
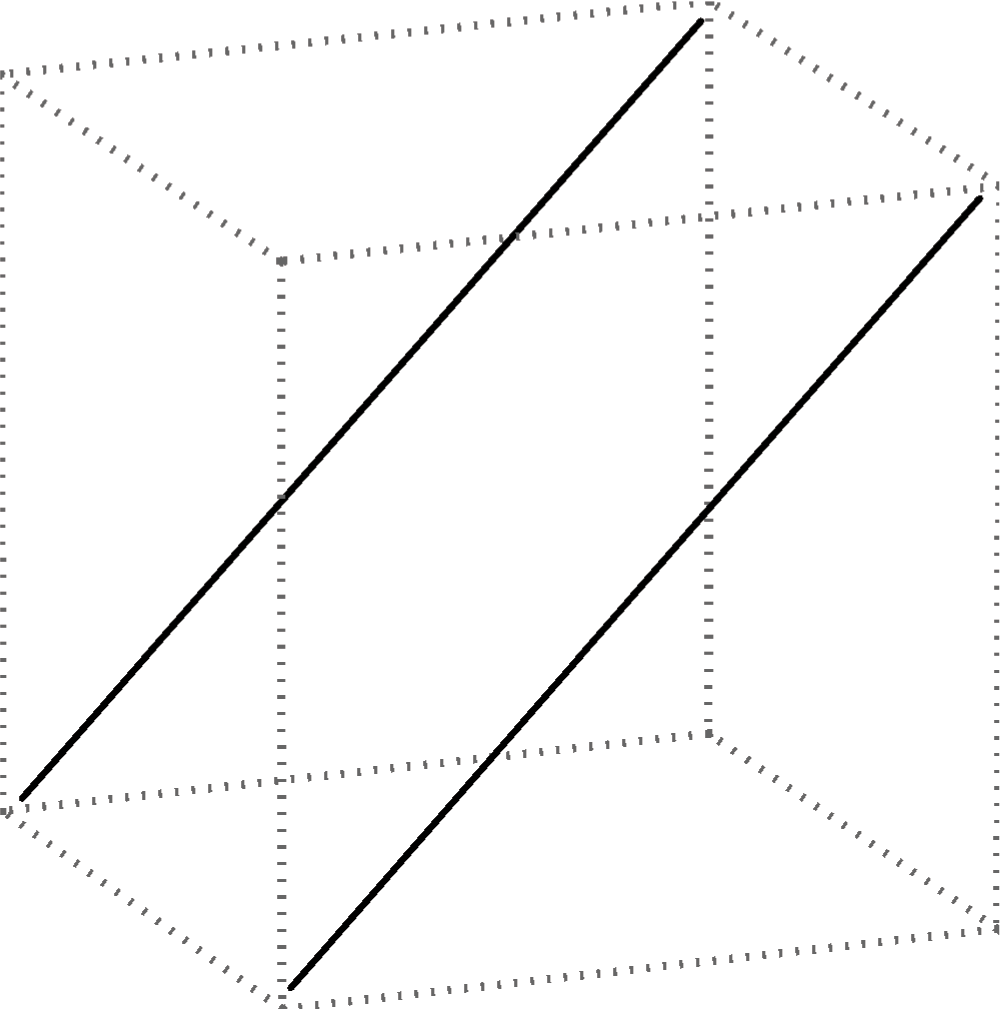
- pravci \({\small p_1}\)i \({\small p_2}\) su paralelni, odnosno njihovo je sjecište neka beskonačno daleka točka (
\({\small p_1 || p_2}\), tj. \({\small p_1\cap p_2 = P^\infty}\)
)
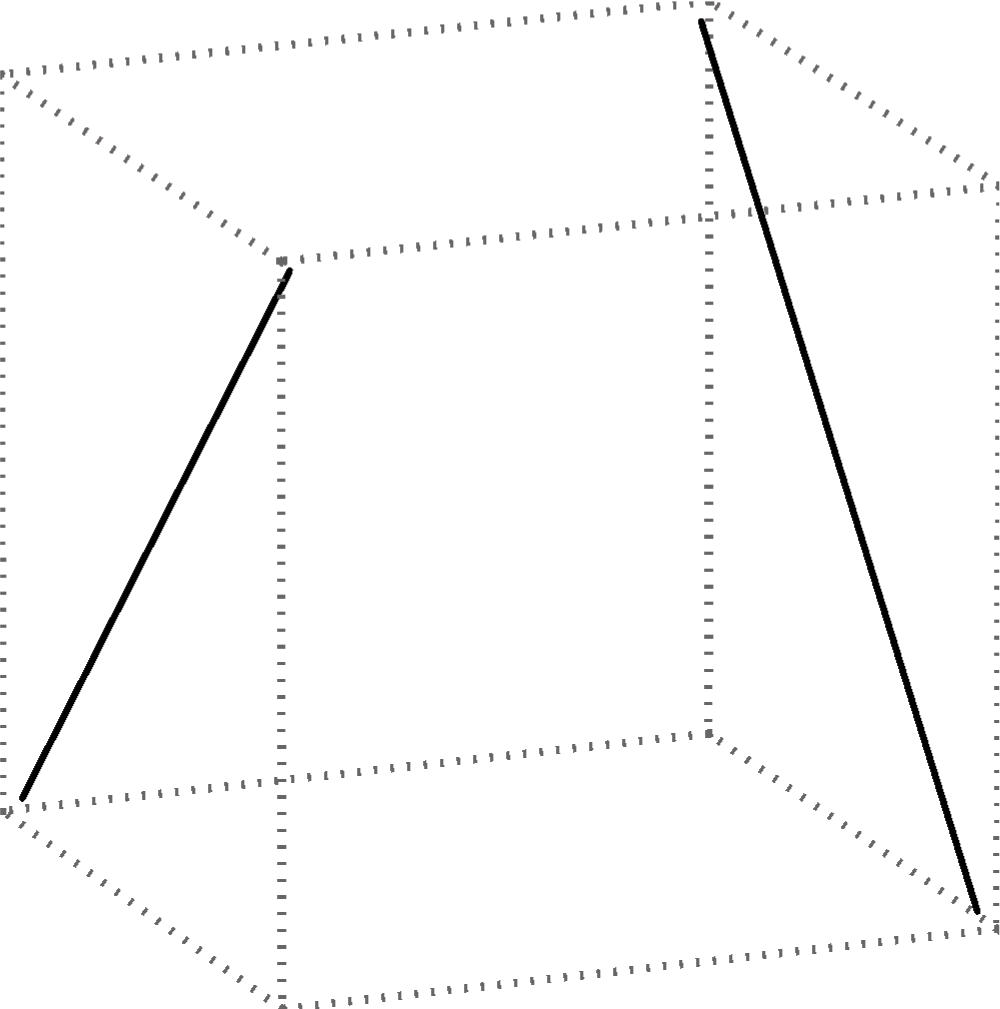
- pravci \({\small p_1}\)i \({\small p_2}\) su mimosmjerni ili mimoilazni te tada nemaju ni jednu zajedničku točku (\({\small p_1\cap p_2 = \phi}\)).
|
|
|
|
|
Slika 18: Pravci se sijeku (ukršteni)
|
Slika 19: Paralelni pravci
|
Slika 20: Mimosmjerni pravci
|
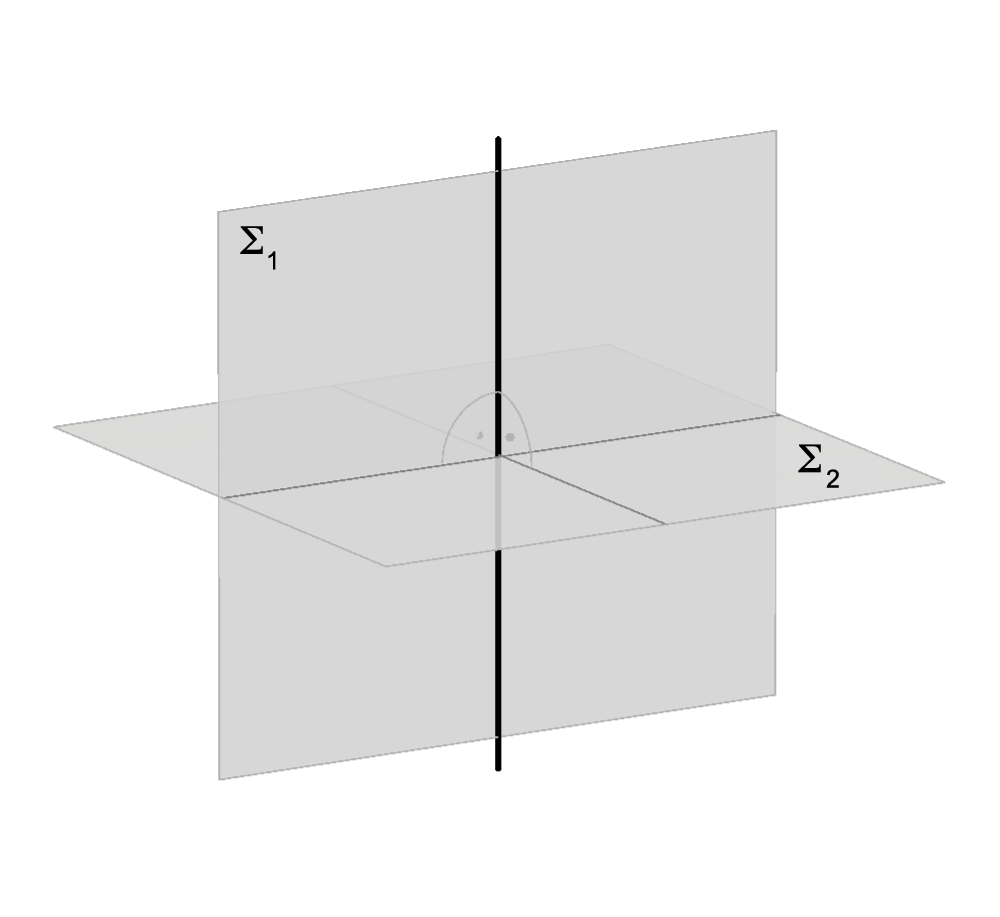
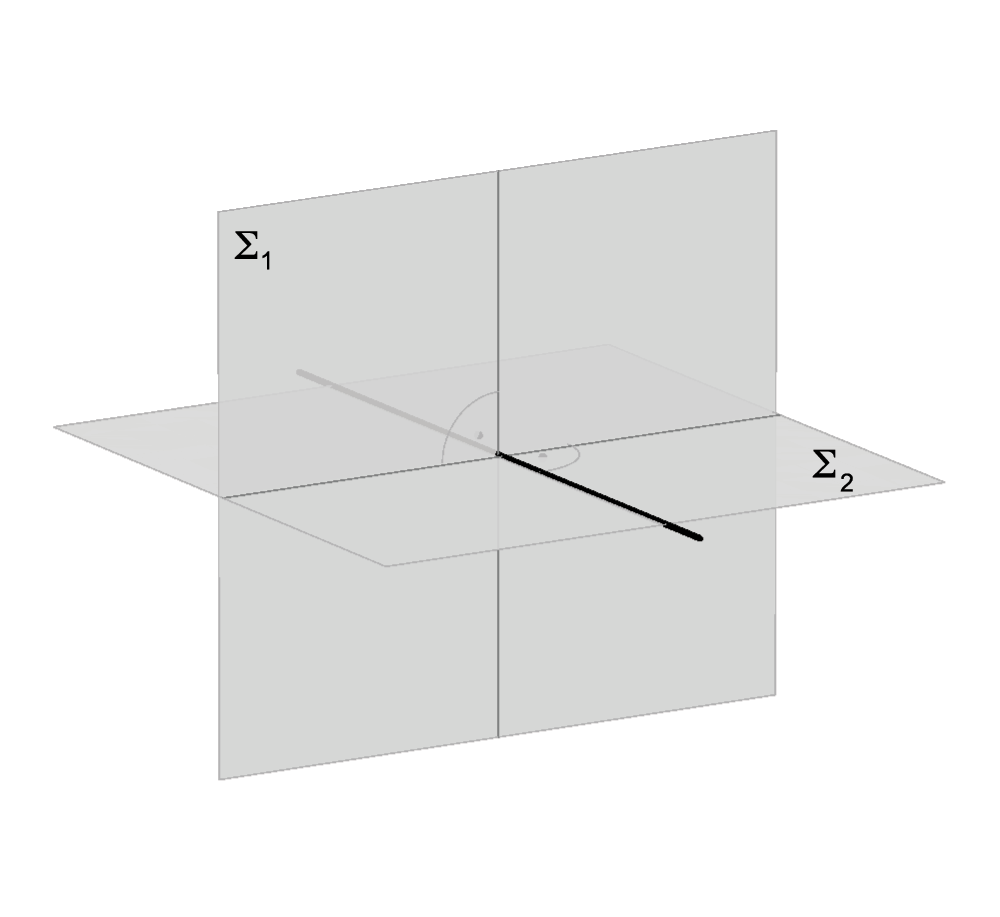
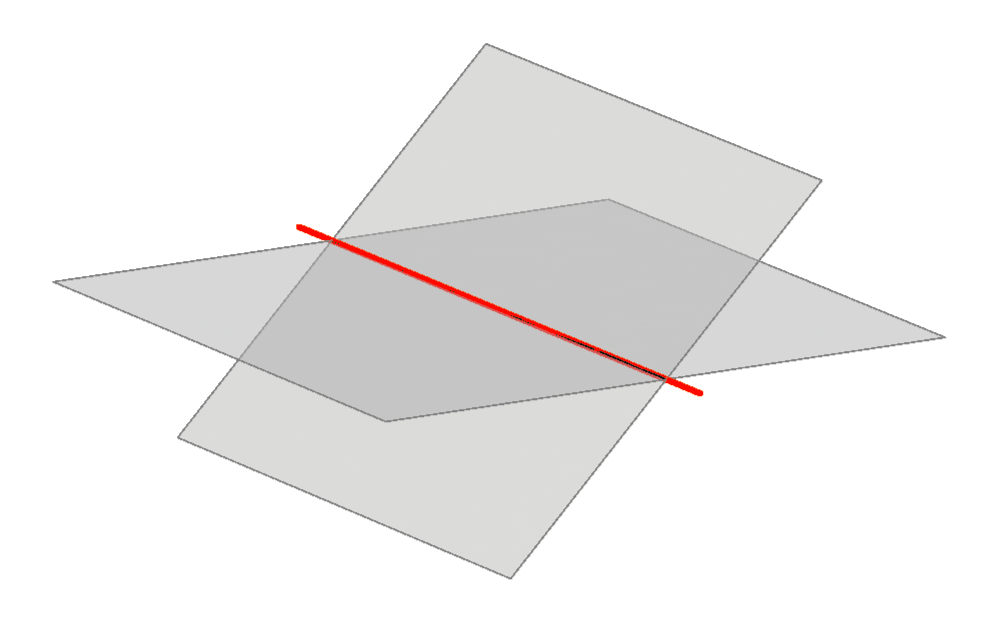
Dvije ravnine mogu se ili podudarati ili biti različite. Ako su različite, mogu biti u sljedećim položajima:
- ravnine \({\small \Sigma_1}\) i \({\small \Sigma_2}\) se sijeku te tada imaju jedan zajednički pravac kojeg nazivamo njihovom presječnicom (\({\small \Sigma_1\cap \Sigma_2 =p}\))
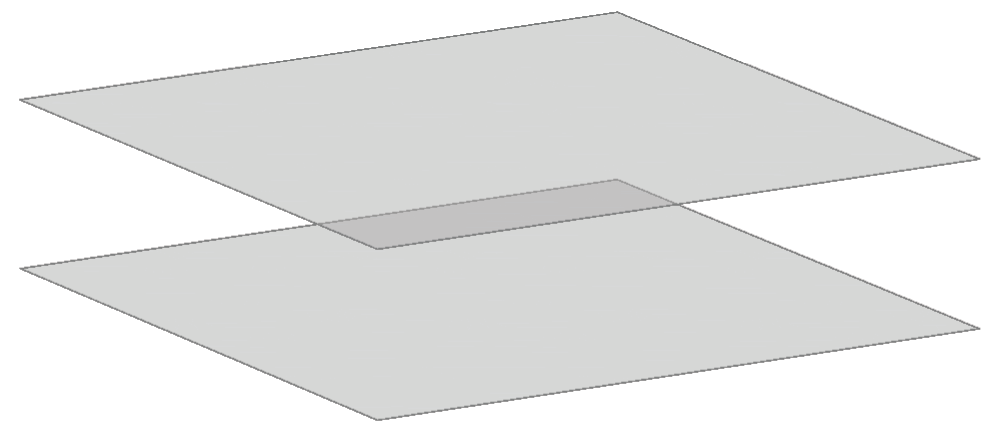
- ravnine \({\small \Sigma_1}\) i \({\small \Sigma_2}\) su paralelne, odnosno njihova je presječnica neki beskonačno daleki pravac prostora (\({\small \Sigma_1\parallel \Sigma_2}\), tj. \({\small \Sigma_1\cap \Sigma_2 = p^\infty}\)).
|
|
|
|
Slika 21: Ravnine se sijeku duž presječnice
|
Slika 22: Paralelne ravnine
|
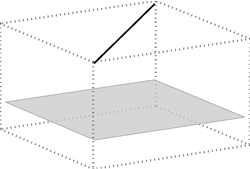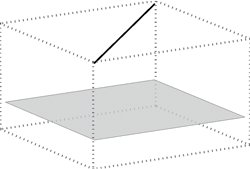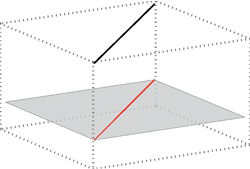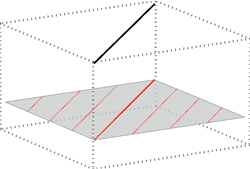
Pravac i ravnina u prostoru mogu biti u sljedećim položajima:
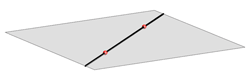
- pravac \({\small p}\) leži u ravnini \({\small \Sigma}\), odnosno ako dvije različite točke pravca \({\small p}\) leže u ravnini \({\small \Sigma}\), onda i pravac \({\small p}\) leži u ravnini \({\small \Sigma}\),
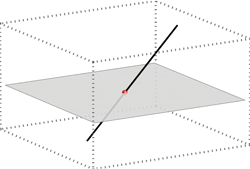
(\({\small p\subset\Sigma}\)) - pravac \({\small p}\) i ravnina \({\small \Sigma}\) se sijeku - tada pravac i ravnina imaju jednu zajedničku točku u konačnosti koju nazivamo njihovim probodištem (\({\small p\cap\Sigma =P}\))
- pravac \({\small p}\) i ravnina \({\small \Sigma}\) su paralelni, odnosno njihovo je probodište beskonačno daleka točka ( \({\small p\parallel\Sigma}\), tj. \({\small p\cap\Sigma =P^\infty}\)).
Pravac \({\small p}\) paralelan je s ravninom \({\small \Sigma}\) ako u \({\small \Sigma}\) postoji barem jedan pravac koji je paralelan s pravcem \({\small p}\). Tada vrijedi da u ravnini \({\small \Sigma}\) postoji beskonačno mnogo pravaca koji su paralelni s pravcem \({\small p}\). Oni čine pramen paralelnih pravaca u toj ravnini.
|
|
Slika 23: Pravac leži u ravnini
|
Slika 24: Pravac probada ravninu u probodištu
|
Animacija 2: Pravac je paralelan s ravninom
|
Određenost ravnine
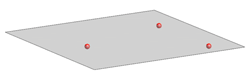
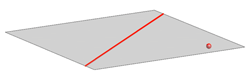
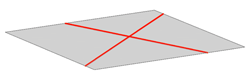
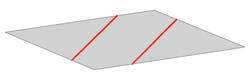
Ravnina je jednoznačno određena s:
- tri nekolinearne točke
- jednim pravcem i jednom točkom koja ne leži na tom pravcu
- dva pravca koji se sijeku
- dva paralelna pravca.
|
|
|
|
|
|
Slika 25
|
Slika 26 |
Slika 27 |
Slika 28 |
Za točke i pravce koji leže u istoj ravnini kažemo da su komplanarni.
Dva mimosmjerna pravca ne mogu ležati u istoj ravnini pa stoga mimosmjerni pravci nikada nisu komplanarni.
Mjerenje kuta i okomitost
Kut između pravaca i okomiti (ortogonalni) pravci
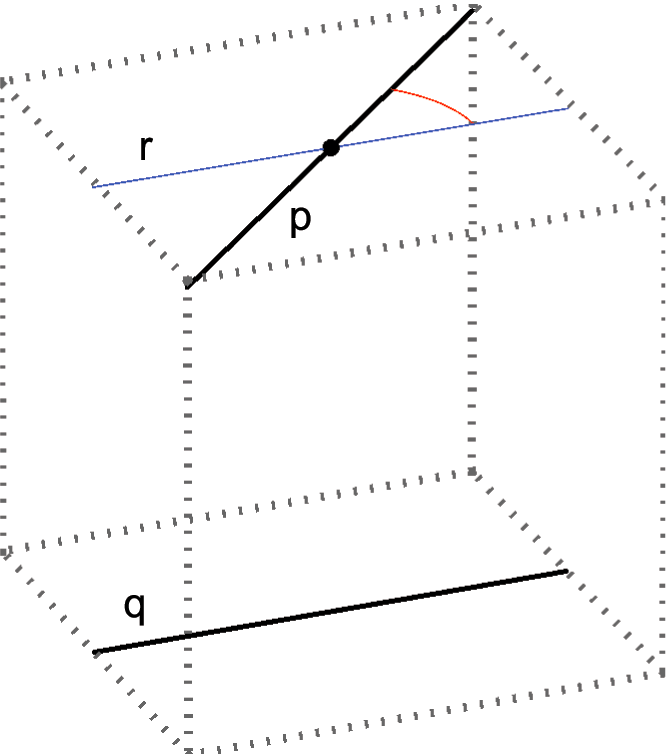
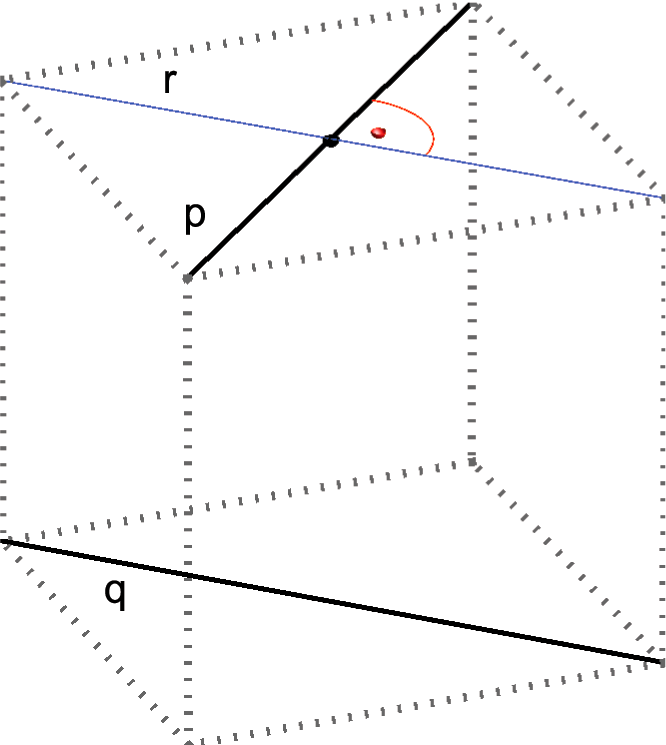
Kut između dva pravca koji leže u istoj ravnini učili ste mjeriti još u osnovnoj školi. Znate da je kut između dva okomita pravca mjere \({\small 90^\circ}\) (pravi), a onaj između paralelnih pravaca mjere \({\small 0^\circ}\). U svim ostalim slučajevima mjera kuta je između te dvije vrijednosti. Ovdje ćemo mjerenje kuta proširiti i na pravce koji ne leže u istoj ravnini, dakle na mimosmjerne pravce. To činimo na sljedeći način:
- Neka su \({\small p}\) i \({\small q}\) dva mimosmjerna pravca. Na bilo kojem od tih pravaca odaberemo jednu točku i kroz nju položimo pravac
\({\small r}\) koji je paralelan s drugim. Kut između tako dobivenih ukrštenih pravaca jednak je kutu između mimosmjernih pravaca \({\small p}\) i \({\small q}\).
- Mimosmjerni pravci su okomiti (ortogonalni) ako je kut između njih (prema navedenoj definiciji) pravi.
|
|
|
|
Slika 29: \({\small q\parallel r,\,\,\angle (p,q)=\angle (p,r)}\)
|
Slika 30: \({\small q\parallel r,\,\,p\perp r \Rightarrow p\perp q}\)
|
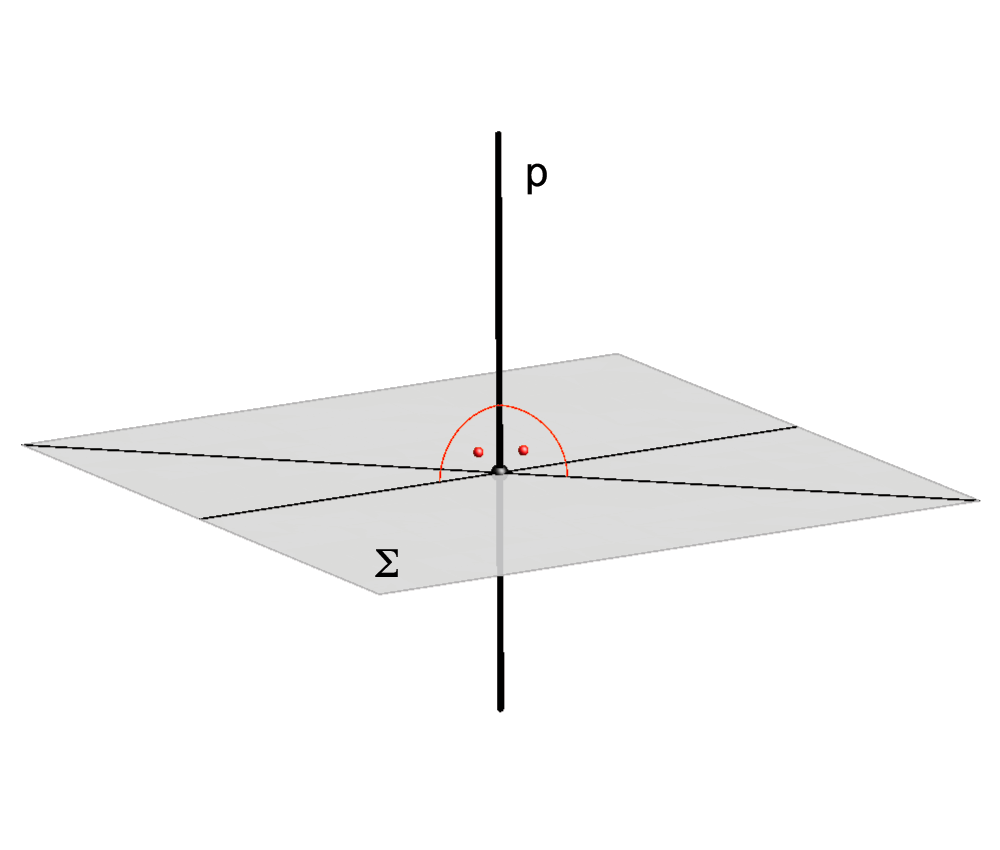
Okomitost pravca i ravnine
- Pravac \({\small p}\) je okomit (ortogonalan) na ravninu \({\small\Sigma}\) ako je okomit na svaki pravac u toj ravnini.
Pravac \({\small p}\) nazivamo okomicom ili normalom ravnine \({\small\Sigma}\), a probodište pravca \({\small p}\) i ravnine \({\small\Sigma}\) nožištem pravca \({\small p}\). Međutim, jasno je da nije potrebno (a ni moguće) provjeravati okomitost za sve pravce ravnine, pa se postavlja pitanje koji su dovoljni uvjeti da pravac i ravnina budu okomiti. Odgovor je dan u sljedećem teoremu kojeg ovdje nećemo dokazivati:
- Pravac \({\small p}\) okomit je na ravninu \({\small\Sigma}\) ako je okomit na bilo koja dva ukrštena pravca te ravnine. Vidi sliku
31.
Usto ističemo još dva važna teorema (intuitivno vrlo jasna), koji su vezani za okomitost pravca i ravnine:
- Svakom točkom prostora prolazi jedinstvena ravnina koja je okomita na dani pravac. Vidi animaciju
3.
- Svakom točkom prostora prolazi jedinstvena okomica dane ravnine. Vidi animaciju
4.
|
|
Slika 31
|
Animacija 3
|
Animacija 4
|
Okomitost dviju ravnina
- Dvije su ravnine okomite ako jedna od tih ravnina sadrži barem jedan pravac koji je okomit na drugu ravninu.
Tu činjenicu možemo i ovako zapisati: \({\small \Sigma_1\perp\Sigma_2\Longleftrightarrow \exists p\subset \Sigma_1,\,\, p\perp\Sigma_2}\)
Relacija okomitosti je simetrična, odnosno ako je \({\small \Sigma_1\perp\Sigma_2}\), onda je i \({\small \Sigma_2\perp\Sigma_1}\). Stoga i u ravnini \({\small \Sigma_2}\) postoji pravac koji je okomit na ravninu \({\small \Sigma_1}\). Štoviše, ako su dvije ravnine okomite, tada svaka od njih sadrži beskonačno mnogo pravaca (pramen paralelnih pravaca) koji su okomiti na drugu ravninu.
|
|
Slika 32: \({\small \Sigma_1\perp\Sigma_2}\)
|
Slika 33: \({\small \Sigma_2\perp\Sigma_1}\)
|
Ortogonalna projekcija
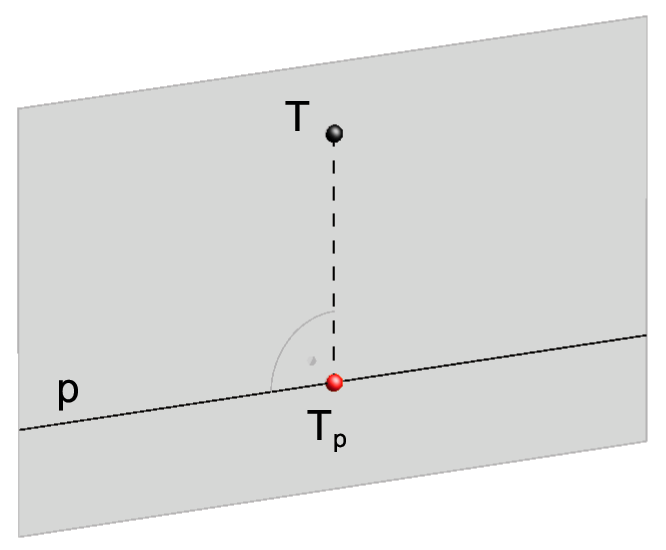
- Ortogonalna projekcija \({\small T_p}\), točke \({\small T}\) na pravac \({\small p}\), sjecište je pravca \({\small p}\) i okomice iz \({\small T}\) na \({\small p}\) koja leži u ravnini određenoj s \({\small T}\) i \({\small p}\). Ako \({\small T}\) leži na pravcu \({\small p}\), onda je \({\small T_p=T}\).
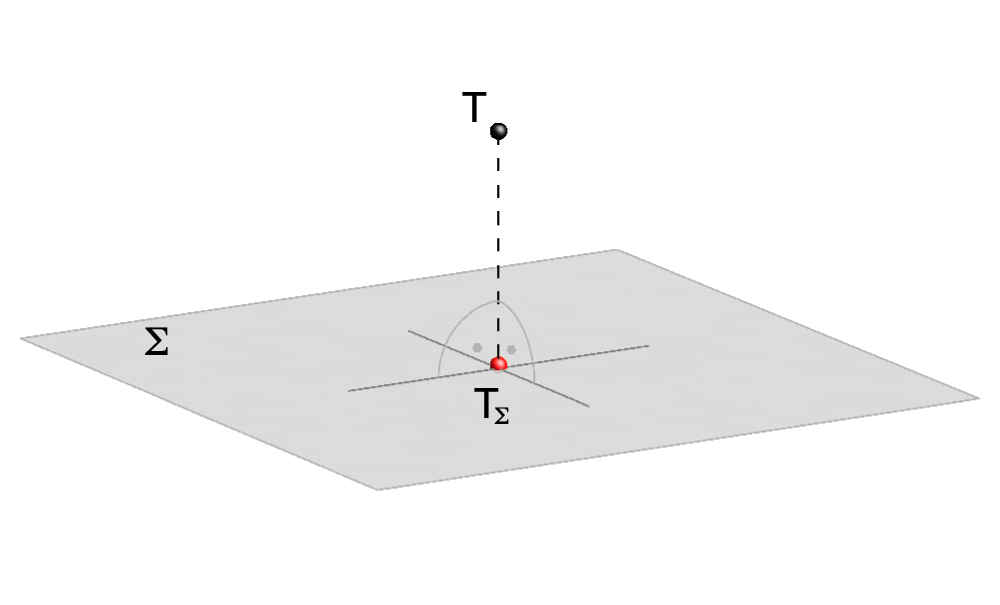
- Ortogonalna projekcija \({\small T_\Sigma}\), točke \({\small T}\) na ravninu \({\small \Sigma}\), probodište je ravnine \({\small \Sigma}\) i pravca koji prolazi točkom \({\small T}\), a okomit je na \({\small \Sigma}\). Ako \({\small T}\) leži u ravnini \({\small \Sigma}\), onda je \({\small T_\Sigma=T}\).
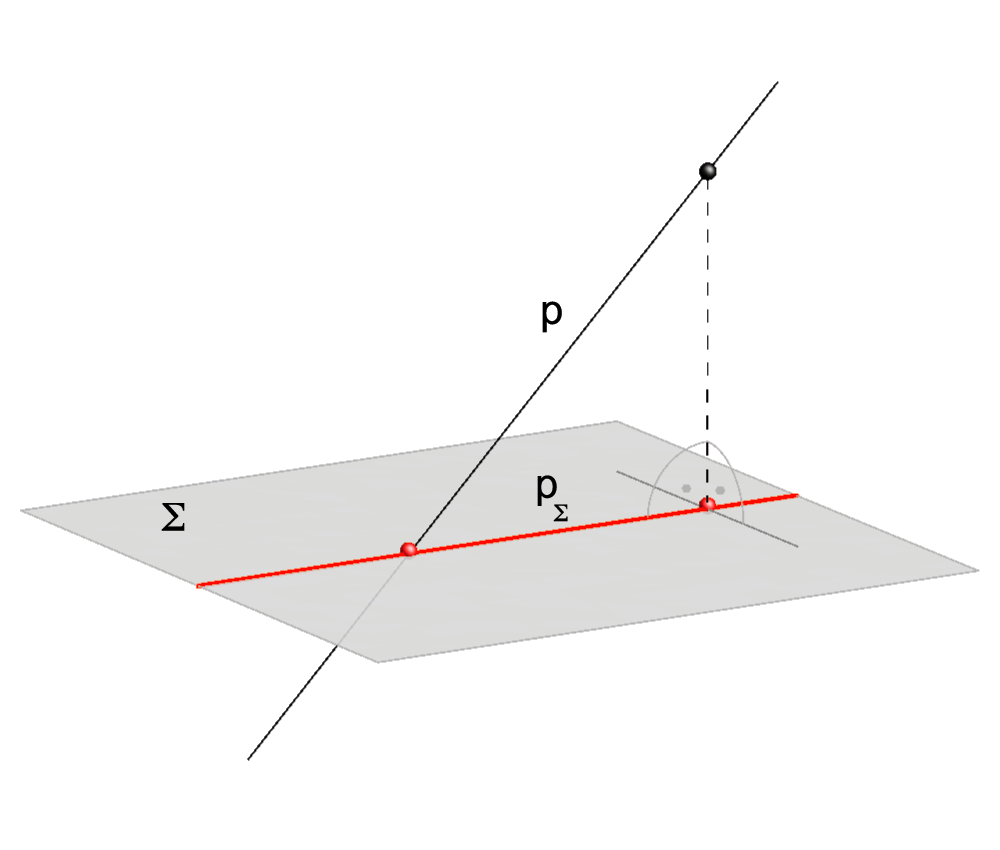
- Ortogonalna projekcija \({\small p_\Sigma}\), pravca \({\small p}\) na ravninu \({\small \Sigma}\), skup je ortogonalnih projekcija svih točaka pravca \({\small p}\) na ravninu \({\small \Sigma}\). Ako je pravac \({\small p}\) okomit na ravninu \({\small \Sigma}\), onda je njegova ortogonalna projekcija točka (\({\small T_\Sigma = p\cap \Sigma}\)). U svim ostalim slučajevima \({\small p_\Sigma}\) je pravac. Ako pravac \({\small p}\) leži u ravnini \({\small \Sigma}\), onda je \({\small p_\Sigma=p}\).
|
|
|
|
|
Slika 34: Ortogonalna projekcija točke
na pravac
|
Slika 35: Ortogonalna projekcija točke
na ravninu
|
Slika 36: Ortogonalna projekcija pravca
na ravninu
|
Kut između pravca i ravnine
Za pravac koji nije okomit na ravninu vrijedi:
- Kut između pravca i ravnine jednak je kutu između pravca i njegove ortogonalne projekcije na tu ravninu - \({\small \angle (p,\Sigma)=\angle (p,p_\Sigma)}\).
Sasvim je razumljivo da ako pravac leži u ravnini ili je s njom paralelan, kut između pravca i ravnine je \({\small 0^\circ}\). Ako je pravac okomit na ravninu, kut između njih je \({\small 90^\circ}\).
|
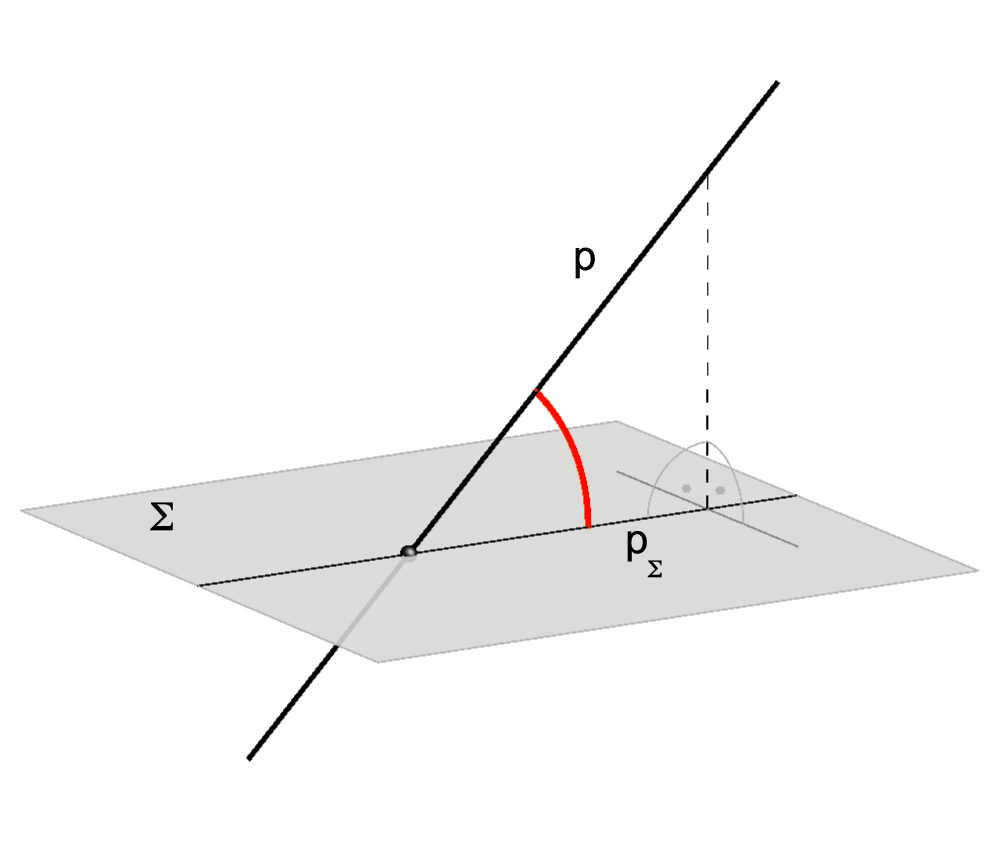
Slika 37: Kut između pravca i ravnine
|
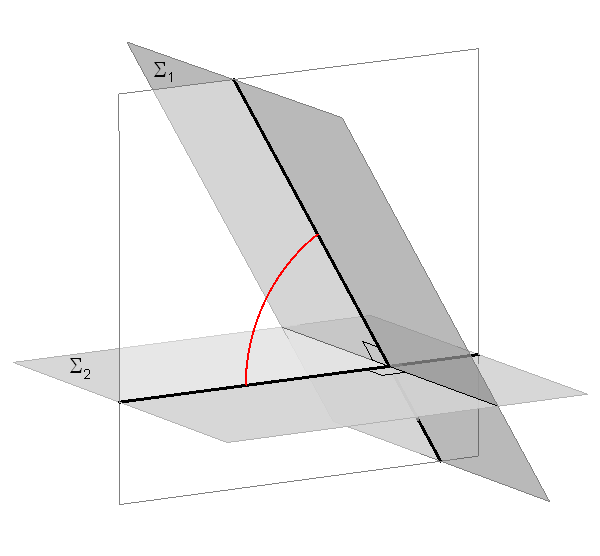
Kut između dvije ravnine
- Kut između paralelnih ravnina je \({\small 0^\circ}\).
Kao definiciju kuta između dvije ravnine koje se sijeku možemo odabrati jednu od sljedeće dvije izjave:
- Kut između dviju ravnina koje se sijeku jednak je kutu između bilo koja dva pravca koji leže u tim ravninama (po jedan u svakoj od njih), a okomiti su na njihovu presječnicu.
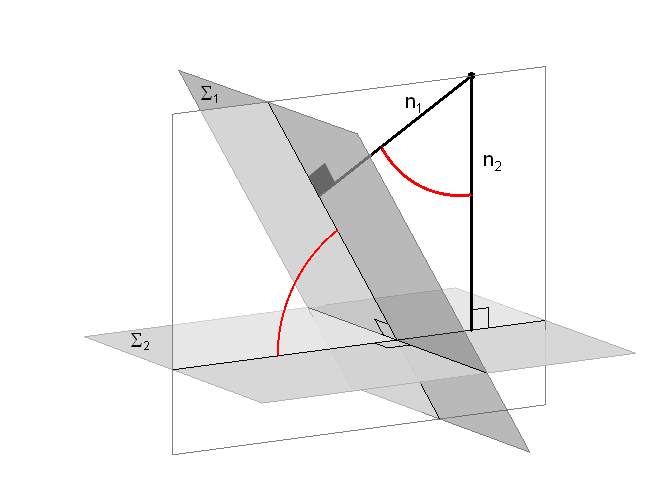
- Kut između dviju ravnina koje se sijeku, jednak je kutu između njihovih normala.
|
|
|
|
Slika 38: Ukršteni pravci pomoću kojih mjerimo kut leže u bilo kojoj ravnini okomitoj na presječnicu danih ravnina
|
Slika 39: Kut između dviju ravnina jednak je kutu između njihovih normala
|
Udaljenost
Udaljenost između dviju točaka
Mjerenje udaljenosti između dviju točaka \({\small T_1}\) i \({\small T_2}\) vjerojatno je prvo mjerenje s kojim ste se u životu susreli.
Ta je udaljenost jednaka duljini dužine kojoj su krajevi točke \({\small T_1}\) i \({\small T_2}\).
Broj koji izražava tu udaljenost označavamo \({\small d(T_1,T_2)}\).
Ako je \({\small T_1=T_2}\), onda je \({\small d(T_1,T_2)=0}\).
Udaljenost između dva skupa točaka
Udaljenost dva skupa točaka \(\mathrm A\) i \(\mathrm B\) je najkraća udaljenost među točkama tih skupova.
\({\small d(}\)\(\mathrm{A, B}\)\({\small) = \mathrm{min} \{d(A,B) | A\in}\)\( \mathrm A\), \({\small B\in}\)\(\mathrm B\)\({\small \}}\).
Udaljenost između točke i pravca
Udaljenost između točke \({\small T}\) i pravca \({\small p}\) je udaljenost točke \({\small T}\) od njezine ortogonalne projekcije na taj pravac, dakle \({\small d(T,p) = d(T,T_p)}\).
Udaljenost između točke i ravnine
Udaljenost između točke \({\small T}\) i ravnine \({\small \Sigma}\) je udaljenost točke \({\small T}\) od njezine ortogonalne projekcije na tu ravninu, odnosno \({\small d(T,\Sigma) = d(T,T_\Sigma)}\).
Udaljenost između dva pravca
- Ako se pravci sijeku, njihova je udaljenost \({\small 0}\).
- Ako su pravci paralelni, njihova je udaljenost jednaka udaljenosti bilo koje točke prvog pravca od njezine ortogonalne projekcije na drugi pravac.
- Udaljenost mimosmjernih pravaca jednaka je udaljenosti njihovih sjecišta sa zajedničkom normalom.
Naime, za svaka dva mimosmjerna pravca postoji jedinstveni pravac koji ih siječe i na svakog je okomit. Takav pravac nazivamo zajedničkom normalom mimosmjernih pravaca.
|
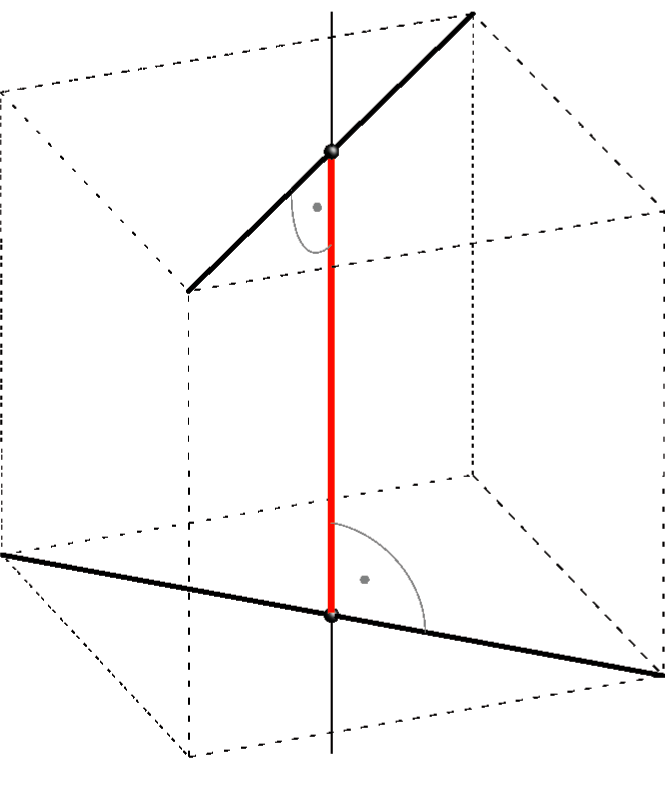
Slika 40: Udaljenost mimosmjernih pravaca.
|
Udaljenost između pravca i ravnine
- Ako se pravac i ravnina sijeku, njihova je udaljenost \({\small 0}\).
- Ako je pravac paralelan s ravninom, njihova je udaljenost jednaka udaljenosti bilo koje točke pravca od njezine ortogonalne projekcije na tu ravninu.
Udaljenost između dvije ravnine
- Ako se ravnine sijeku, njihova je udaljenost \({\small 0}\).
- Ako su ravnine paralelne, njihova je udaljenost jednaka udaljenosti bilo koje točke prve ravnine od njezine ortogonalne projekcije na drugu ravninu.
|
Sonja Gorjanc - GeomTeh3D - Razvojni projekt Sveučilišta u Zagrebu
|