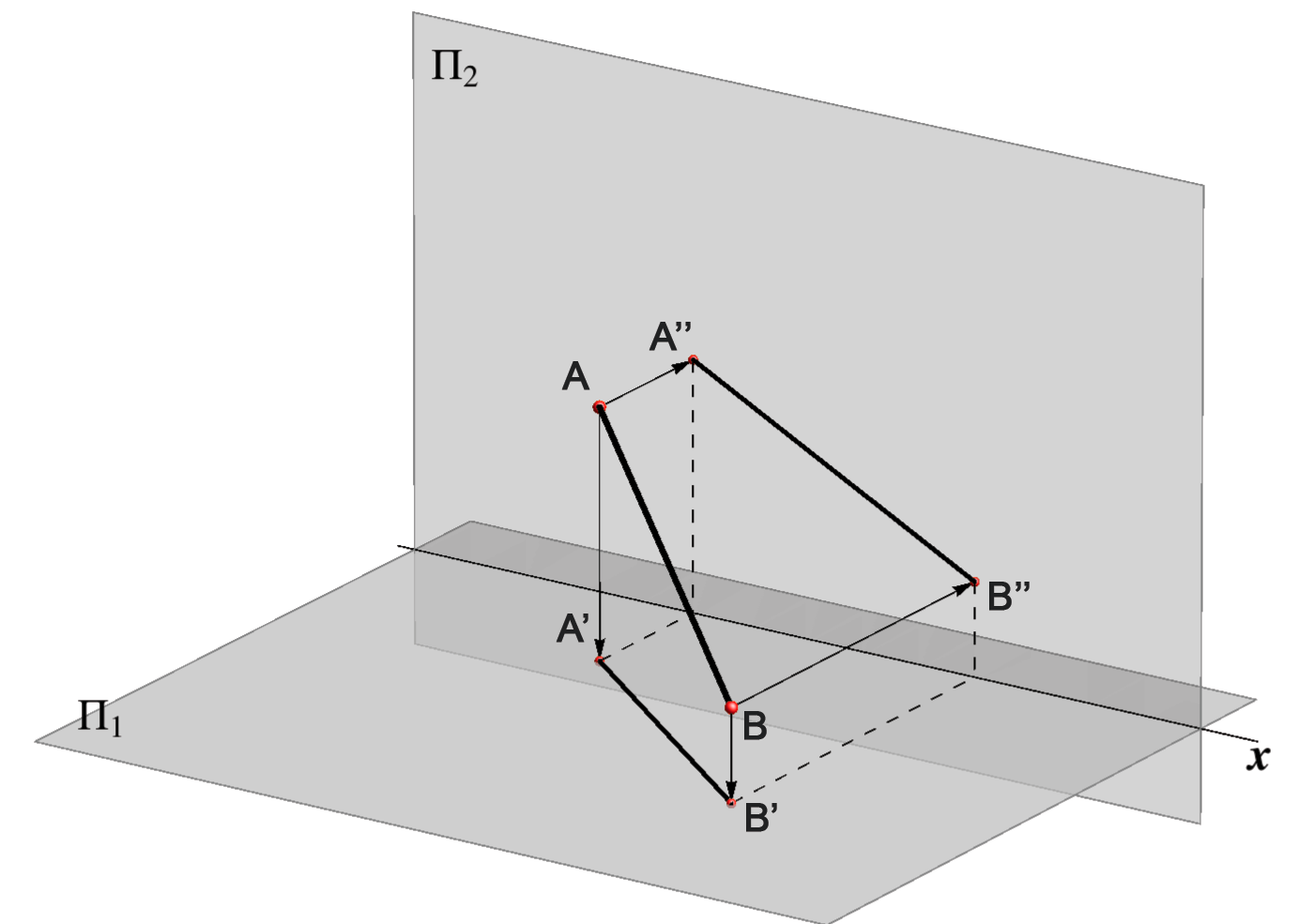
Slika 100
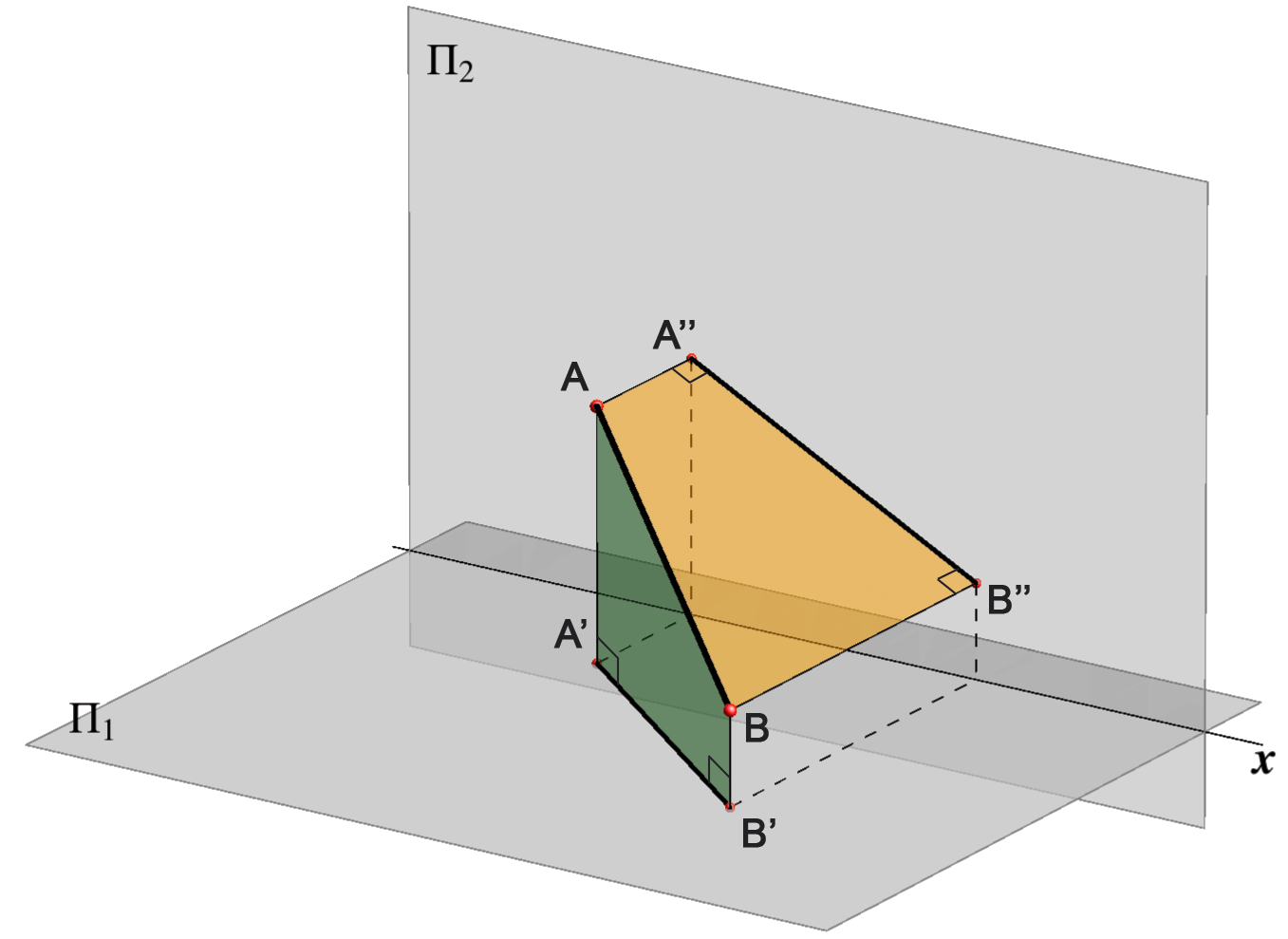
Slika 101
|

Slika 100 |

Slika 101 |
Određivanje duljine neke dužine \(\small\overline{AB}\) na temelju njezinih projekcija (\(\small\overline{A'B'}\),\(\small\overline{A''B''}\)) vrlo je važan metrički zadatak. Rješavamo ga na sljedeći način:
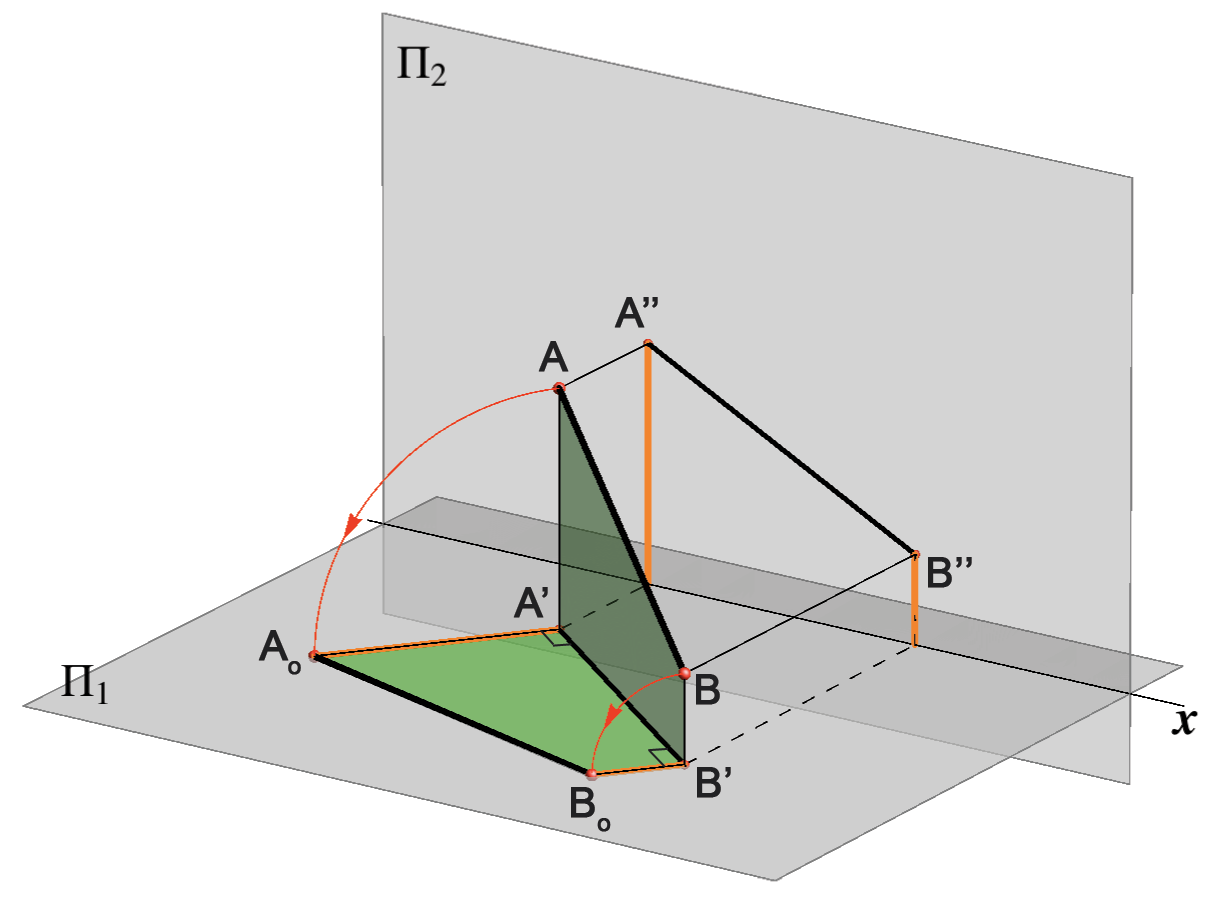
Taj konstruktivni postupak nazivamo prevaljivanjem u ravninu \(\small \Pi_1\). |
|
|
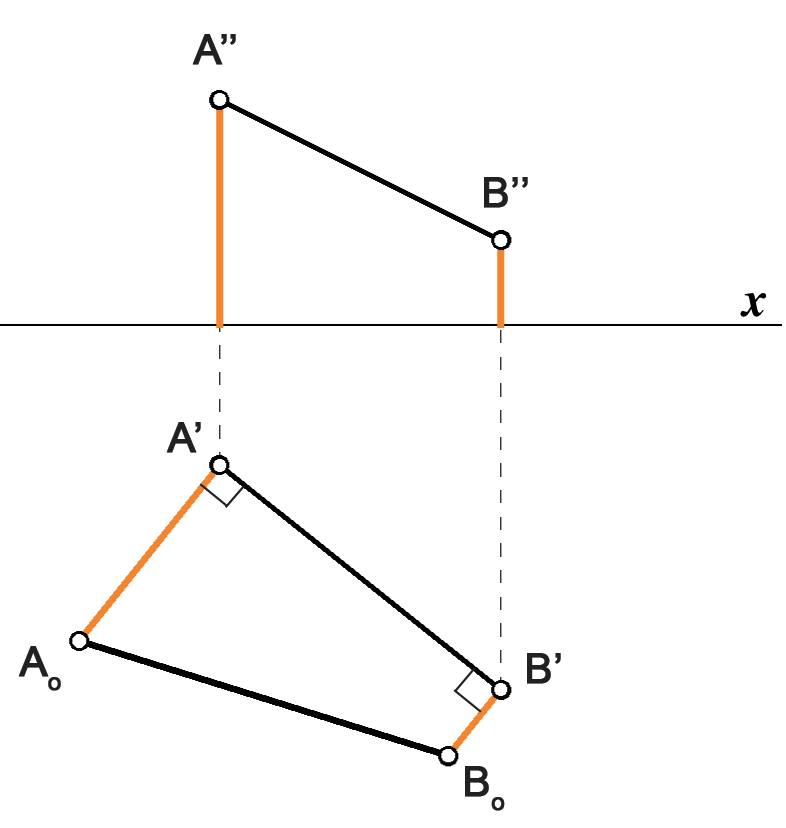
KONSTRUKCIJA (Interaktivna slika 37) |
| Slika 102 | Slika 103 |
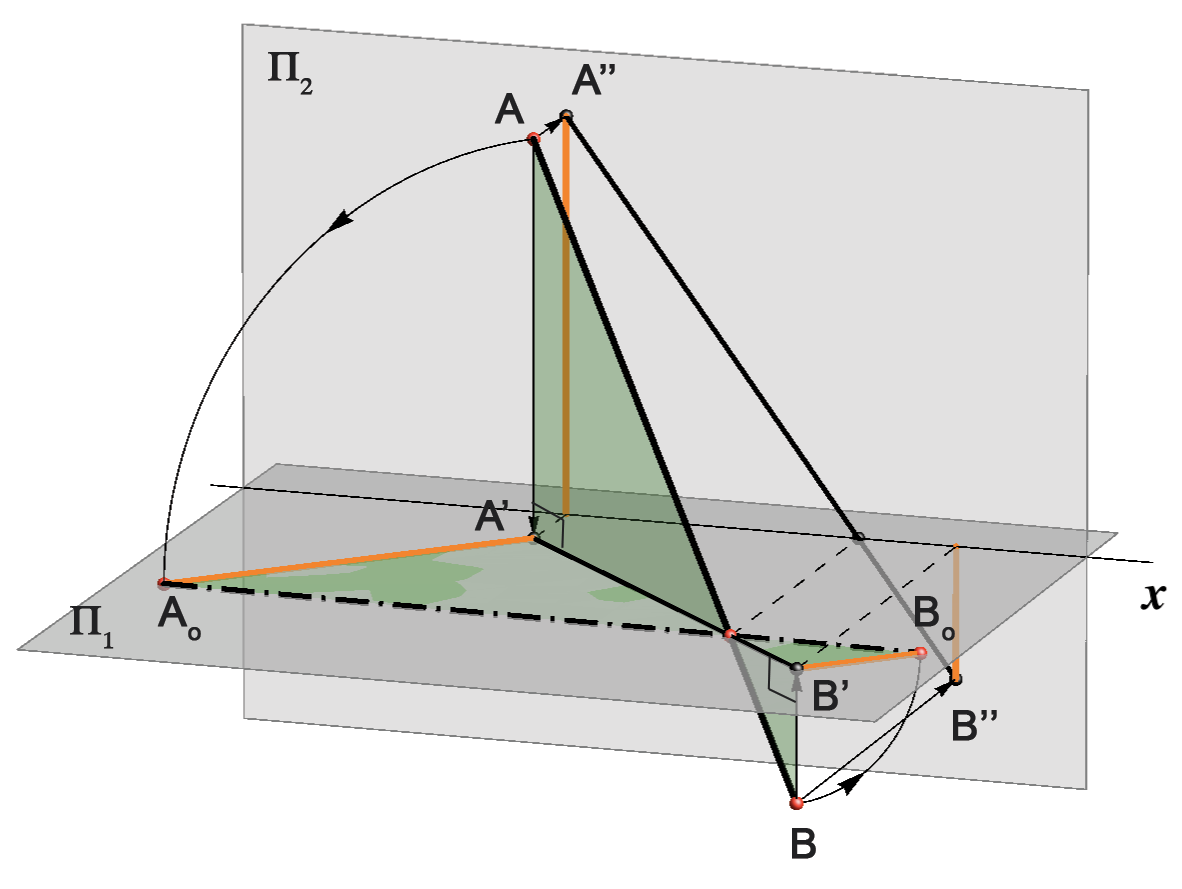
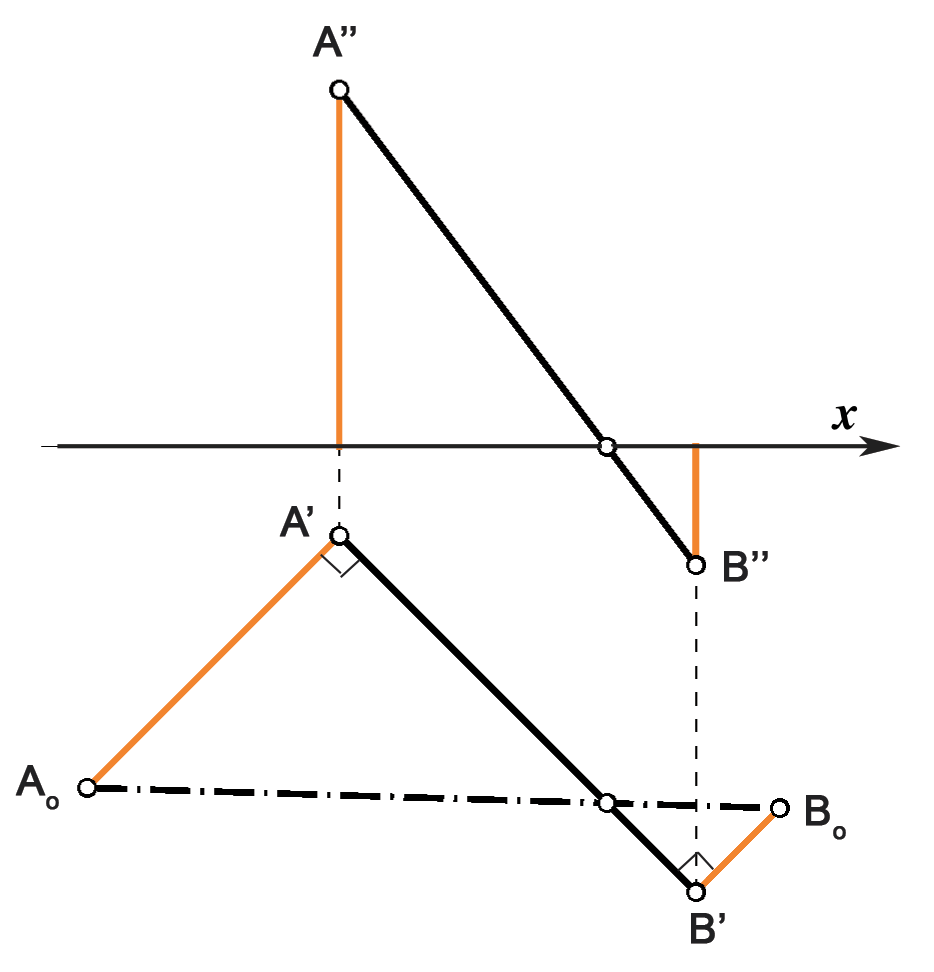
| Ukoliko su \(\small z\)-koordinate točaka \(\small A\) i \(\small B\) suprotnih predznaka, dužine čije su duljine jednake njihovim apsolutnim vrijednostima, nanosit ćemo prilikom prevaljivanja na suprotne strane okomica kroz \(\small A'\) i \(\small B'\) (slika 104). Stoga ćemo u prevaljenom položaju umjesto pravokutnog trapeza dobiti dva pravokutna trokuta (slika 105). |
|
|
| Slika 104 | Slika 105 |
|
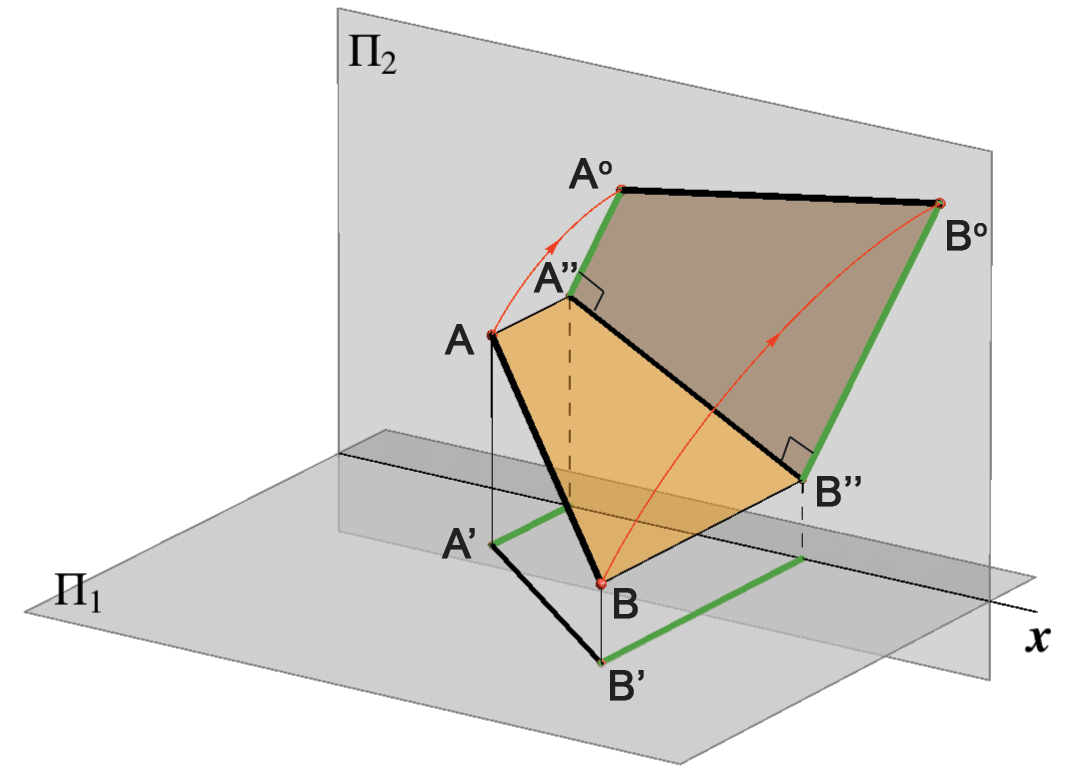
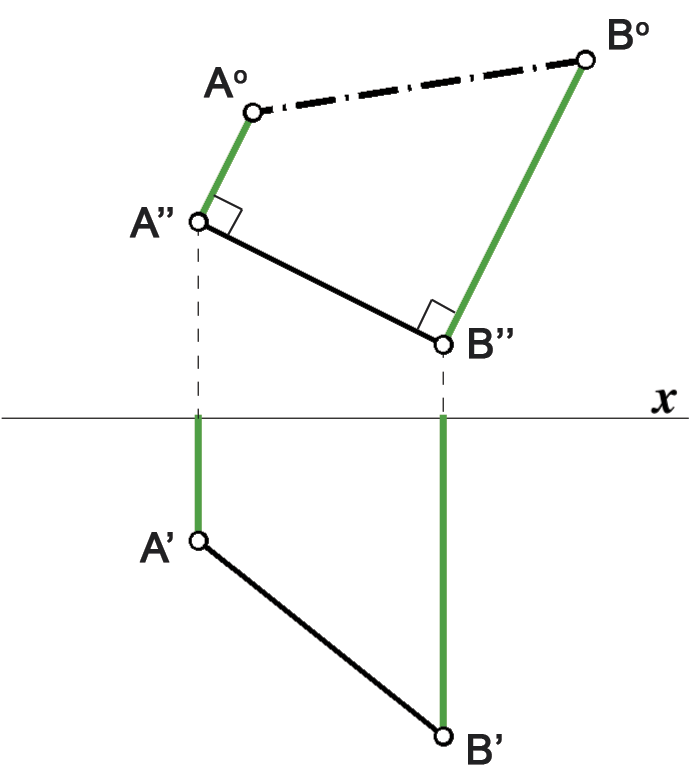
Prevaljivanje u ravninu \(\small \Pi_2\) je postupak koji je analogan onom pri prevaljivanju u \(\small \Pi_1\). Pritom ćemo pravokutni trapez \(\small ABB''A''\) rotirati oko pravca \(\small A''B''\), za kut od \(\small 90^\circ\) u ravninu \(\small \Pi_2\). Duljine paralelnih stranica pravokutnoga trapeza jednake su apsolutnim vrijednostima \(\small y\)-koordinata točaka \(\small A\) i \(\small B\), a rotirane položaje označavat ćemo \(\small A^\circ\) i \(\small B^\circ\). Vidi slike
106 i 107.
Isto kao i pri postupku prevaljivanja u \(\small \Pi_1\), ako su \(\small y\)-koordinate točaka \(\small A\) i \(\small B\) suprotnih predznaka, u rotiranom ćemo položaju umjesto pravokutnog trapeza konstruirati dva pravokutna trokuta. |
|
|
KONSTRUKCIJA (Interaktivna slika 38) |
| Slika 106 | Slika 107 |
Slučajevi kada se dužina projicira u pravoj veličini
|
 |
 |
 |
|
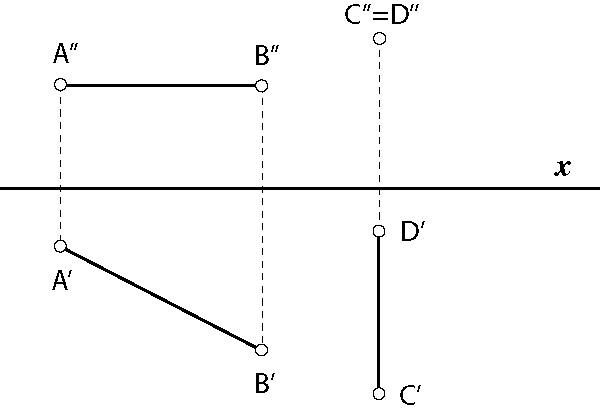
Slika 108: Dužine \(\small \overline{AB}\) i \(\small\overline{CD}\) paralelne su s \(\small \Pi_1\), u tlocrtu se projiciraju u pravoj veličini. |
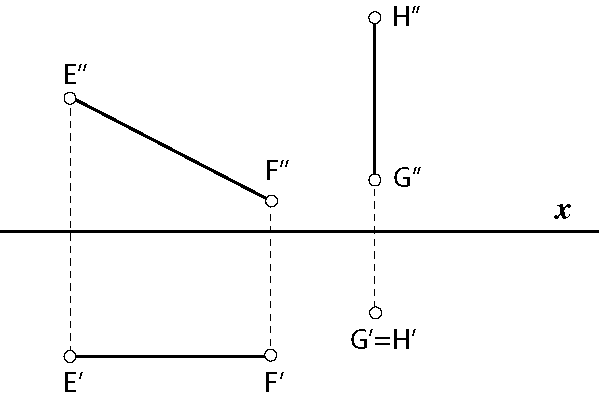
Slika 109: Dužine \(\small\overline{EF}\) i \(\small\overline{GH}\) paralelne su s \(\small \Pi_2\), |
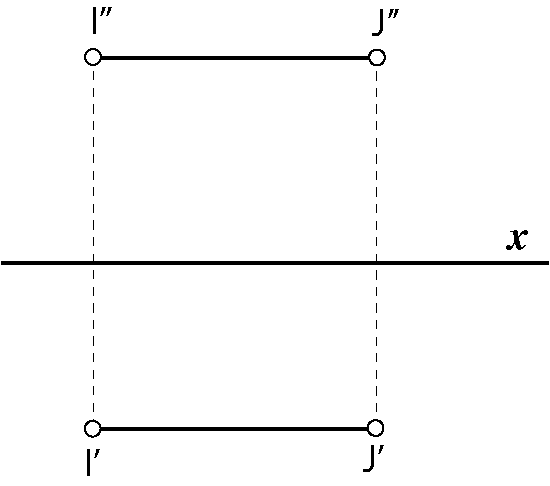
Slika 110: Dužina \(\small\overline{IJ}\) paralelna je s osi \(\small x\), projicira se u pravoj veličini u obje projekcije. |
Sonja Gorjanc - GeomTeh3D - Razvojni projekt Sveučilišta u Zagrebu