Intersections with a sphere

Every plane intersection of a sphere is a circle. To construct the points of the inetersection curve of a sphere and another surface, we choose a system of planes that cutt the other surface in the simplest possible curves.
When we intersect a sphere with a surface of revolution, we choose a system of planes that cutt the surface of revolution in circles.

Intersection of two spheres

A sphere intersects the plane at infinity in a conic, which is called the absolute conic of the space.

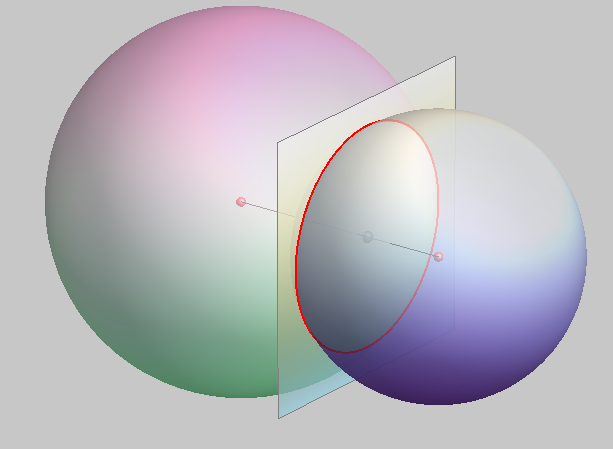
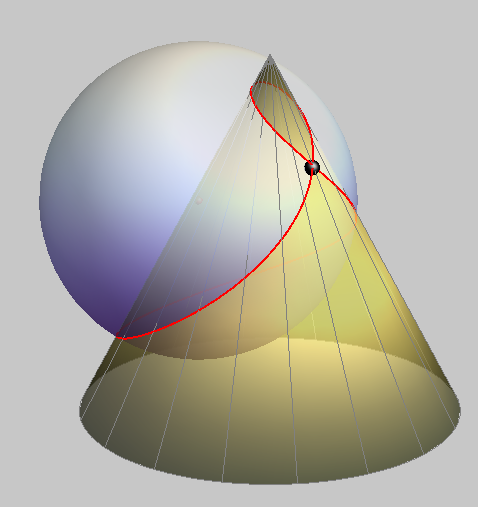
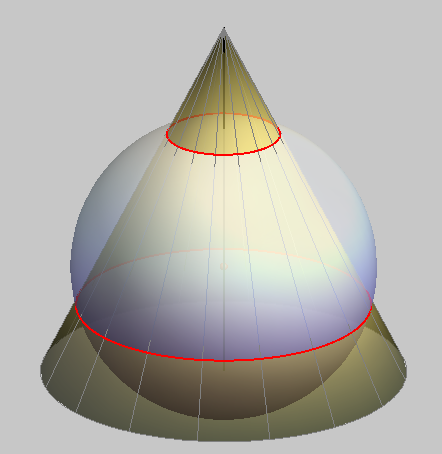
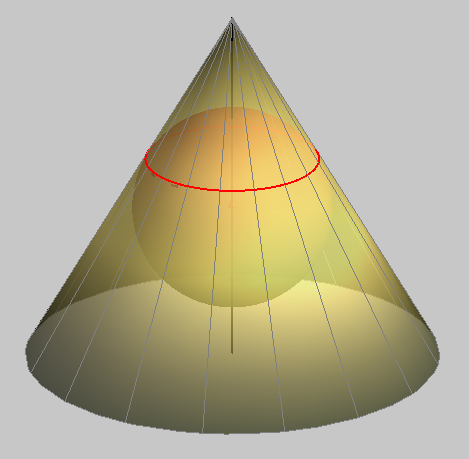
The intersection curve of two sphere always degenerates into the absolute conic and a circle.

Therefore, the real intersection of two spheres is a circle.
The plane determined by this circle is perpendicular to the line connecting the centers of the spheres and this line passes through the center of this circle.

Intersection of a sphere and a cylinder

The intersection curve of a sphere and a cylinder is a space curve of the 4th order.
This curve can be a one-branch curve in the case of partial intersection, a two-branch curve in the case of complete intersection or a curve with one double point if the surfaces have a common tangent plane.


PARTIAL INTERSECTION - a one-branch curve
COMPLETE INTERSECTION - a two-branch curve
an intersection curve with ONE DOUBLE POINT


If the center of the sphere lies on the axis of the cylinder of revolution, then the intersection curve degenerates into two circles.
When the diameter of the sphere is the same as the diameter of the base circle of the cylinder, the two circles coincide and the two surfaces have the same tangent plane at every point of this circle.


two circles

one double circle


Intersection of a sphere and a cone

The intersection curve of a sphere and a cone is a space curve of the 4th order.
This curve can be a one-branch curve in the case of partial intersection, a two-branch curve in the case of complete intersection or a curve with one double point..
The intersection curve has a double point in two cases - if the surfaces have a common tangent plane in a regular point or when the sphere passes through the double point of the cone, its vertex.



PARTIAL INTERSECTION - a one-branch curve

COMPLETE INTERSECTION - a two-branch curve




an intersection curve with ONE DOUBLE POINT
Surfaces have a common tangent plane.

an intersection curve with ONE DOUBLE POINT
The sphere passes through the vertex of the cone.


If the center of the sphere lies on the axis of the cone of revolution, then the intersection curve of these surfaces degenerates into two circles.
These two circles can coincide and then the surfaces have the same tangent plane in every point of the circle.



two circles


one double circle



Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb