\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=2cz\) (eliptički u užem smilslu)
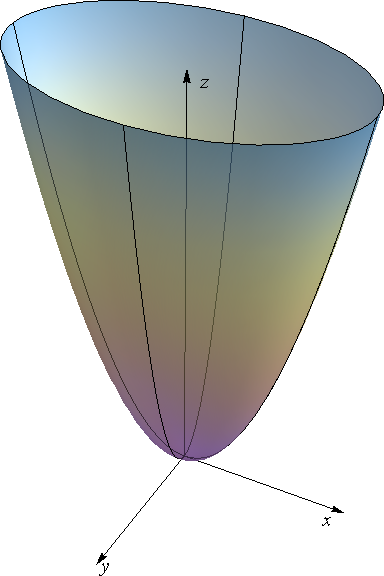
Nastaje rotacijom parabole oko njezine osi (slika 21 i animacija 11).
|
|
|
Osnovna podjela paraboloida je na eliptičke (koji kao podtip sadrže rotacijske paraboloide) i hiperboličke. Sve točke na eliptičkim paraboloidima su eliptičke, a one na hiperboličkim su hiperboličke. Realni presjeci eliptičkih paraboloida mogu biti elipse, kružnice i parabole, a presjeci hiperboličkih paraboloida mogu biti parabole, hiperbole i dva realna pravca. Beskonačno daleka ravnina prostora siječe paraboloide po dva različita pravca. Ako su ti pravci imaginarni tada je paraboloid eliptički, a ako su realni tada je hiperbolički.
|
|
1. eliptički paraboloidi
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=2cz\) (eliptički u užem smilslu)
|
\(\frac{x^2+y^2}{a^2}=2cz\) (rotacijski)
Nastaje rotacijom parabole oko njezine osi (slika 21 i animacija 11).
|
| Slika 20: Eliptički paraboloid | Slika 21 | Animacija 11: Rotacijski paraboloid |
|
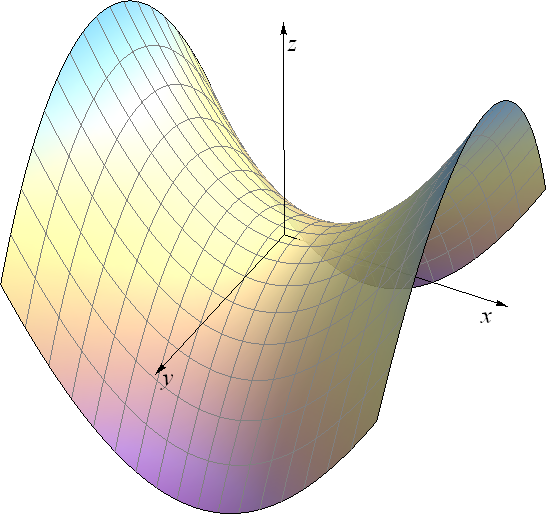
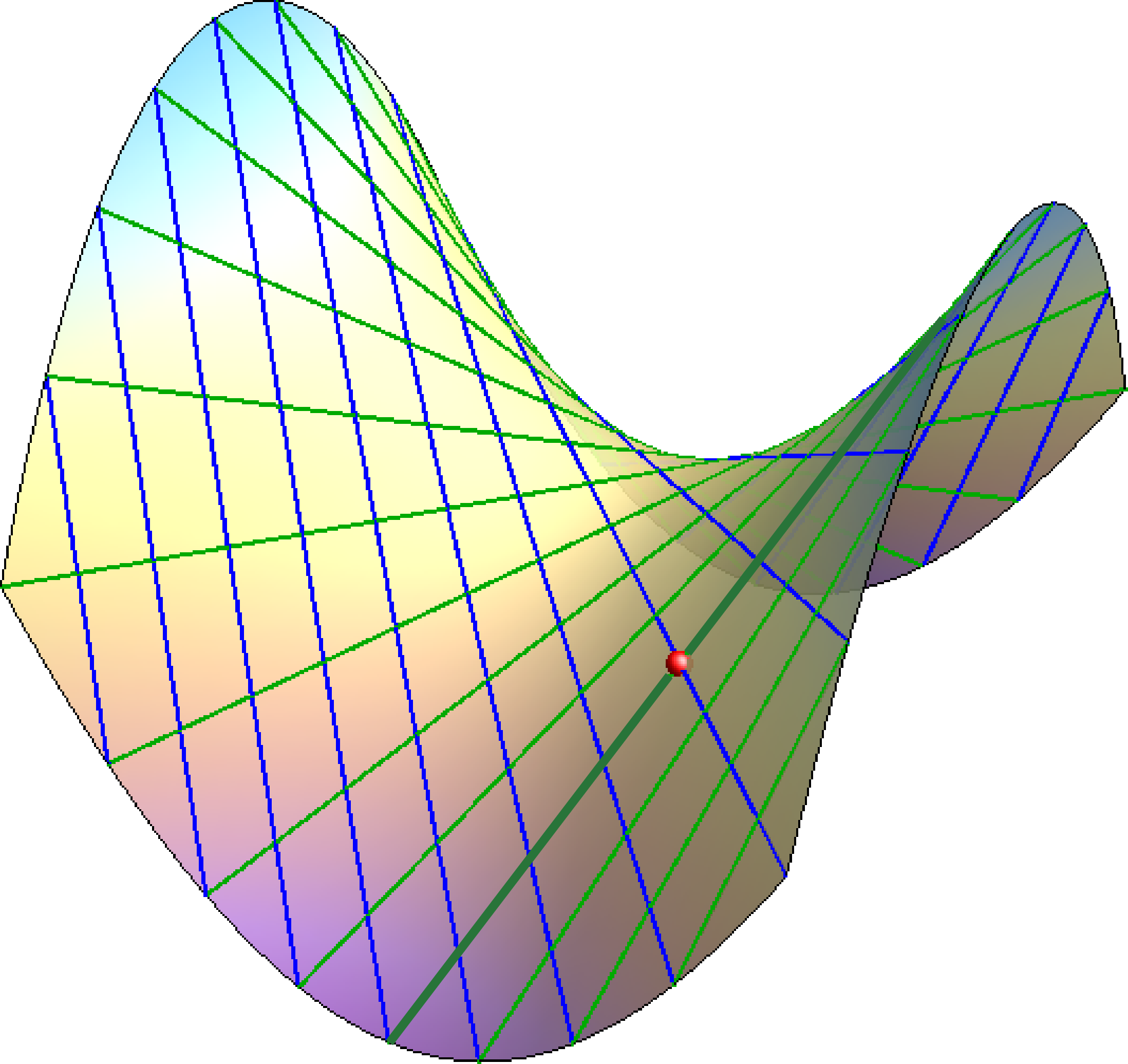
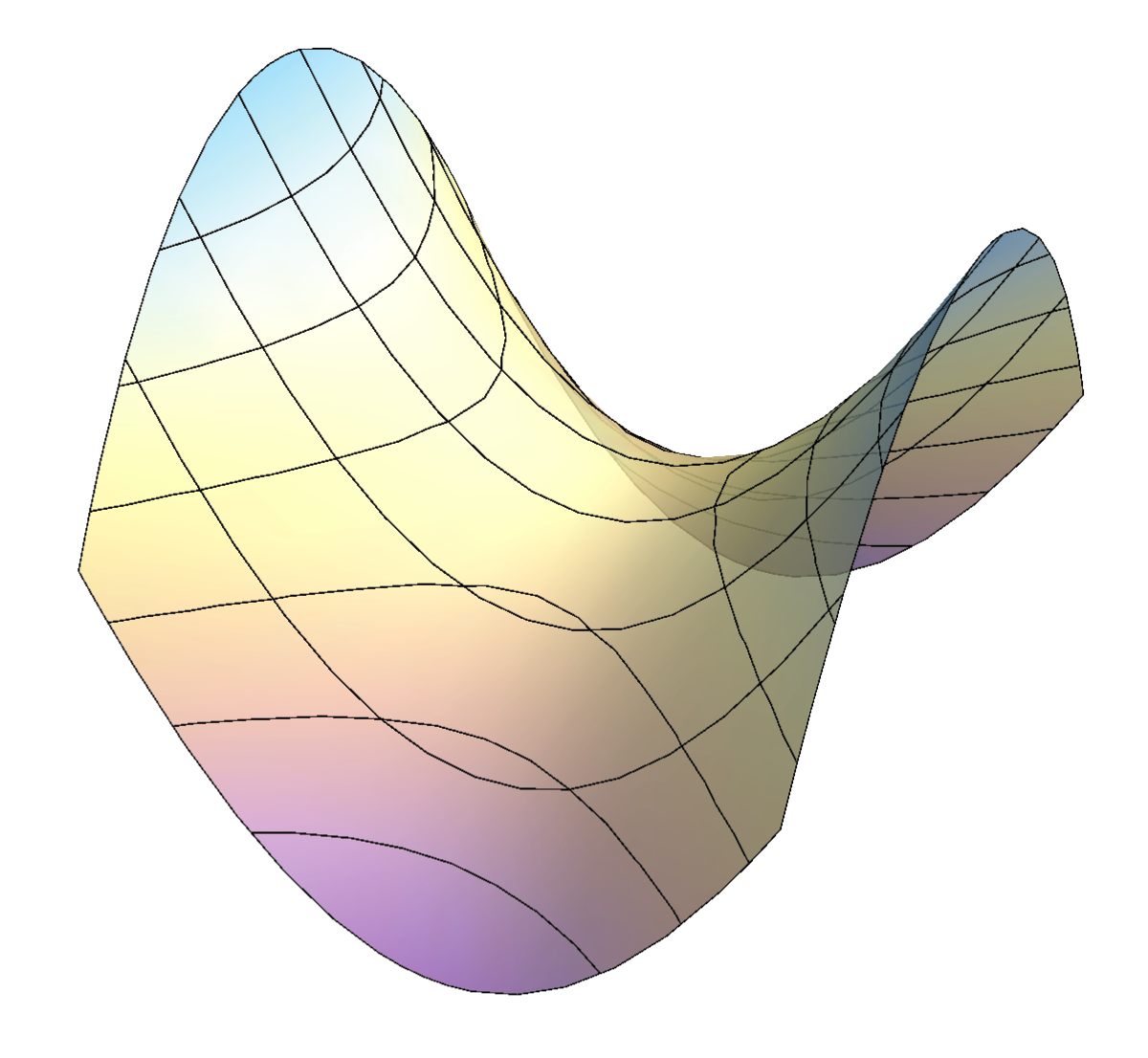
2. hiperbolički paraboloid (hipar)
\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=2cz\) Hipar je, kao i jednokrilni hiperboloid, pravčasta ploha s dva sistema izvodnica. Svakom njegovom točkom prolaze dvije izvodnice - po jedna iz svakog sistema (slika aa). Za razliku od jednokrilnog hiperboloida svaki od ta dva sistema ima jednu izvodnicu u beskonačnosti, to su realni pravci po kojima beskonačno daleka ravnina siječe hipar. Posljedica toga je činjenica da realni presjeci hipara ne mogu biti elipse, od pravih se konika na tim plohama pojavljuju samo hiperbole i parabole. Zašto? |
|
|
|
| Slika 22: | Slika 23: | Slika 24: |
Sonja Gorjanc - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu