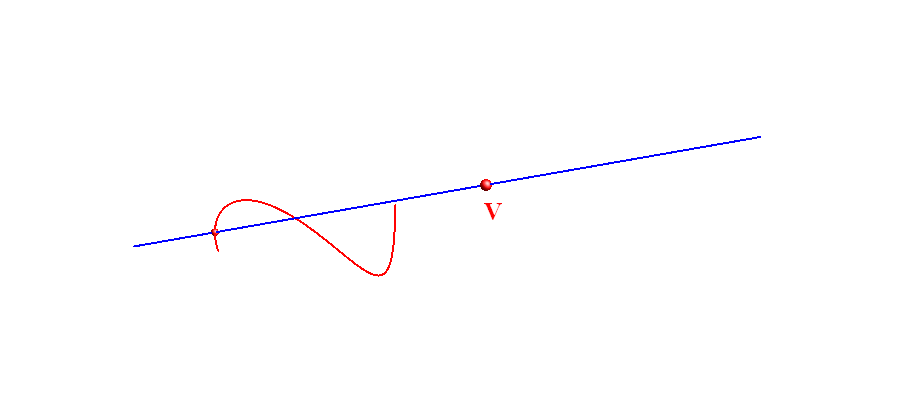
Animacija 3: Stožasta ploha
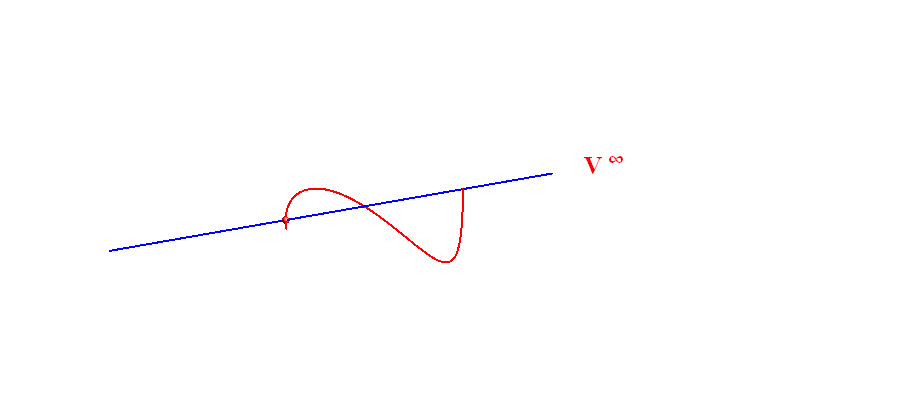
Animacija 4: Valjkasta ploha
|
Stožac možemo definirati kao skup pravaca koji su spojnice točaka neke prostorne ili ravninske krivulje s jednom točkom u konačnosti, pri čemu ta točka ne leži u ravnini te krivulje (ako je krivulja ravninska). Istaknuta točka u konačnosti je vrh stošca, a spojnice tog vrha s točkama zadane krivulje su izvodnice stošca. Vidi animaciju 3.
Valjak definiramo kao skup pravaca koji spajaju točke neke prostorne ili ravninske krivulje s jednom beskonačno dalekom točkom prostora, a ona ne leži u ravnini te krivulje (ako je krivulja ravninska). Sve takve spojnice su međusobno paralelne i nazivamo ih izvodnicama valjka. Njhovo beskonačno daleko sjecište nazivamo vrhom valjka. Vidi animaciju 4. Stožac i valjak su pravčaste plohe. |

Animacija 3: Stožasta ploha |

Animacija 4: Valjkasta ploha |
|
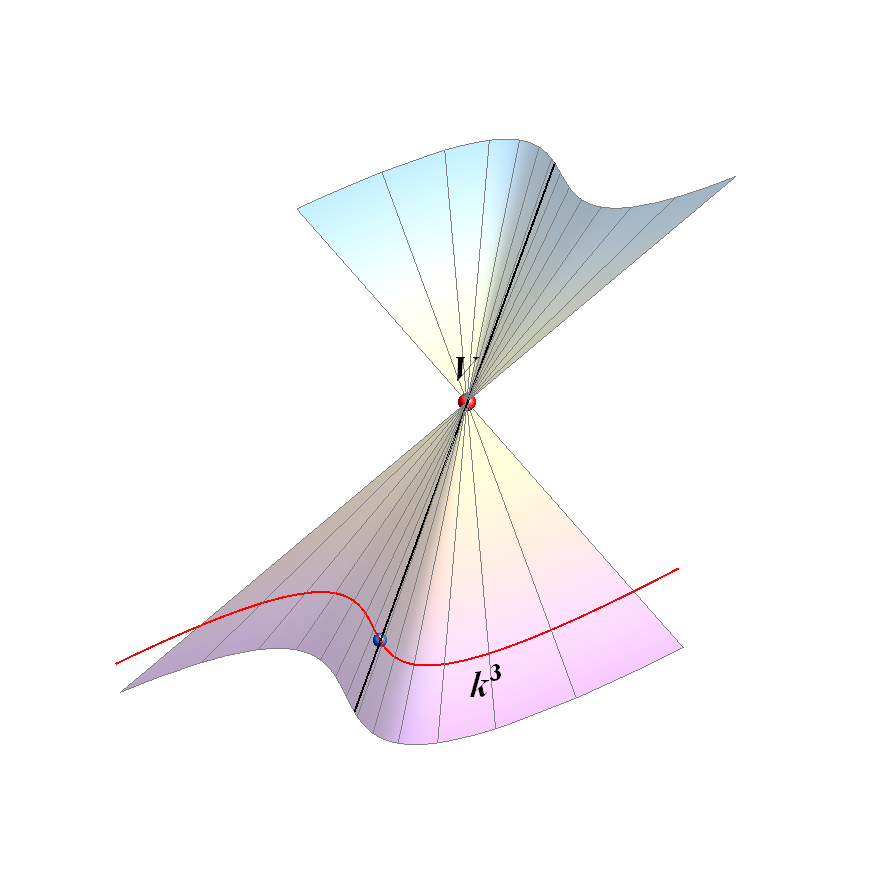
Slika xy: Stožac 3. stupnja |
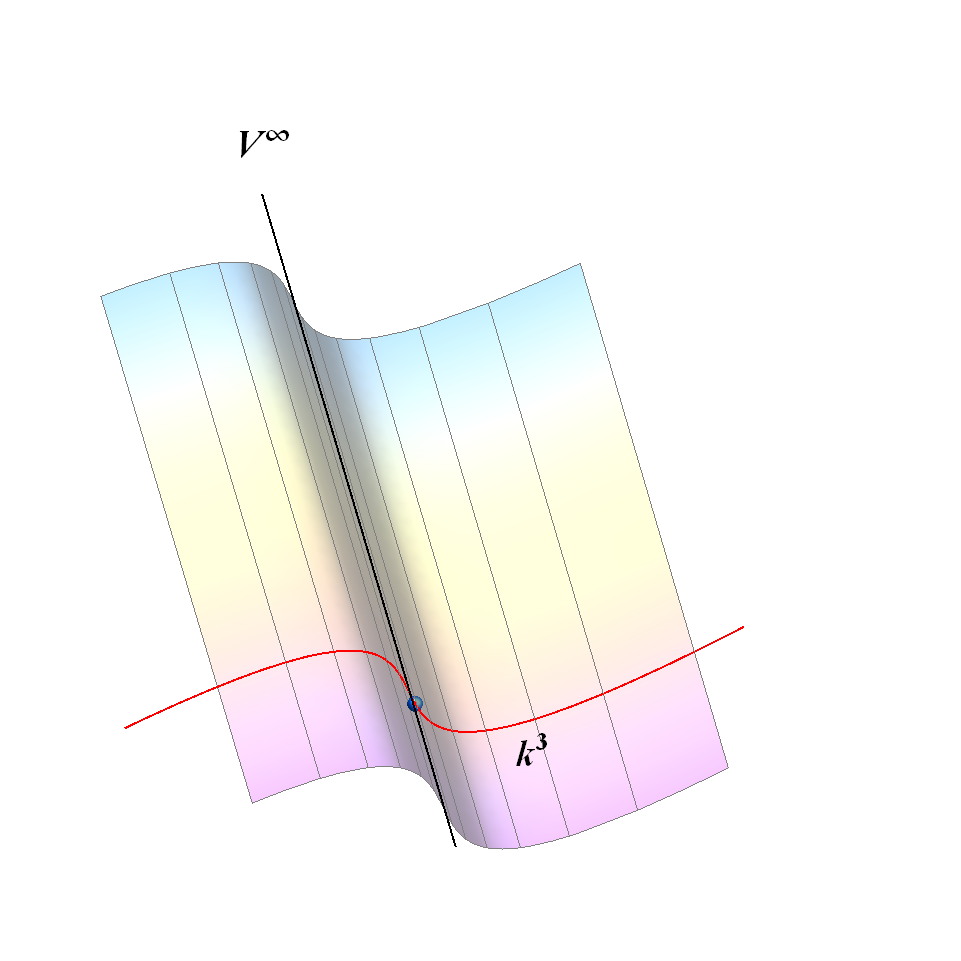
Slika xy: Valjak 3. stupnja |
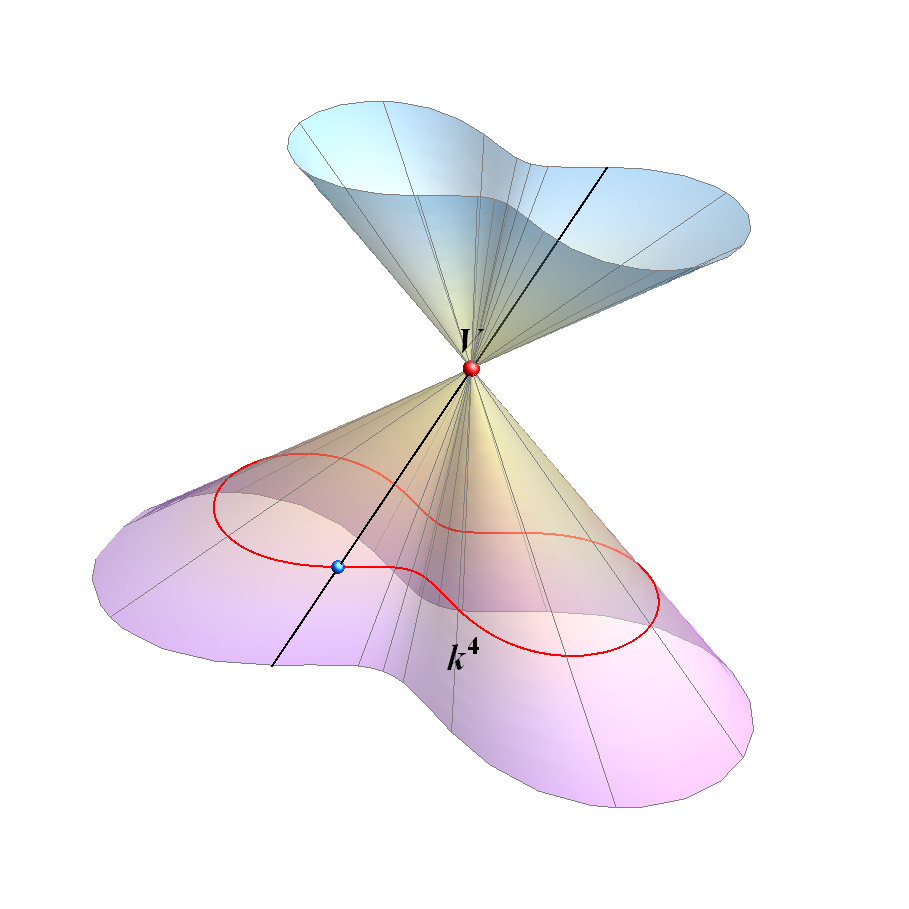
Slika xy: Stožac 4. stupnja |
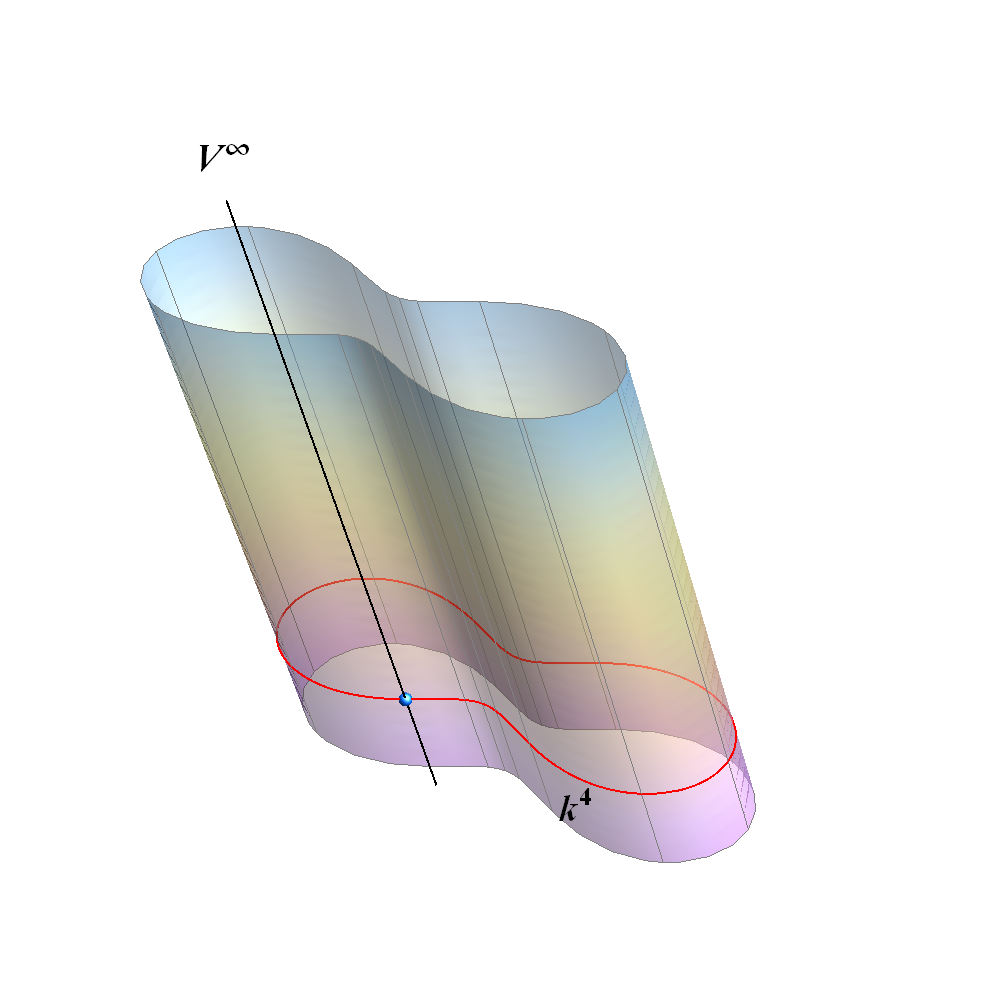
Slika xy: Valjak 4. stupnja |
| * Izraze stožac i valjak upotrebljavamo dvoznačno. Nekada oni označavaju tijela koja se sastoje od jedne (stožac) ili dvije (valjak) osnovke ili baze te plašta koji je dio zakrivljene plohe. Te zakrivljene neograničene plohe mogli bismo nazivati stožastim i valjkastim plohama, ali je u našem jeziku uobičajeno i za njih upotrebljavati izraze stožac i valjak. |
Sonja Gorjanc - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu