Kotirana projekcija

U poglavlju Mongeova metoda mogli smo uočiti da je položaj točke u prostoru jednoznačno određen s njezine dvije ortogonalne projekcije (primjerice tlocrtom i nacrtom). Međutim, u primjeni su česte situacije kod kojih uporaba dviju projekcija nije moguća ili je neprikladna za konstrukciju. U tim slučajevima možemo promatrati ortogonalnu projekciju na samo jednu ravninu, dok podatak o udaljenosti točke od te ravnine (za što je služila druga ortogonalna projekcija) izražavamo brojem, odnosno kotom. Takvu projekciju nazivamo kotiranom projekcijom.

U našim ćemo primjerima obraditi dijelove osnovnih zadataka koji se odnose na neke primjene kotirane projekcije u tehnici (prometnice na terenu i sloj). Standardna hrvatska terminologija nacrtne geometrije, koju u ovom udžbeniku koristimo, u pojedinim tehničkim područjima zamjenjuje se stručnim nazivljem. Stoga ćemo mjestimice istaknuti termine koji se koriste na smjeru Prometnice na Građevinskom fakultetu u Zagrebu.


Osnovno o kotiranoj projekciji

Kotirana projekcija je ortogonalna projekcija na jednu ravnini pri kojoj su podaci o udaljenosti geometrijskih objekata od ravnine projekcije dani brojevima koje nazivamo kotama.

Uobičajeno je za ravninu projekcije odabrati horizontalnu ravninu (ravninu tlocrta) u kojoj su kote svih točaka jednake 0.

Ravnine paralelne s ravninom projekcije nazivamo nivo-ravninama\(^*\). Točke u tim ravninama imaju iste kote, jer su jednako udaljene od ravnine projekcije.

Ravnine u kojima su kote točaka cijeli brojevi nazivamo glavnim nivo-ravninama.

\(^*\) Prometnice GFZ: nivo-ravnina \(\rightarrow\) sravnjujuća ravnina.




Slika 2.152: Glavne nivo-ravnine.

Mjerilo

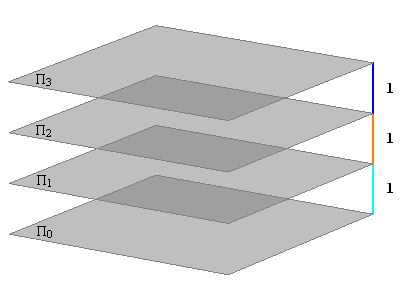
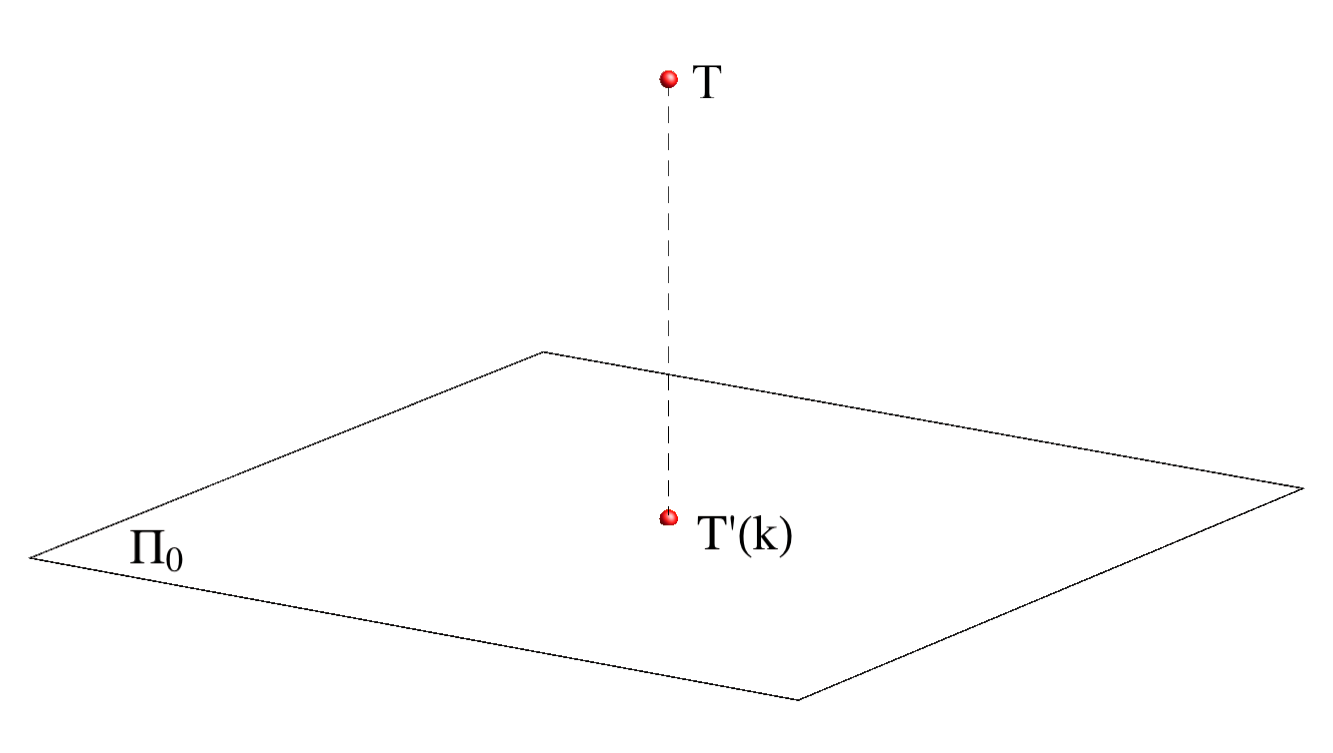
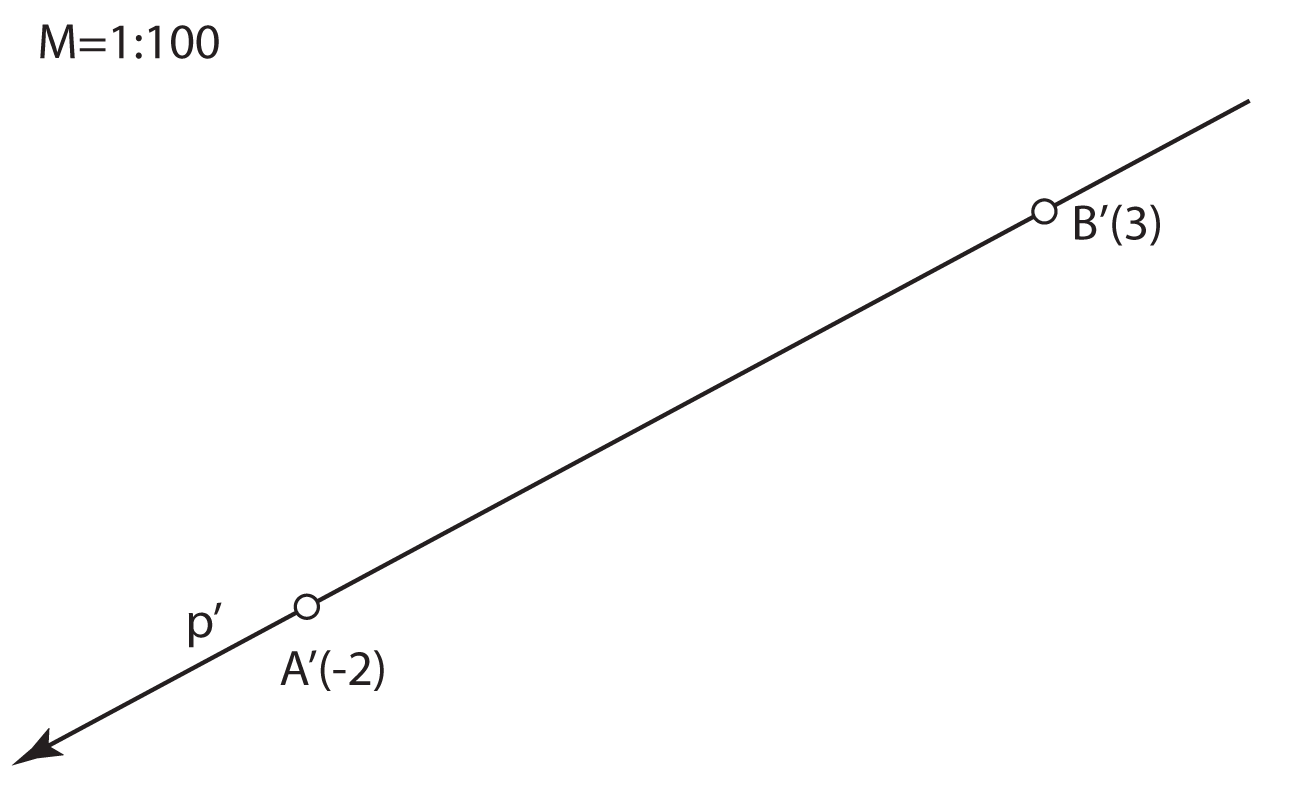
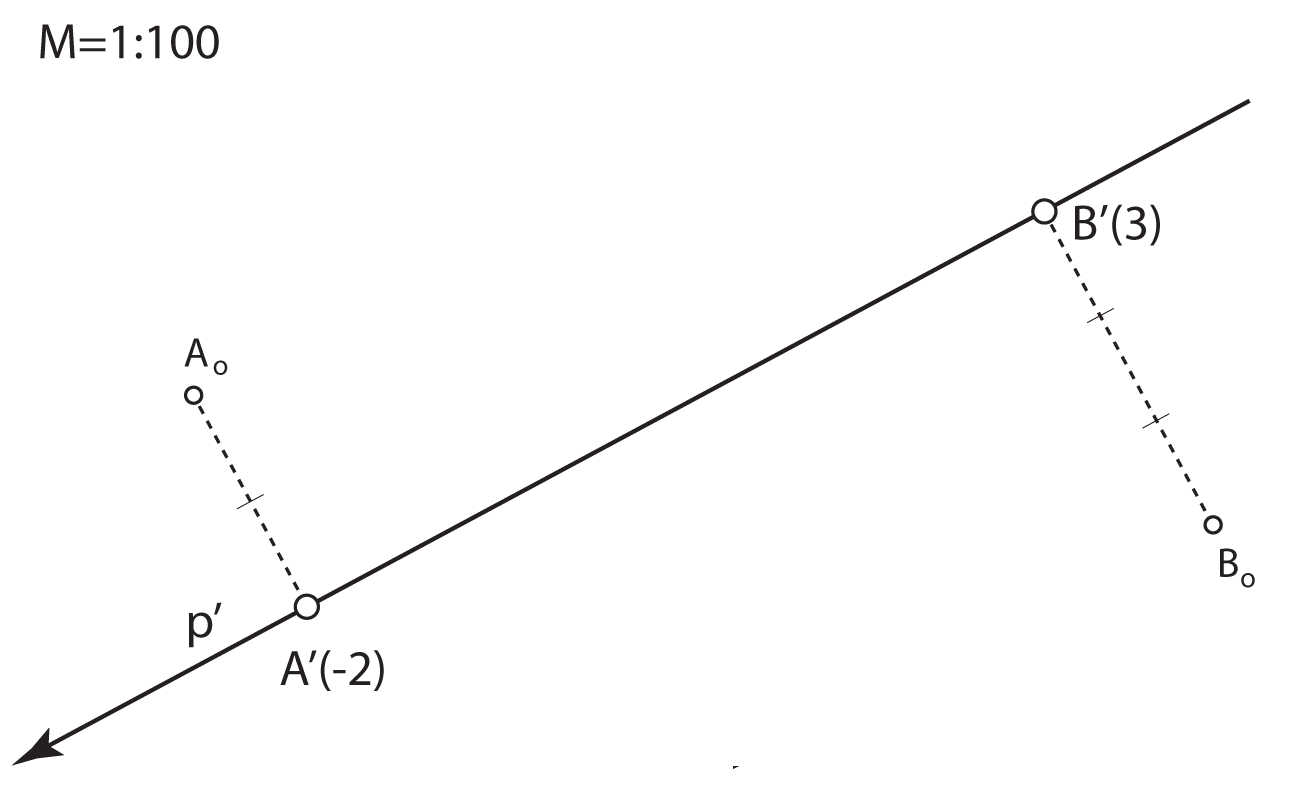
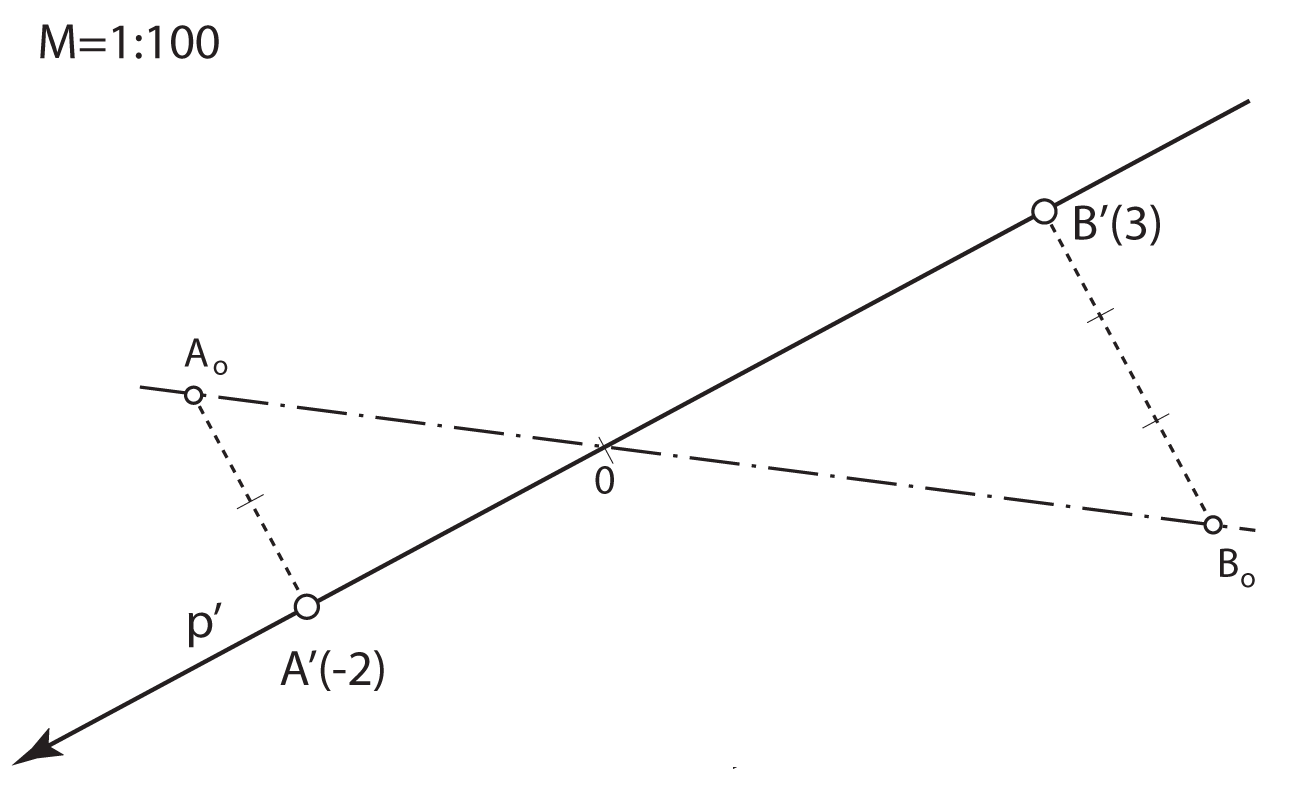
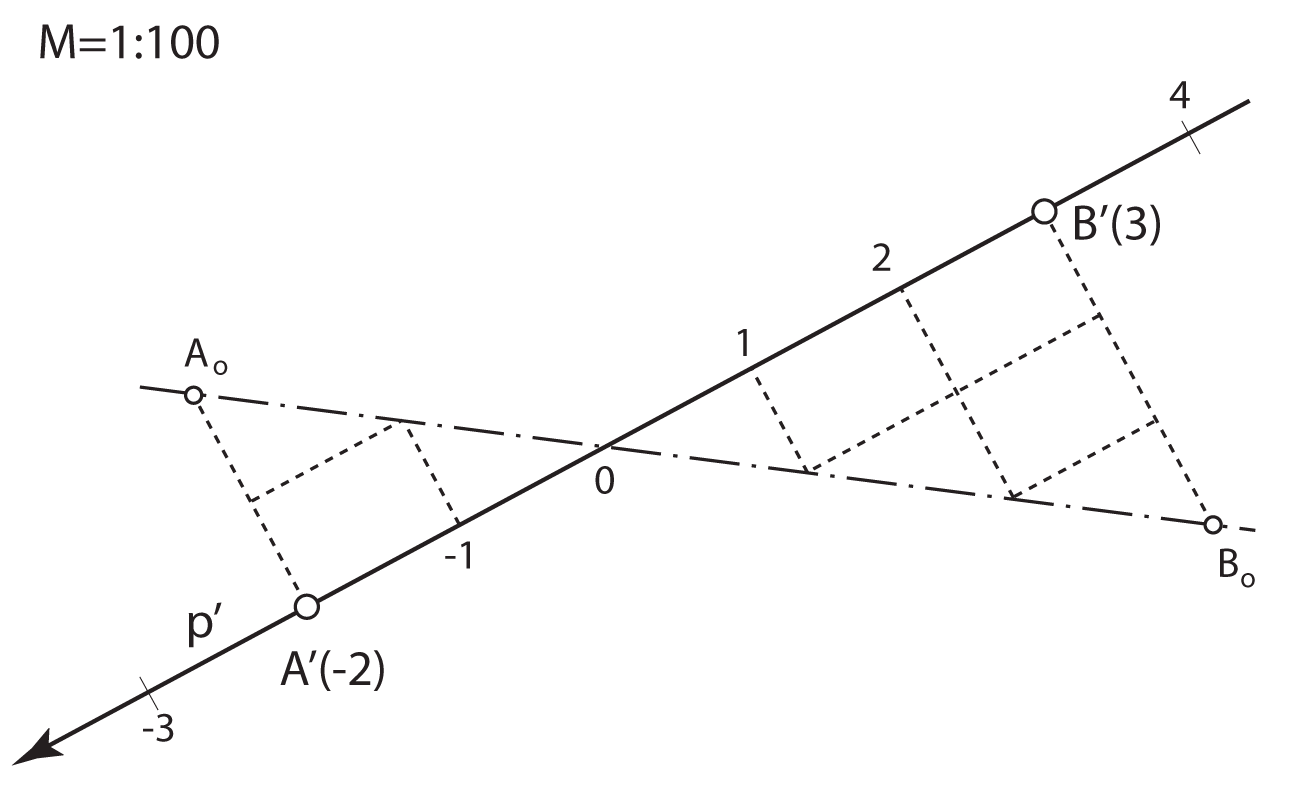
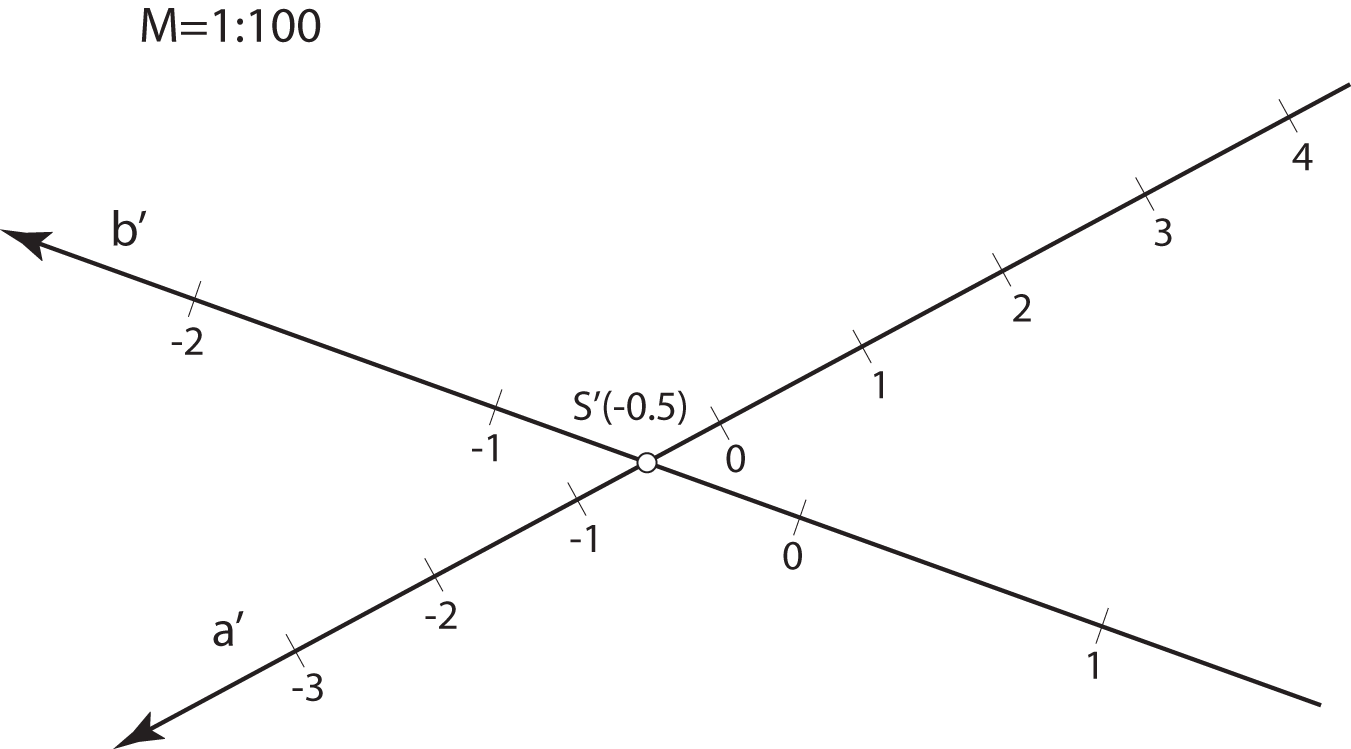
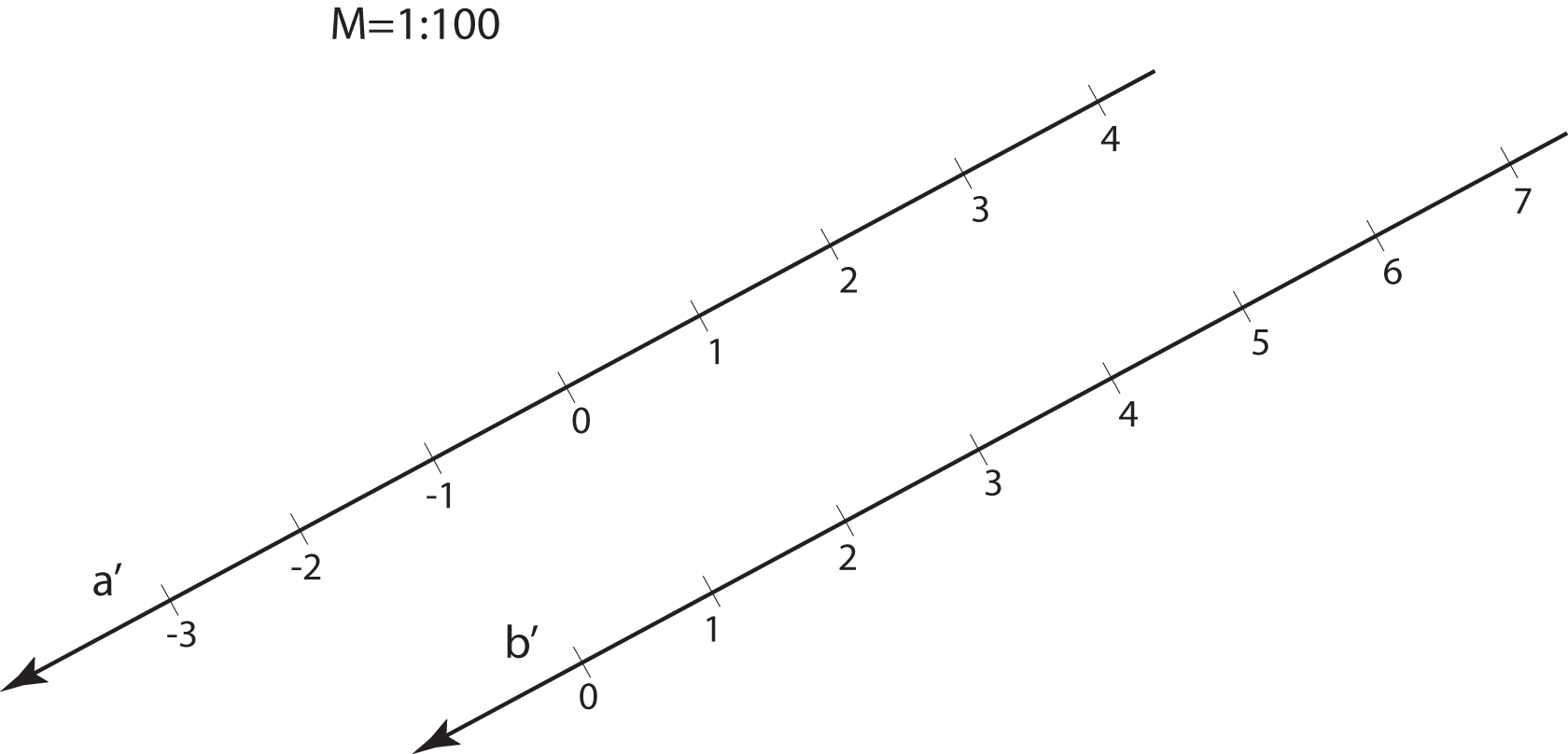
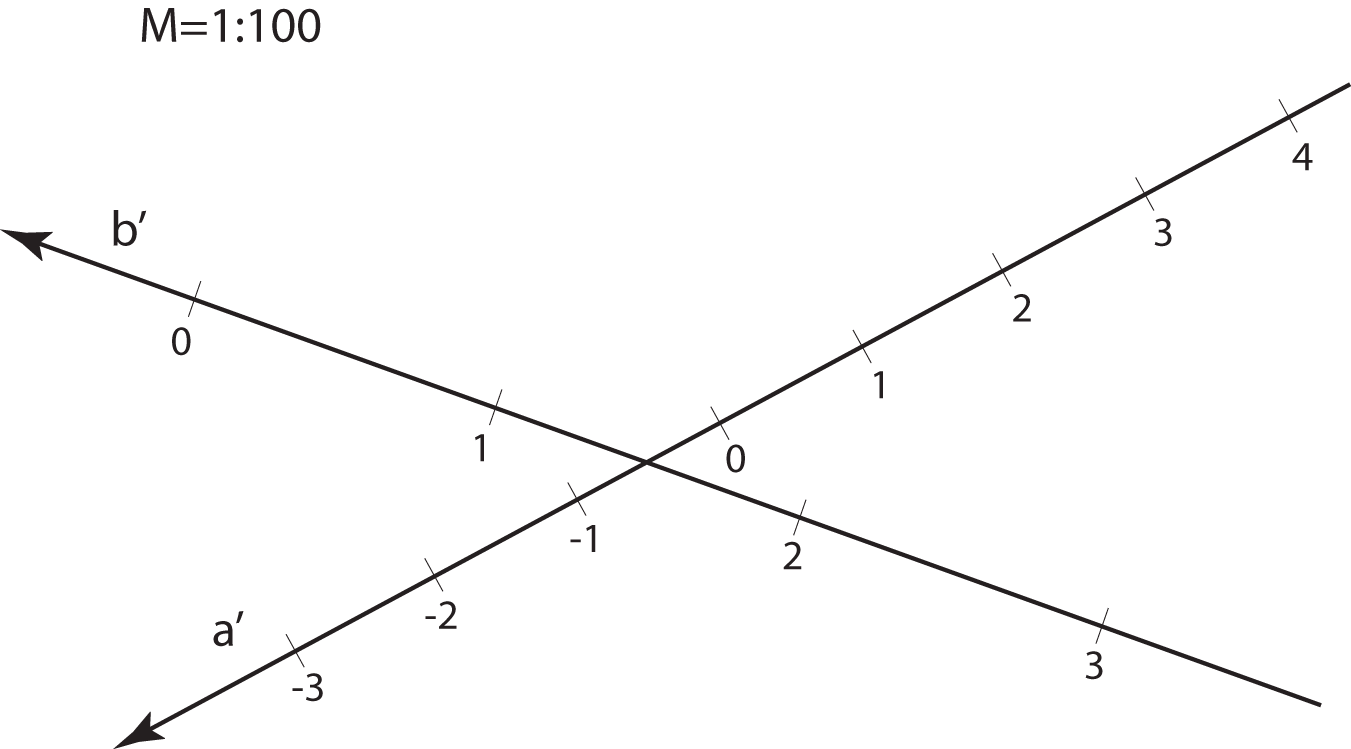
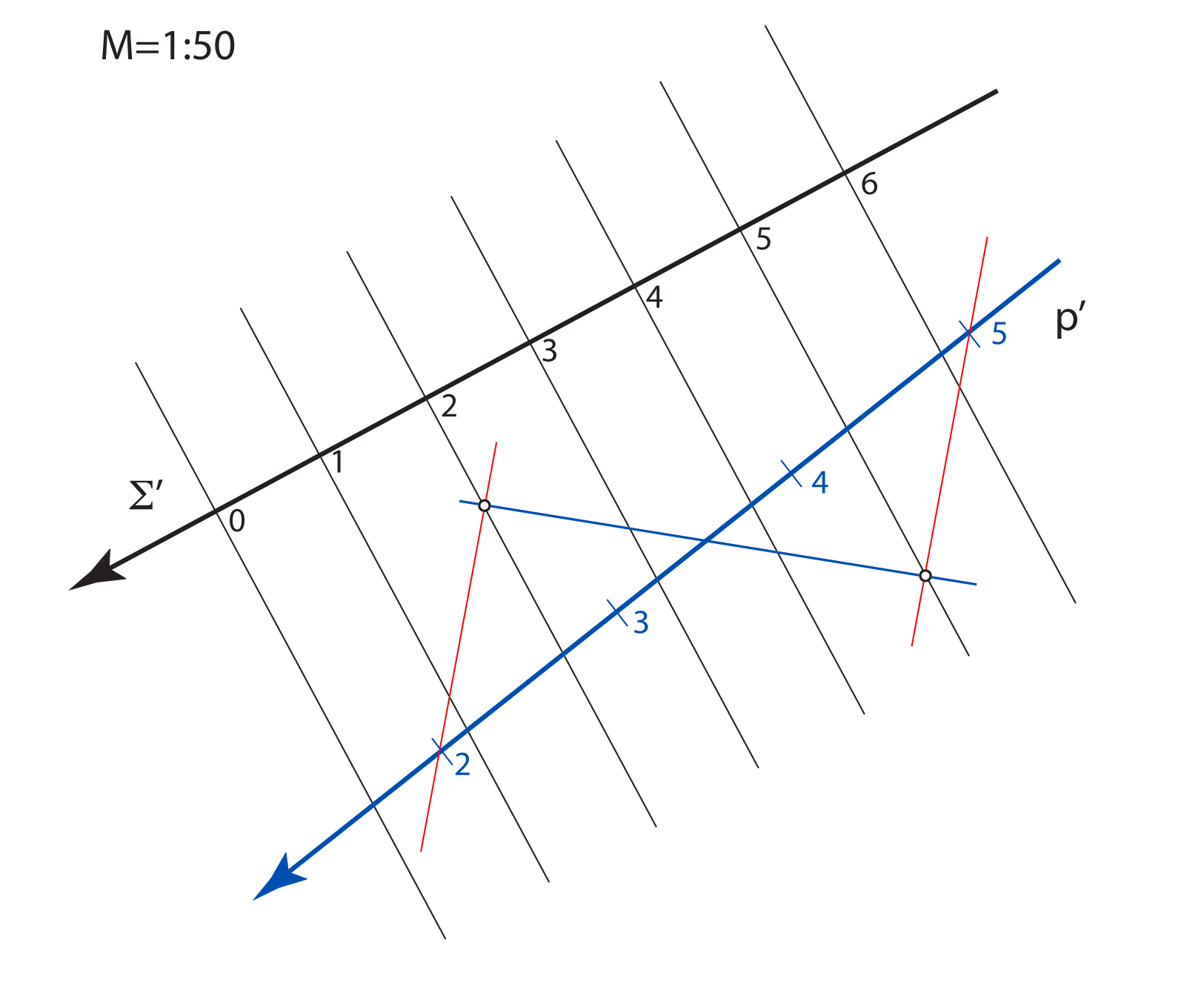
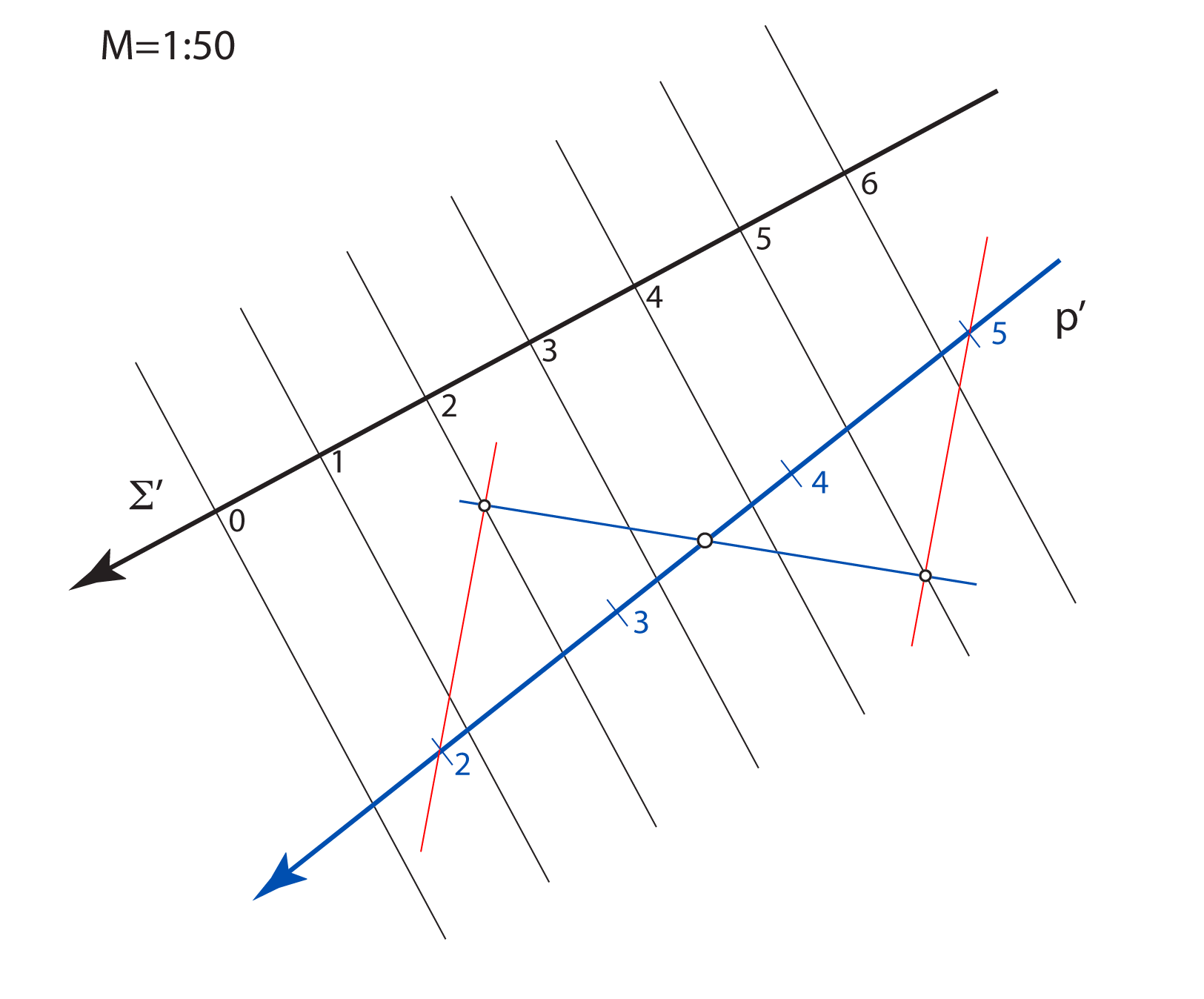
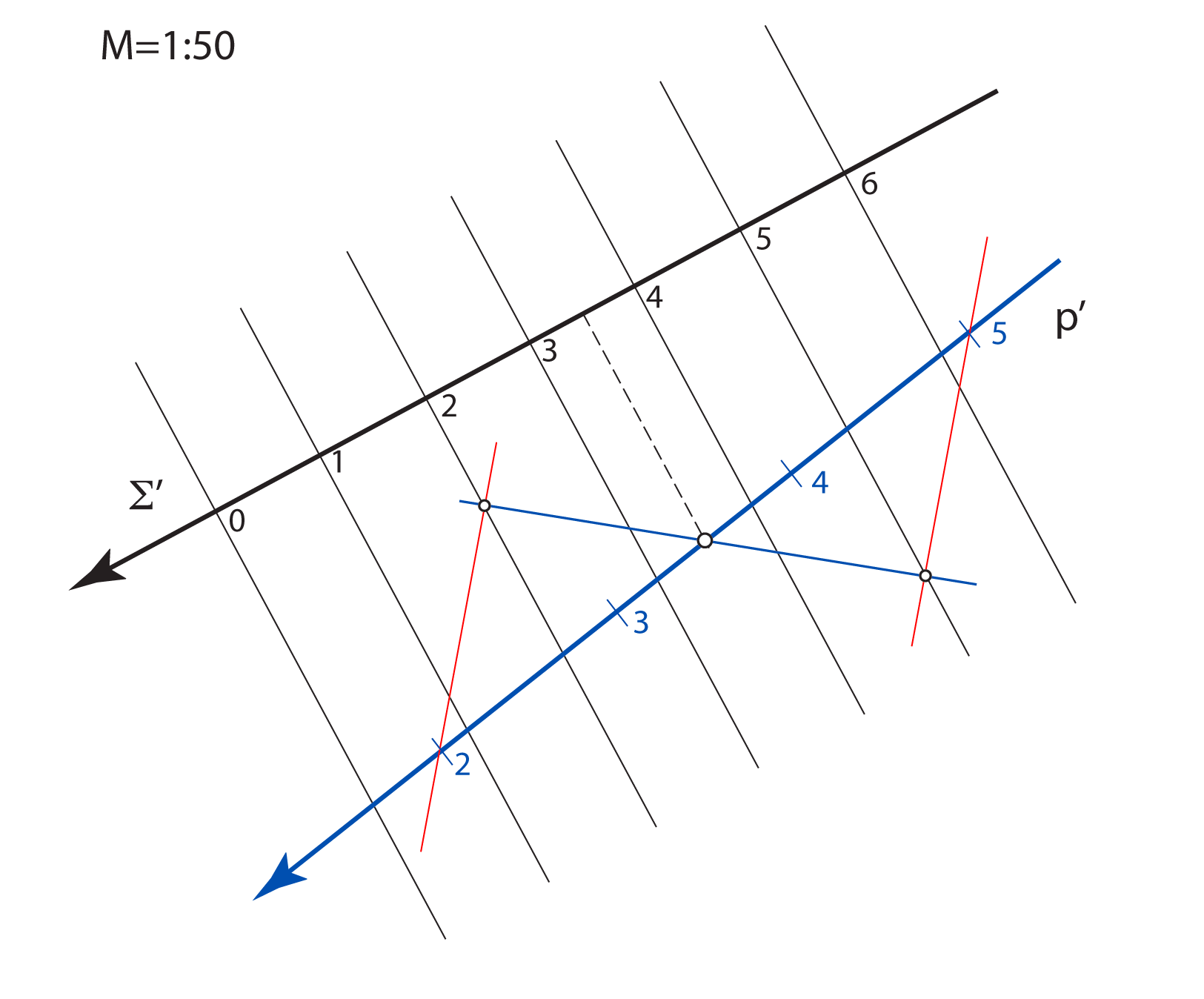
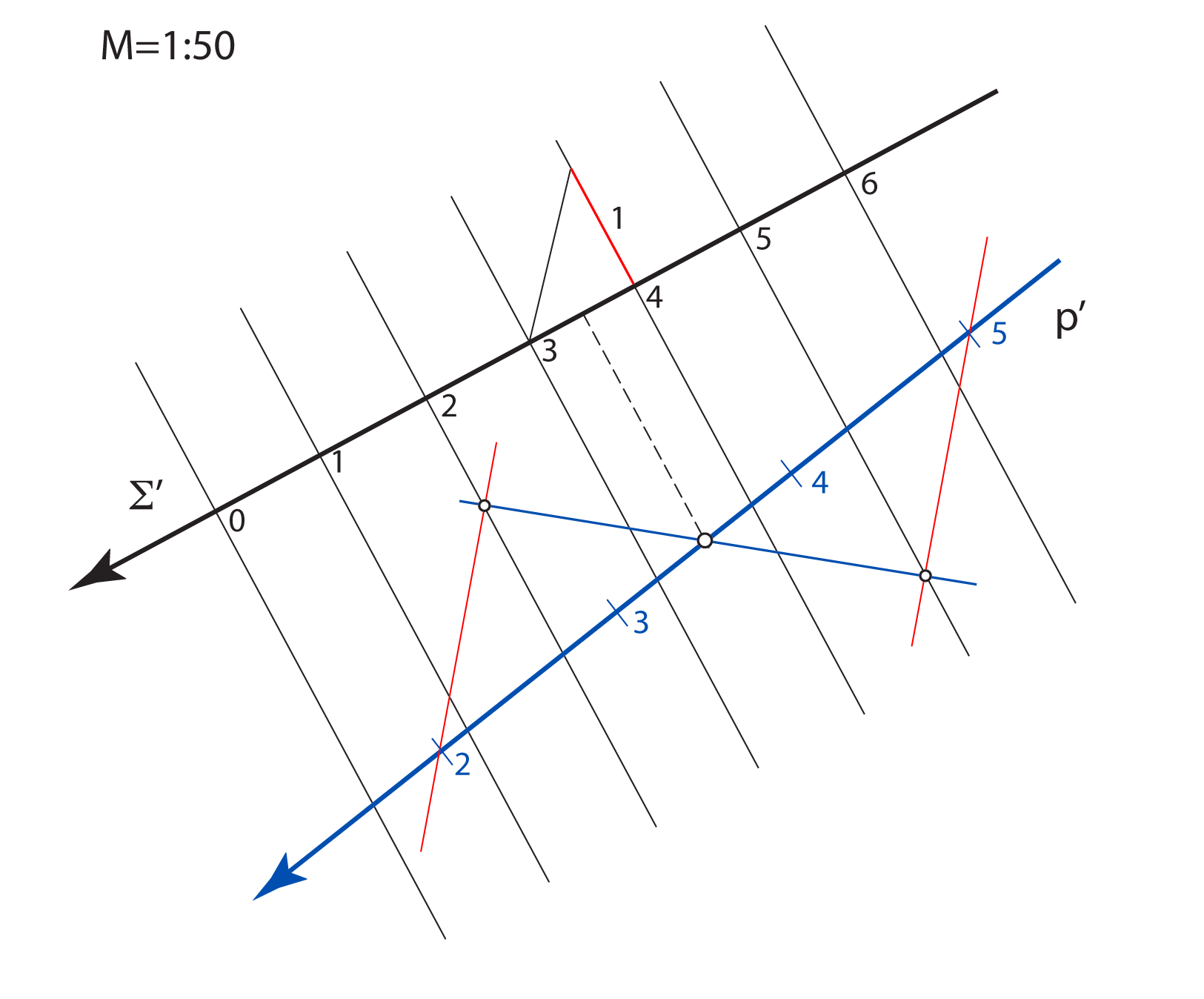
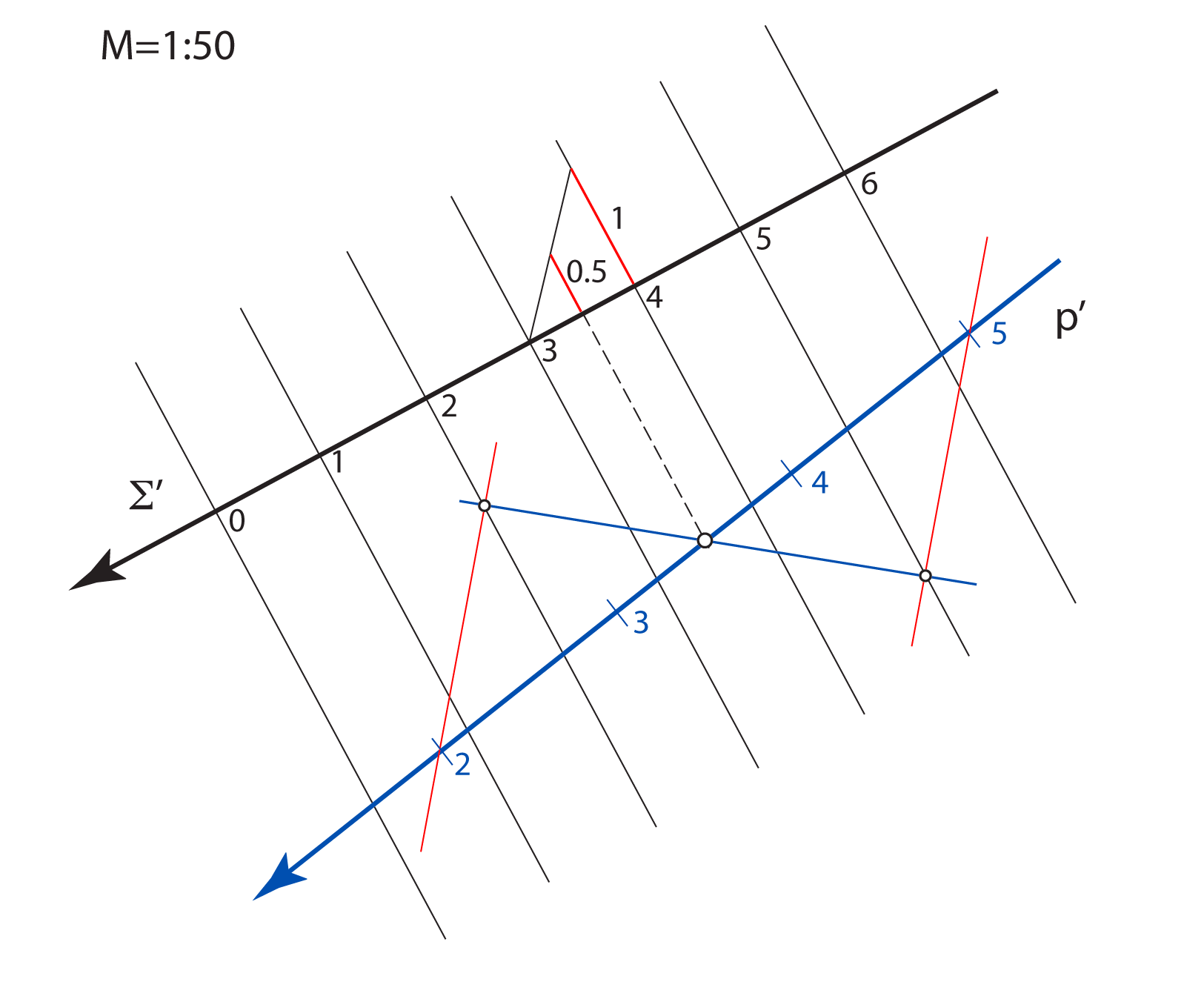
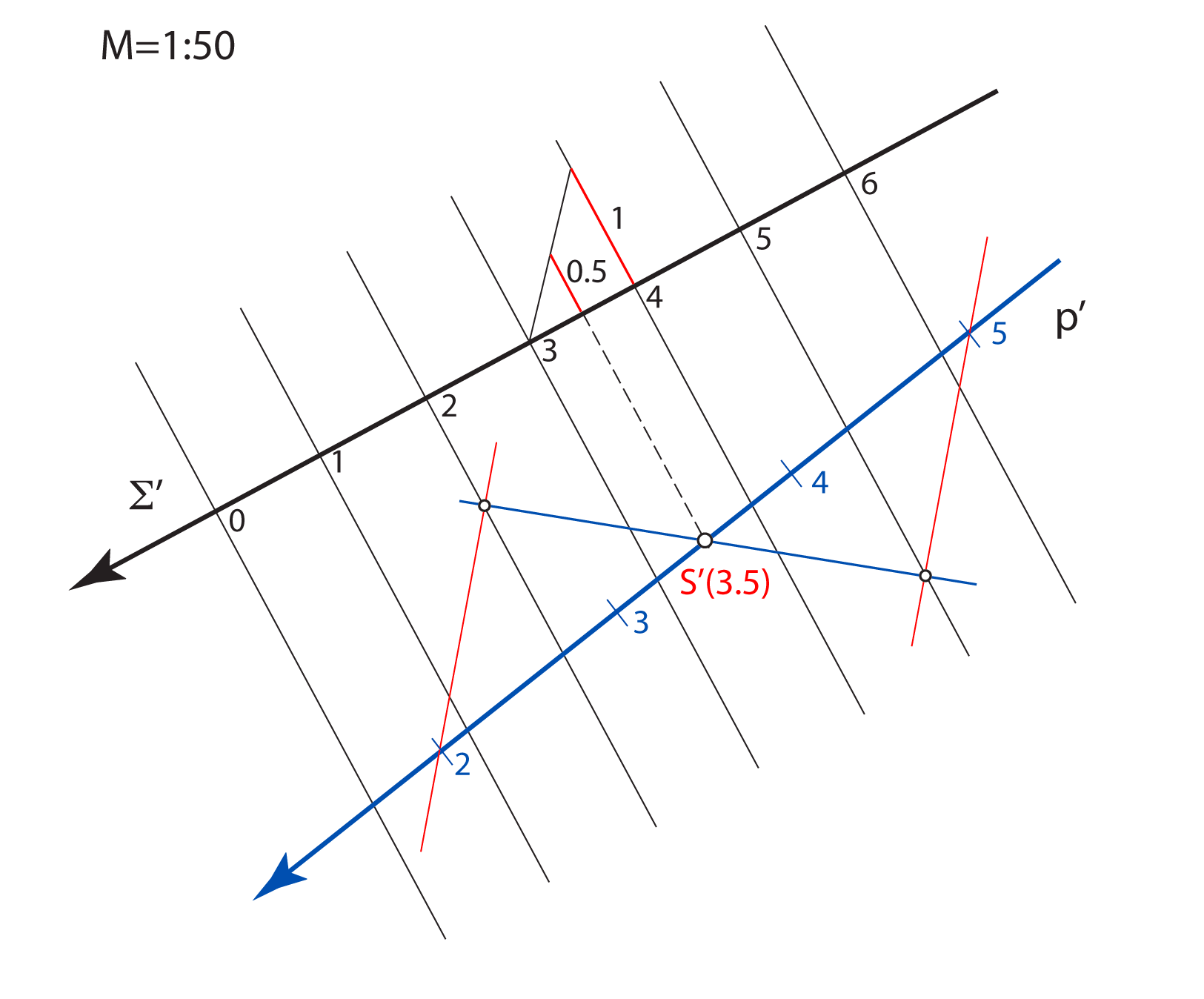
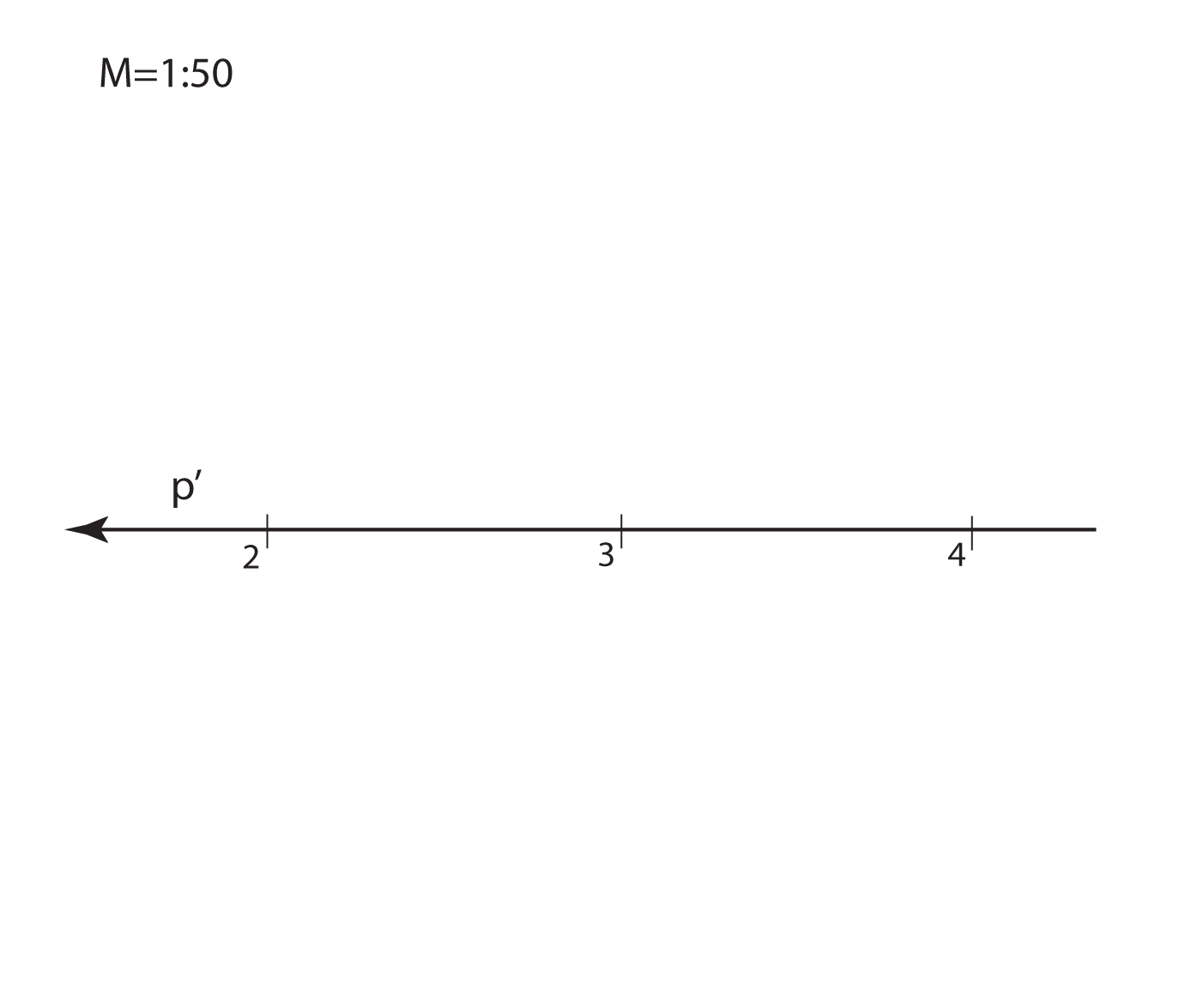
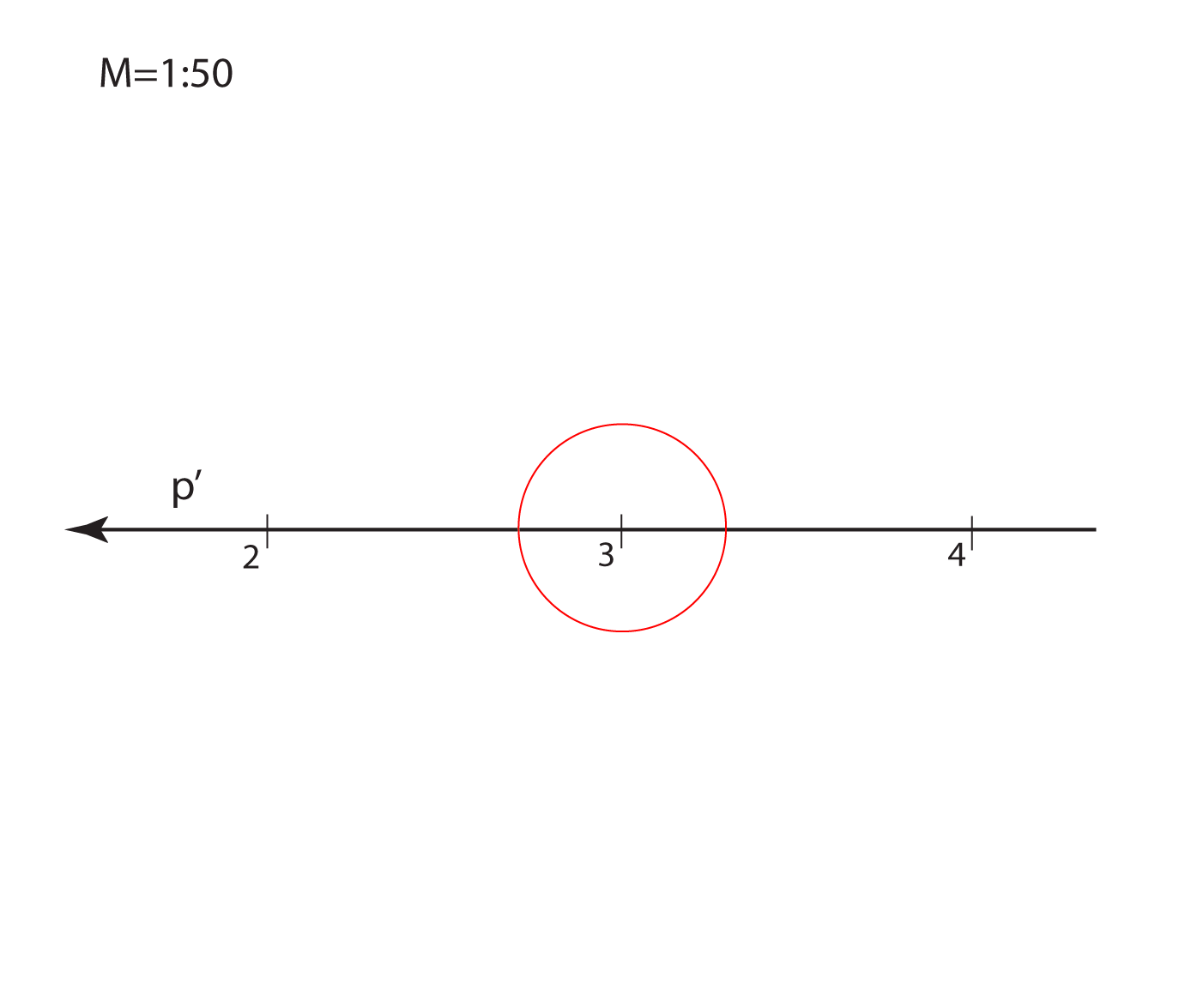
Kote odnosno brojeve koji izražavaju udaljenost točaka od ravnine projekcije treba povezani s nekom mjernom jedinicom.
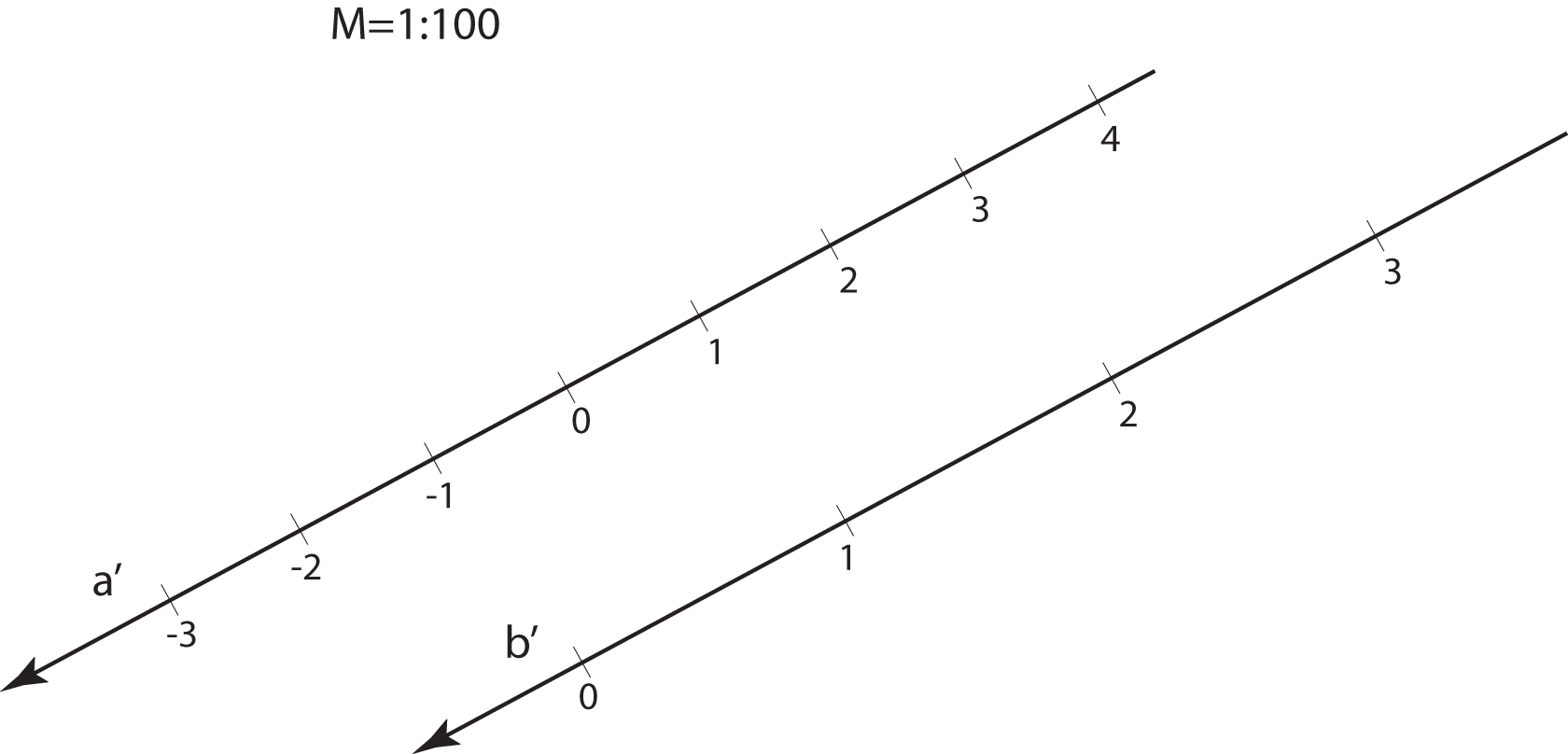
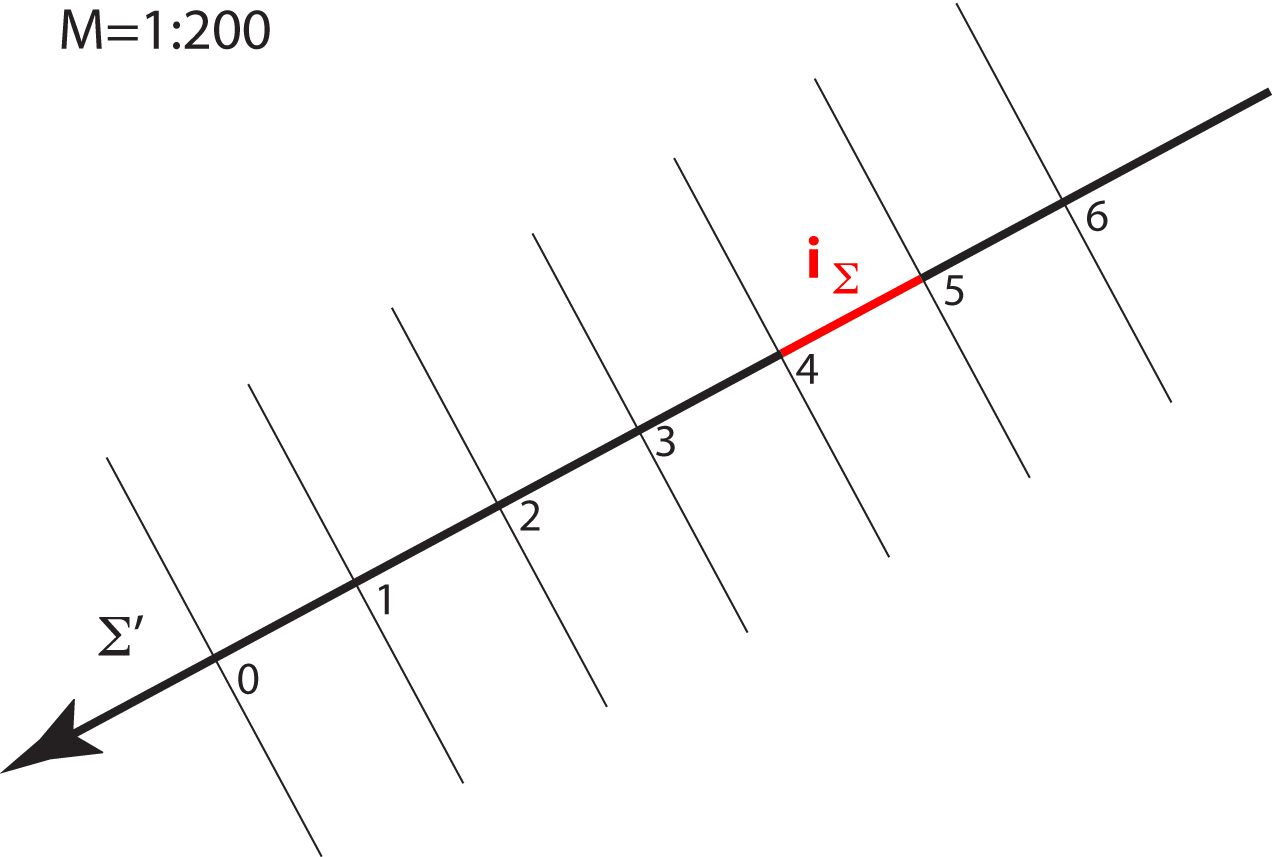
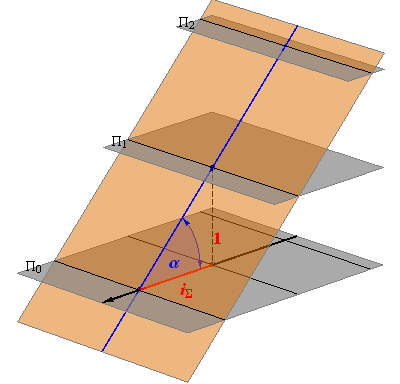
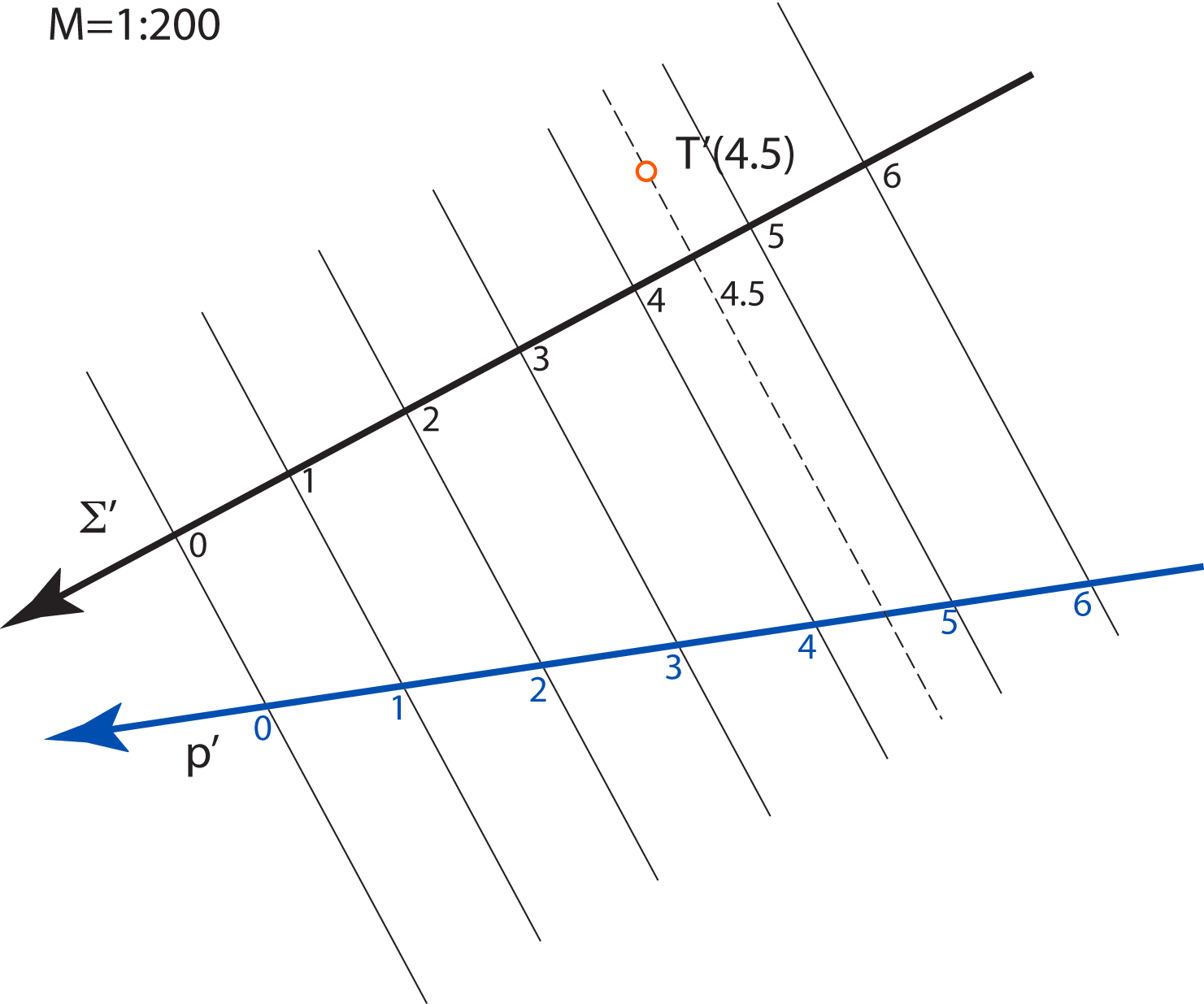
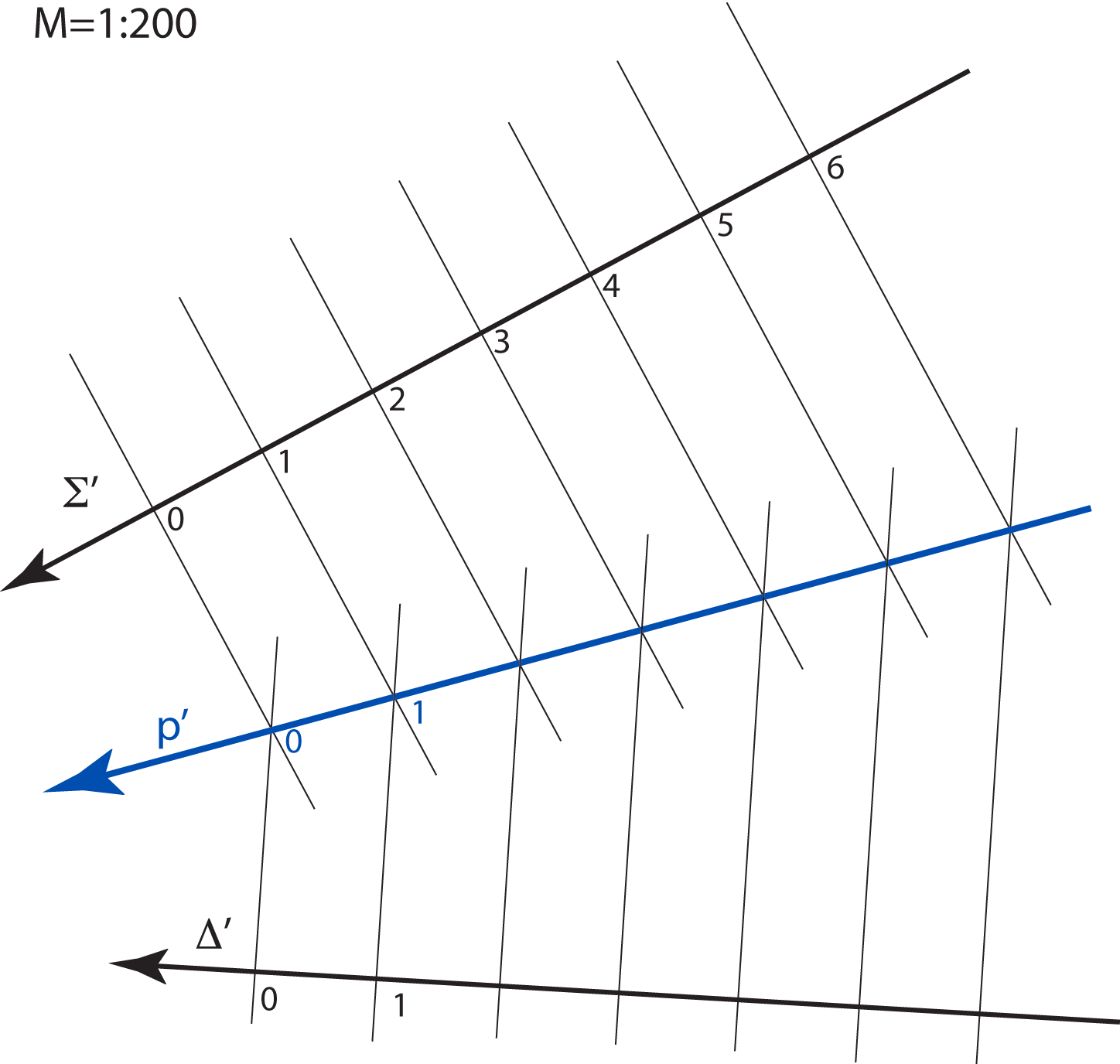
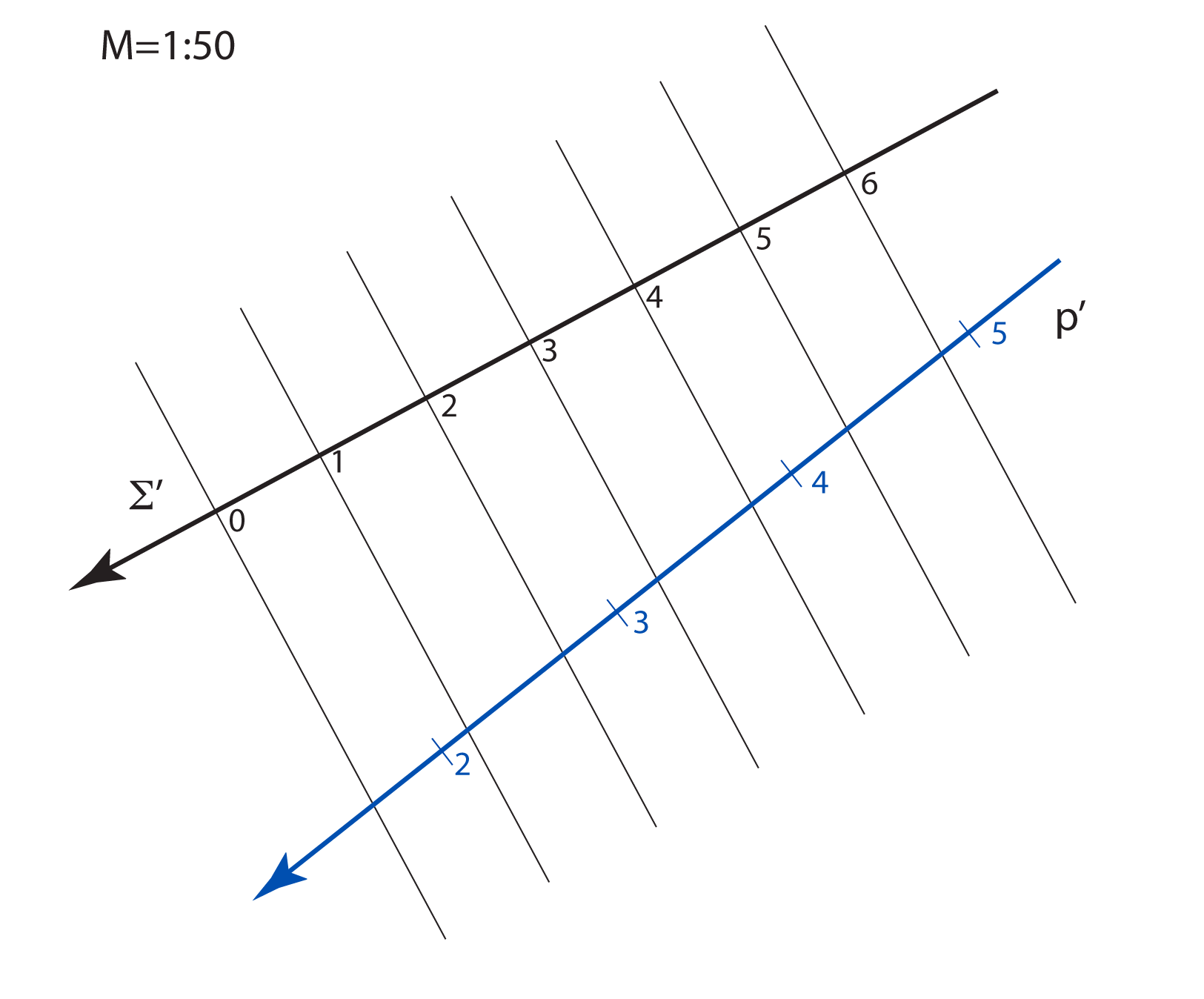
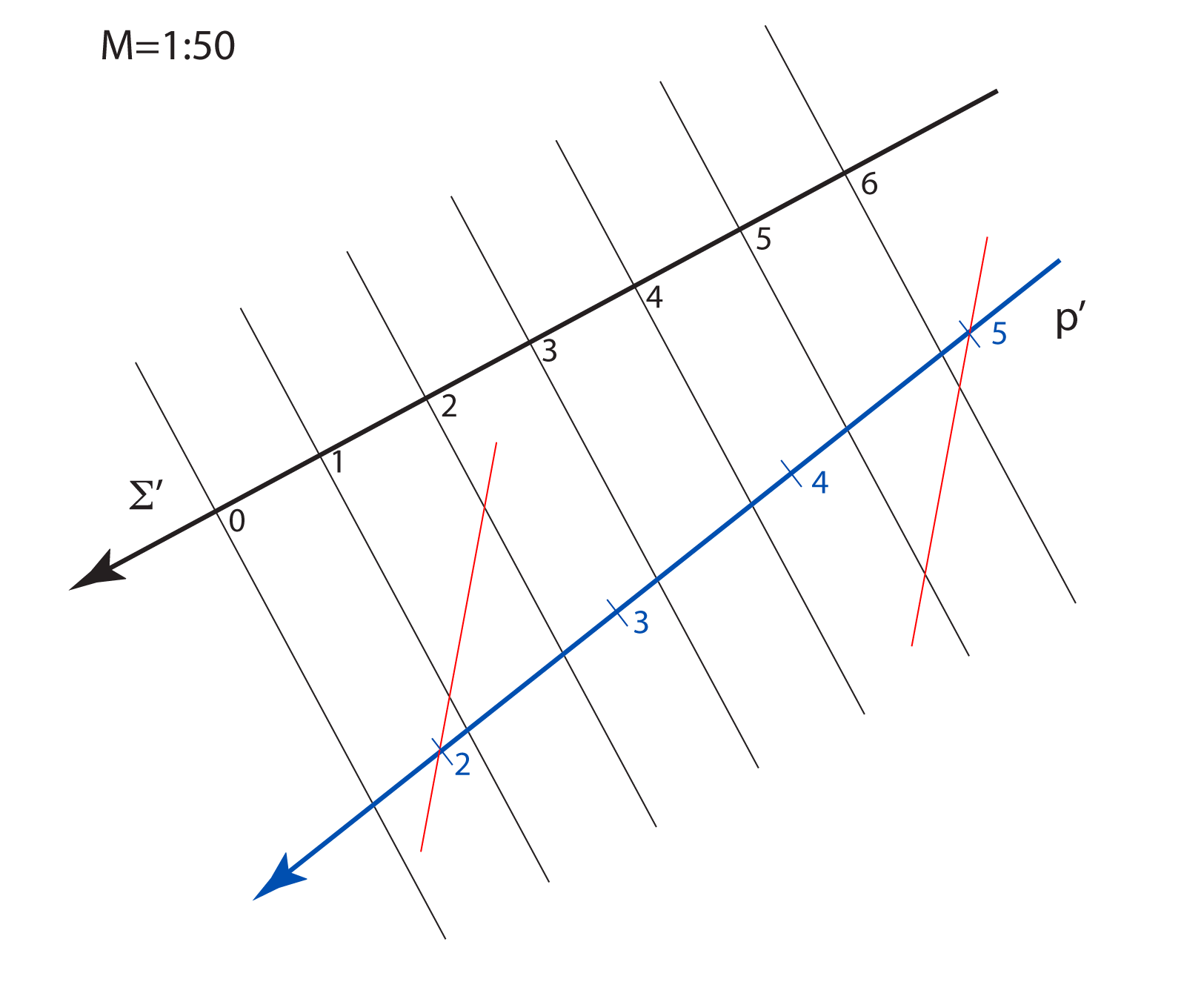
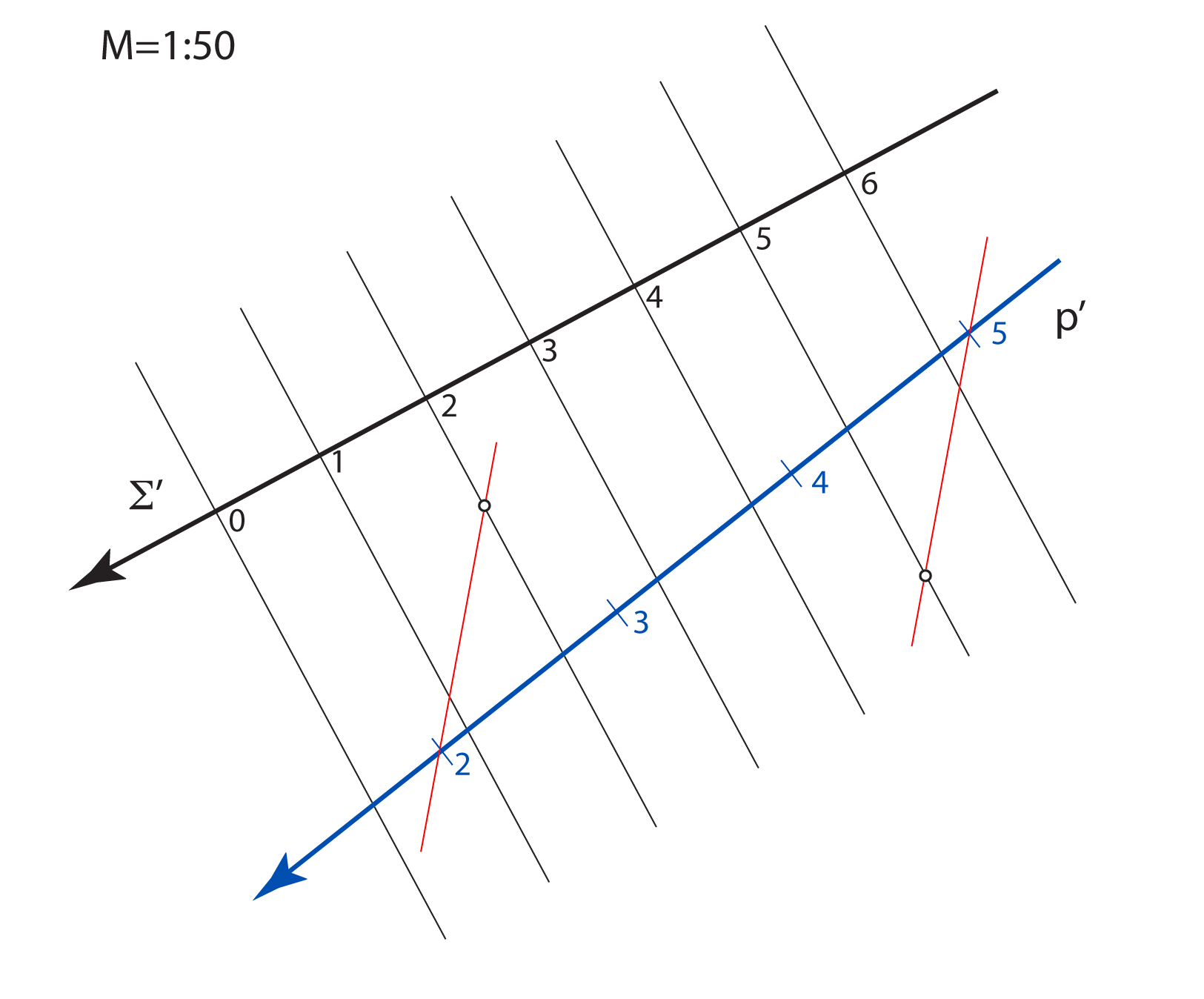
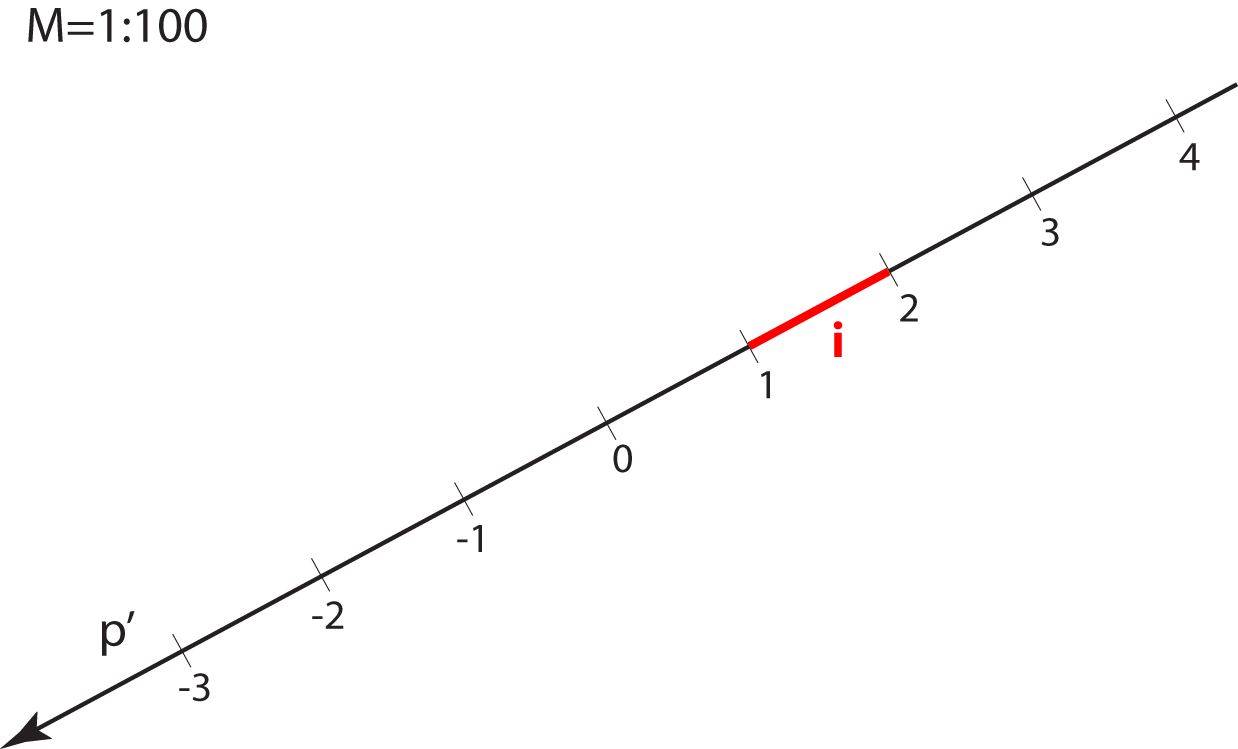
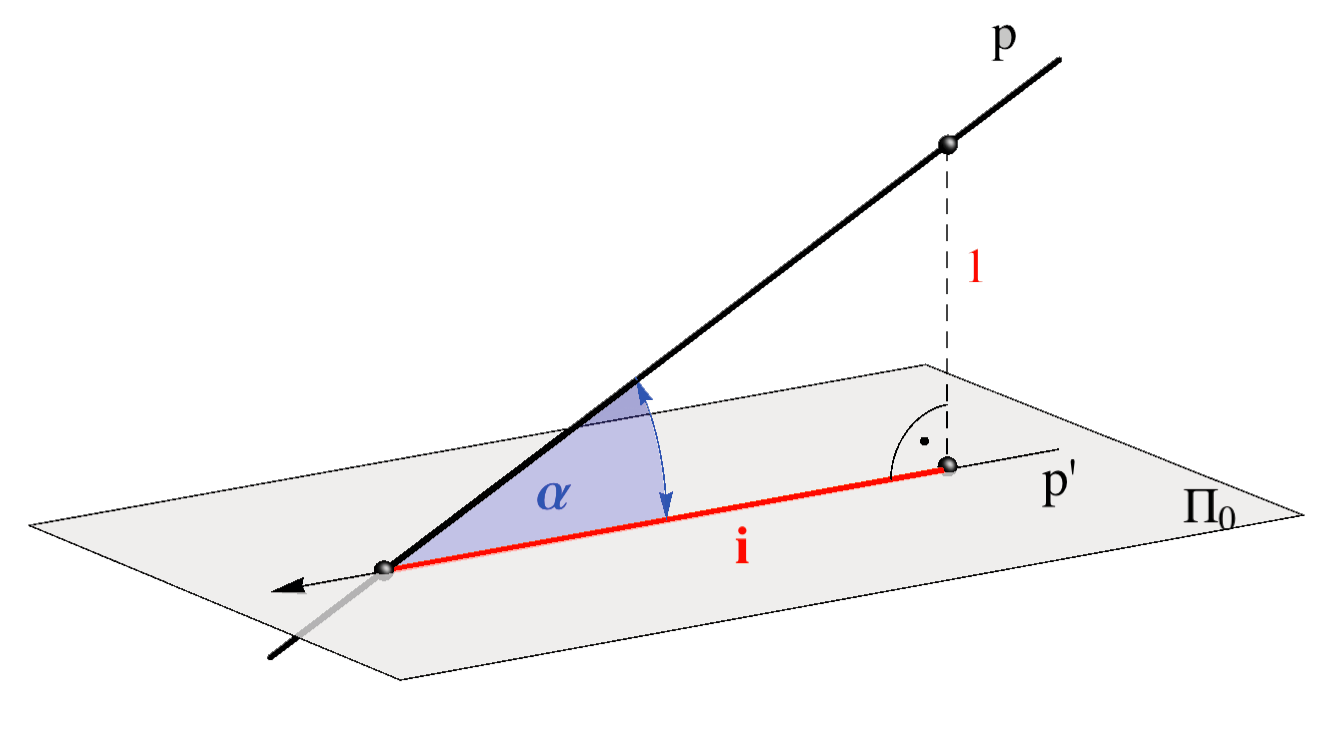
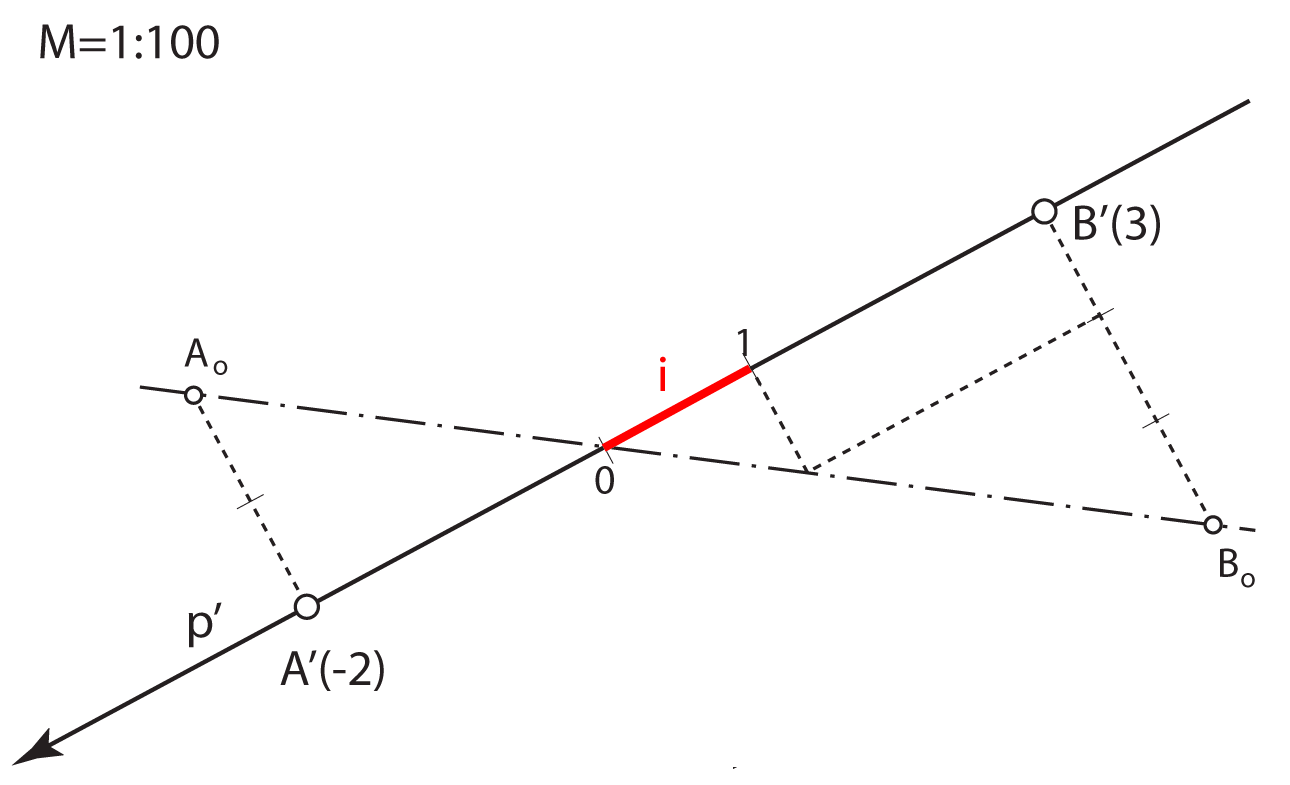
Za osnovnu mjernu jedinicu u kotiranoj projekciji odabiremo 1 metar. Sasvim je razumljivo da na crtežu nije moguće takve jedinice prikazivati u pravoj veličini. Stoga objekte u kotiranoj projekciji crtamo umanjeno, u mjerilu koje nazivamo mjerilom slike. Mjerilo slike zadajemo u obliku kvocijenta \(\small \mathbf {M=1:a}\), što znači da će prava veličina dužine u horizontalnoj ravnini, koja je u ravnini slike dugačka \(1\, m\), na crtežu iznositi \(\mathbf {\frac{1}{a}}\,m\).

Na svakoj slici u kotiranoj projekciji mjerilo mora biti naznačeno.

IZRAČUNAJTE koliko iznosi \("1\, m"\) u mjerilima:
\( M=1:25\), \( M=1:50\), \( M=1:100\), \( M=1:125\), \( M=1:200\), \( M=1:250\), \( M=1:400\), \( M=1:500\).

Kotirana projekcija točke

Točka se u kotiranoj projekciji prikazuje njezinom ortogonalnom projekcijom na ravninu slike i kotom. Pritom kota točke izražava udaljenost točke od ravnine slike u metrima. U našim će primjerima ravnina slike redovito biti tlocrtna ravnina.


Slika 2.153a

Slika 2.153b:

Točka \(\small A\) se nalazi 2 m ispod, a točka \(\small B\) 3 m iznad ravnine slike.


Kotirana projekcija pravca

Pravac, koji je u općem položaju prema ravnini projekcije, u kotiranoj se projekciji prikazuje svojim tlocrtom na kojem su istaknute projekcije onih njegovih točaka koje imaju cjelobrojne kote. Te točke nazivamo glavnim točkama pravca, a tako zadan pravac graduiranim pravcem. Smjer pada kota točaka na pravcu označujemo strelicom.

Razmak između projekcija dviju susjednih točaka cjelobrojnih kota, odnosno projekcija dviju točaka pravca kojima je visinska razlika 1m, nazivamo intervalom\(^*\) pravca. Uočite da su svi intervali nekog pravca jednaki. Nagib pravca je tangens kuta što ga taj pravac zatvara s ravninom projekcije.
\(^*\) Prometnice GFZ: interval pravca \(\rightarrow\) korak za ekvidistancu 1.
  • Interval i nagib pravca su recipročni brojevi (vidi sliku 2.154b).

Slika 2.154a: Graduirani pravac s istaknutim intervalom.





Slika 2.154b: \( n_p = \tan\alpha = \frac{1}{i}\)



Zadatak 1: Graduirajte pravac koji prolazi točkama \(\small A\) i \(\small B\).
Zadatak se rješava pomoću prevaljivanja pravca u ravninu projekcije, a postupak prevaljivanja isti je kao u Mongeovom projiciranju, osim što su udaljenosti točaka od ravnine projekcije određene kotama, a ne nacrtima.




Slika 2.155

Međusobni položaji dvaju pravaca


Slika 2.156a:


Pravci koji se sijeku - sjecište projekcija ima istu kotu na oba pravca.

Slika 2.156b:


Paralelni pravci - paralelne projekcije, isti smjer pada kota i jednaki intervali.


Slika 2.156c:


Mimosmjerni pravci - projekcije se sijeku, ali to sjecište ima različite kote na zadanim pravcima.

Slika 2.156d:
Mimosmjerni pravci - paralelne projekcije, a različiti intervali.

Pravci u posebnom položaju prema ravnini projekcije

  • Ako je pravac okomit na ravninu projekcije, tada je on zraka projiciranja i projekcija mu je točka, a njegov je interval 0.
  • Ako je pravac paralelan s ravninom projekcije, sve njegove točke imaju iste kote pa interval nije definiran.
Općenito, linije koje sadrže točke istih kota imaju posebnu ulogu u kotiranoj projekciji. Ako leže na nekoj plohi, nazivamo ih slojnicama plohe. Ako je ploha ravnina, onda su njezine slojnice pravci paralelni s ravninom projekcije. Te smo pravce kod Mongeovog projiciranja nazivali sutražnicama 1. skupine.

Kotirana projekcija ravnine

Ravnina se u kotiranoj projekciji prikazuje glavnim slojnicama i mjerilom nagiba. Glavne slojnice ravnine su one slojnice kojima su kote točaka cijeli brojevi, odnosno one su presječnice ravnine s glavnim nivo-ravninama. Mjerilo nagiba je bilo koji pravac ravnine koji je okomit na njezine slojnice (bilo koja njezina priklonica 1. skupine).

Nagib i interval ravnine jednaki su nagibu i intervalu njezinog mjerila nagiba.

Slika 2.157a: Ravnina u kotiranoj projekciji s istaknutim intervalom ravnine.

Slika 2.157b

Slika 2.158: Točka \(\small T\) i pravac \(\small p\) leže u ravnini \(\small\Sigma\).



  • Projekcija presječnice dviju ravnina je spojnica sjecišta istoimenih slojnica.

    Slika 2.159: \(\small \Sigma \cap \Delta = p\)



    Zadatak 2: Konstruirajte projekciju probodišta pravca \(\small p\) i ravnine \(\small\Sigma\).
    Postupak konstrukcije probodišta pravca i ravnine je isti kao kod Mongeova projiciranja, samo što kao pomoćnu ravninu ne odabiremo projicirajuću ravninu.

    Slika 2.160



    Zadatak 3: Konstruirajte nekoliko slojnica i mjerila nagiba ravnina koje sadrže zadani pravac \(\small p\), a nagib im je \(\small n=2\).
    Ovaj će zadatak biti vrlo važan u rješavanju problema na terenu - posebno za postavljanje ravnina nasipa i usjeka na prometnicama u nagibu.

    Slika 2.161a

    Slika 2.161b






    Sonja Gorjanc, Helena Koncul - 3DGeomTeh - Razvojni projekt Sveučilišta u Zagrebu