Deskriptivna (nacrtna ili opisna) geometrija bavi se egzaktnim metodama koje omogućuju:
- prikaz objekata trodimenzionalnog prostora u nekoj dvodimenzionalnoj ravnini
- rješavanje prostornih problema primjenom konstruktivnih postupaka u ravnini
- rekonstrukciju prostornih objekata na temelju njihovih ravninskih prikaza.
Metode nacrtne geometrije temelje se na projiciranju, odnosno preslikavanju trodimenzionalnoga euklidskog prostora na dvodimenzionalnu euklidsku ravninu. Pravce i ravnine (osnovne elemente prostora), kao i sve ostale prostorne objekte, promatramo kao skupove točaka. Stoga je za određivanje projiciranja dovoljno definirati način projiciranja točke. Razlikujemo dvije osnovne vrste projiciranja, centralno i paralelno.
Centralno projiciranje
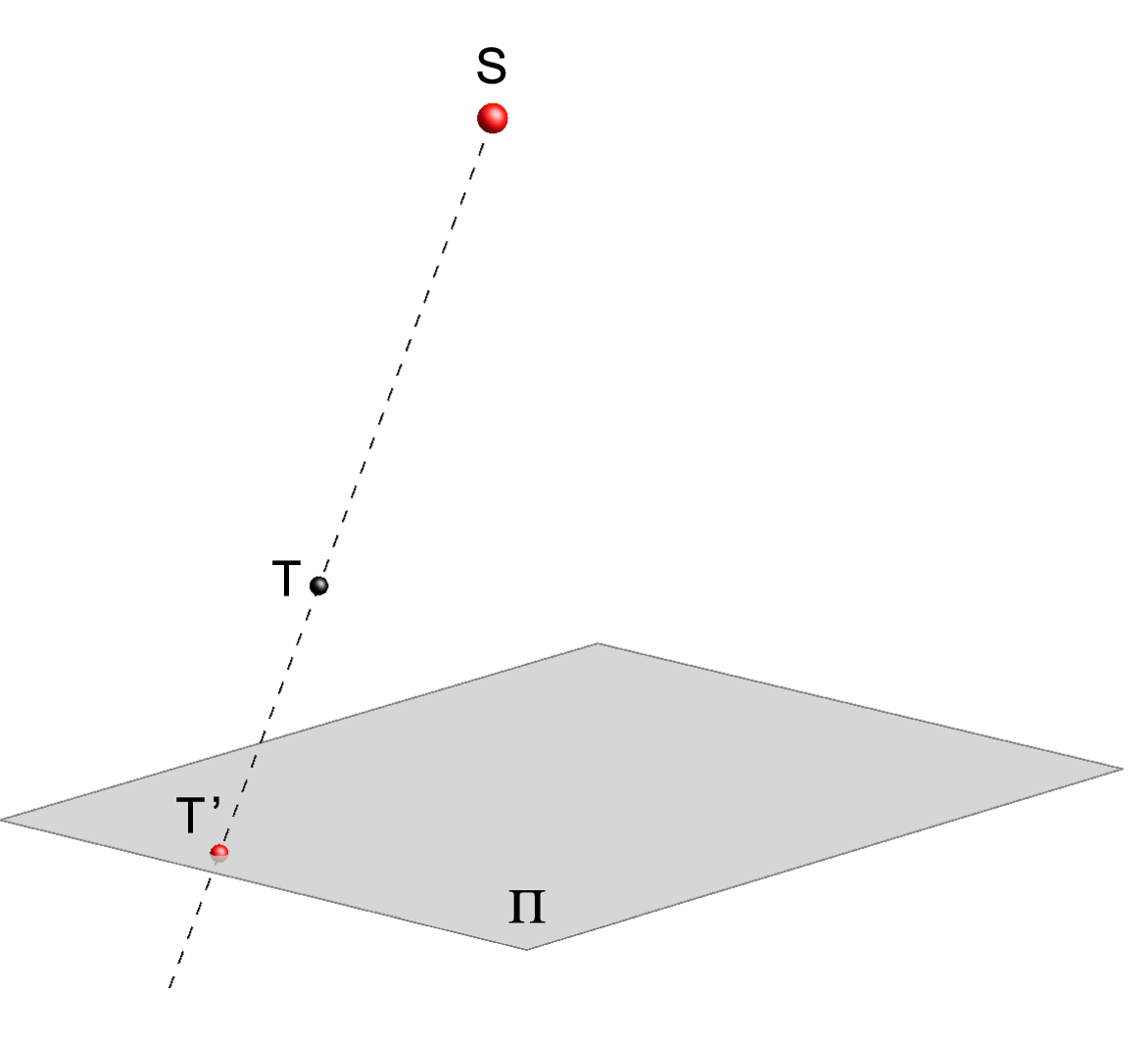
Neka su u prostoru dane ravnina \(\small \Pi\) i točka \({\small S}\) u konačnosti koja ne leži u ravnini \({\small\Pi}\) (\({\small S\notin \Pi}\)).
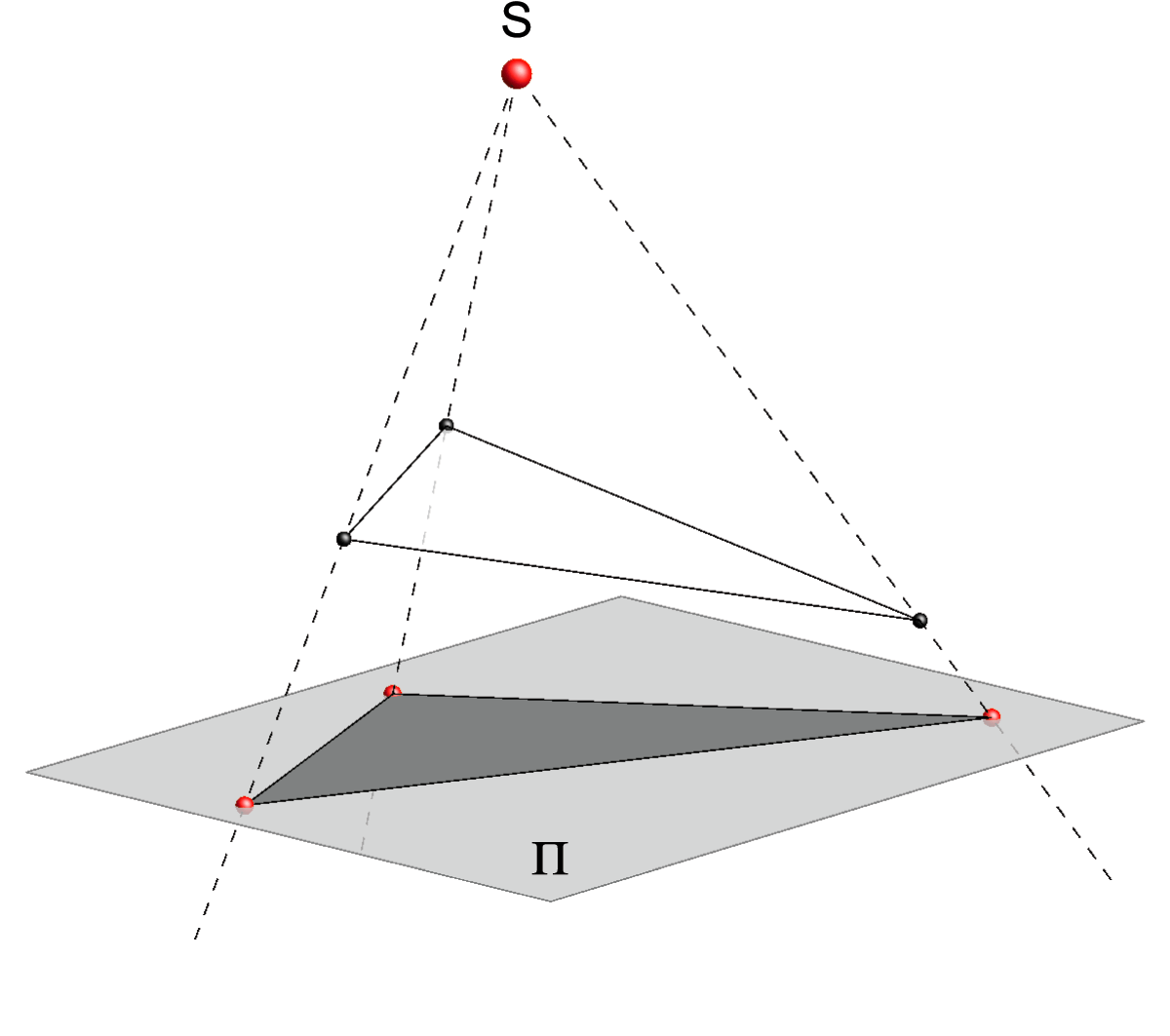
Preslikavanje koje svakoj točki \({\small T\neq S}\) pridružuje točku \({\small T'}\) (probodište pravca \({\small ST}\) i ravnine \({\small \Pi}\)) nazivamo centralnom projekcijom na ravninu \({\small \Pi}\).
Točku \({\small S}\) nazivamo središtem (centrom), a pravce \({\small ST}\) zrakama te centralne projekcije. Ravninu \(\small \Pi\) nazivamo ravninom projekcije.
Paralelno projiciranje
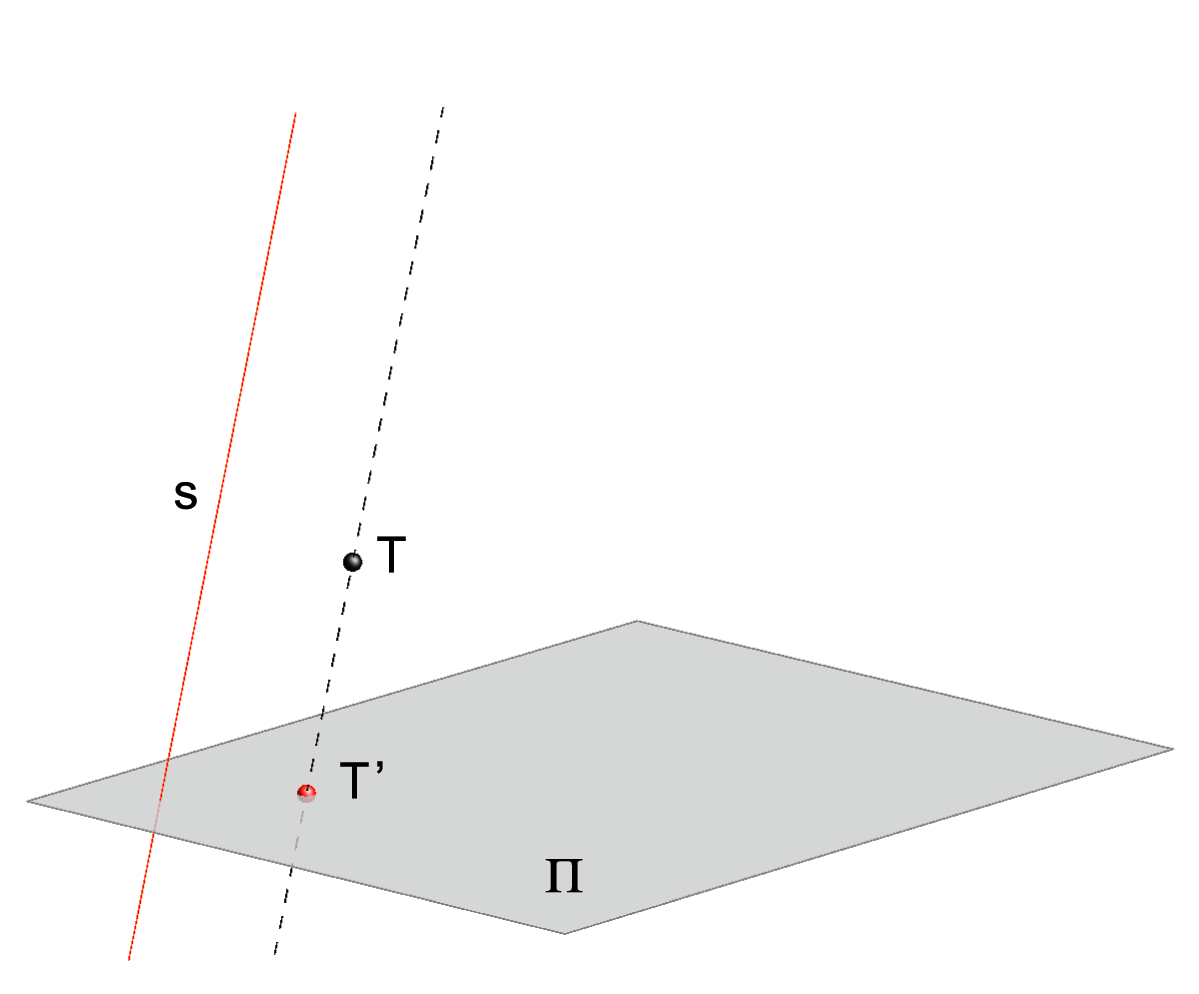
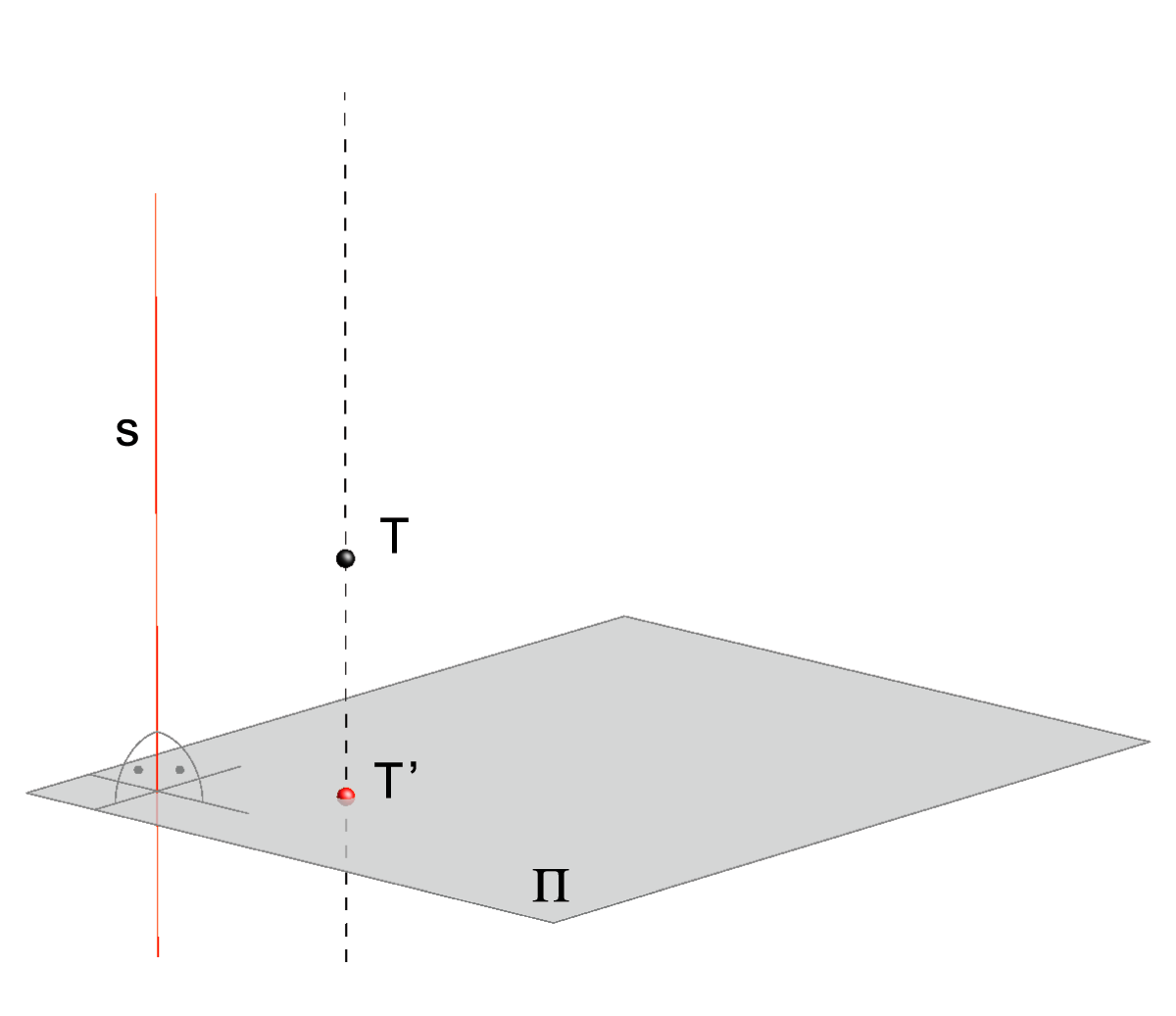
Neka su u prostoru dani ravnina \(\small \Pi\) i pravac \({\small s}\) koji s njom nije paralelan.1
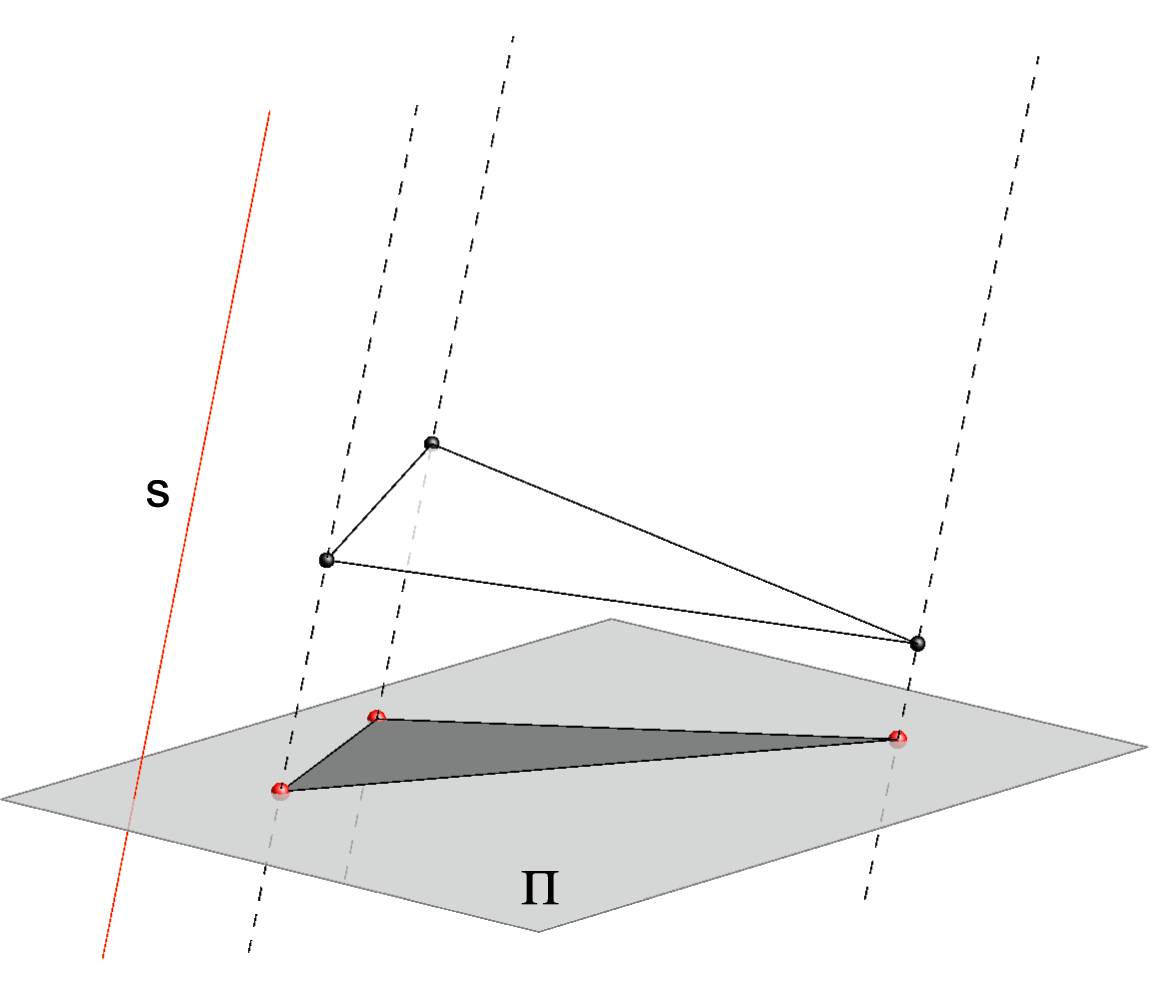
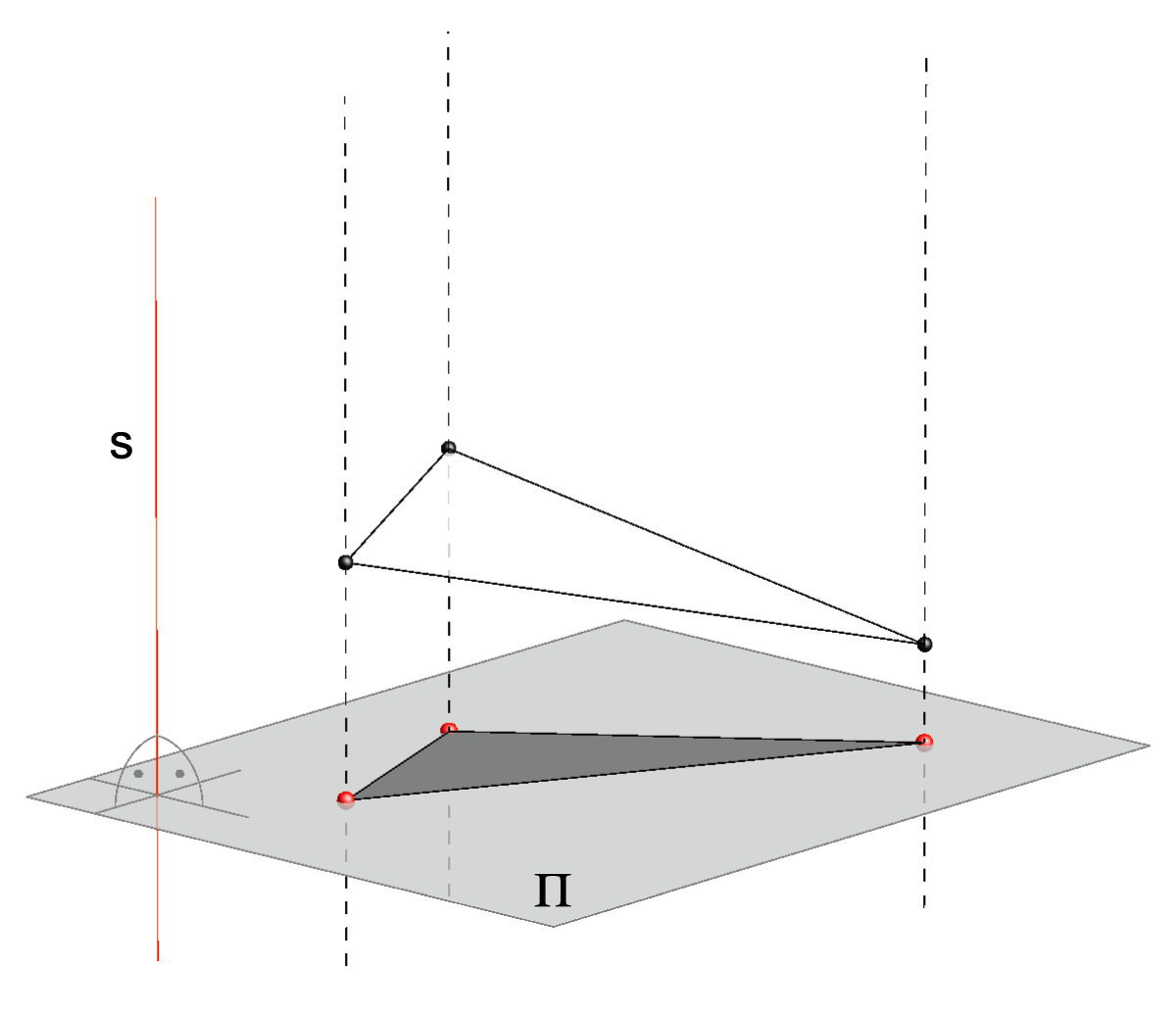
Preslikavanje koje svakoj točki \(\small T\) pridružuje točku \(\small T'\) koja je probodište ravnine \(\small \Pi\) i pravca koji sadrži \(\small T\), a paralelan je sa \(\small s\), nazivamo paralelnom projekcijom na ravninu \(\small\Pi\) u smjeru \(\small s\).2
Pravce paralelne s pravcem \(\small s\) nazivamo zrakama projiciranja, a \(\small\Pi\) ravninom projekcije.
Ako su zrake projiciranja okomite na ravninu projekcije, onda paralelnu projekciju nazivamo ortogonalnom projekcijom.
Za sve ostale slučajeve koristimo naziv kosa paralelna projekcija.
1 Za pravac koji leži u ravnini također smatramo da je s njom paralelan.
2 U proširenom euklidskom prostoru paralelnu projekciju možemo interpretirati kao centralnu sa središtem u beskonačnosti. Naime, tada iz činjenice \(\small S^\infty\notin\Pi\) slijedi da je \(\small S^\infty\) beskonačno daleka točka nekog pravca koji nije paralelan s ravninom \(\small\Pi\).