Tangencijalna ravnina i normala u regularnoj točki plohe

Svakom točkom plohe prolazi beskonačno mnogo krivulja plohe. Za neku točku \(\small T\in\Phi\) promatramo tangente plohe \(\small \Phi\) kojima je točka \(\small T\) diralište.

  • Za točku plohe kažemo da je regularna ako sve tangente plohe kojima je \(\small T\) diralište leže u jednoj ravnini
  • Tangencijalna ili dirna ravnina plohe u nekoj njezinoj regularnoj točki \(\small T\) ravnina je koja sadrži sve tangente plohe s diralištem u \(\small T\), odnosno tangente s diralištem u \(\small T\) svih onih krivulja plohe koje prolaze točkom \(\small T\)
  • Normala plohe u nekoj njezinoj regularnoj točki \(\small T\) je pravac koji prolazi točkom \(\small T\) i okomit je na tangencijalnu ravninu plohe u točki \(\small T\)

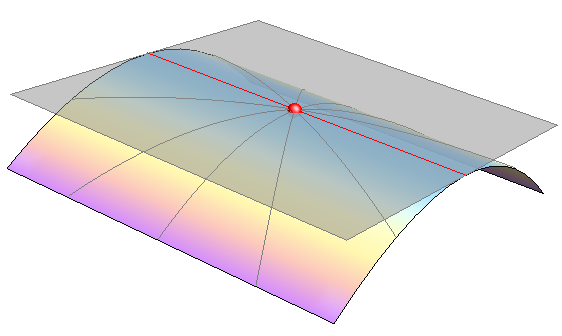
Na slici 308 prikazana je ploha \(\small \Phi\) te njezina tangencijalna ravnina \(\small \Delta\) i normala \(\small n\) u regularnoj točki \(\small T\).

Slika 308

U svakoj regularnoj točki plohe postoje jedinstvena dirna ravnina i normala plohe. Dirna ravnina u nekoj točki plohe određena je s bilo koje dvije tangente plohe u toj točki (vidi animaciju 15).

Animacija 15

Singularne točke plohe

\(\small S\) je singularna točka plohe ako tangente plohe, s diralištem u \(\small S\), ne leže u jednoj ravnini. To su npr. točke u kojma ploha samu sebe siječe ili dodiruje.

U takvim točkama tangente plohe tvore neki stožac ili dvije ili više ravnina.

Ako su sve točke neke linije na plohi singularne, onda tu liniju nazivamo singularnom linijom plohe.

Slika 309: Singularna točka plohe
Slika 310: Singularni pravac plohe

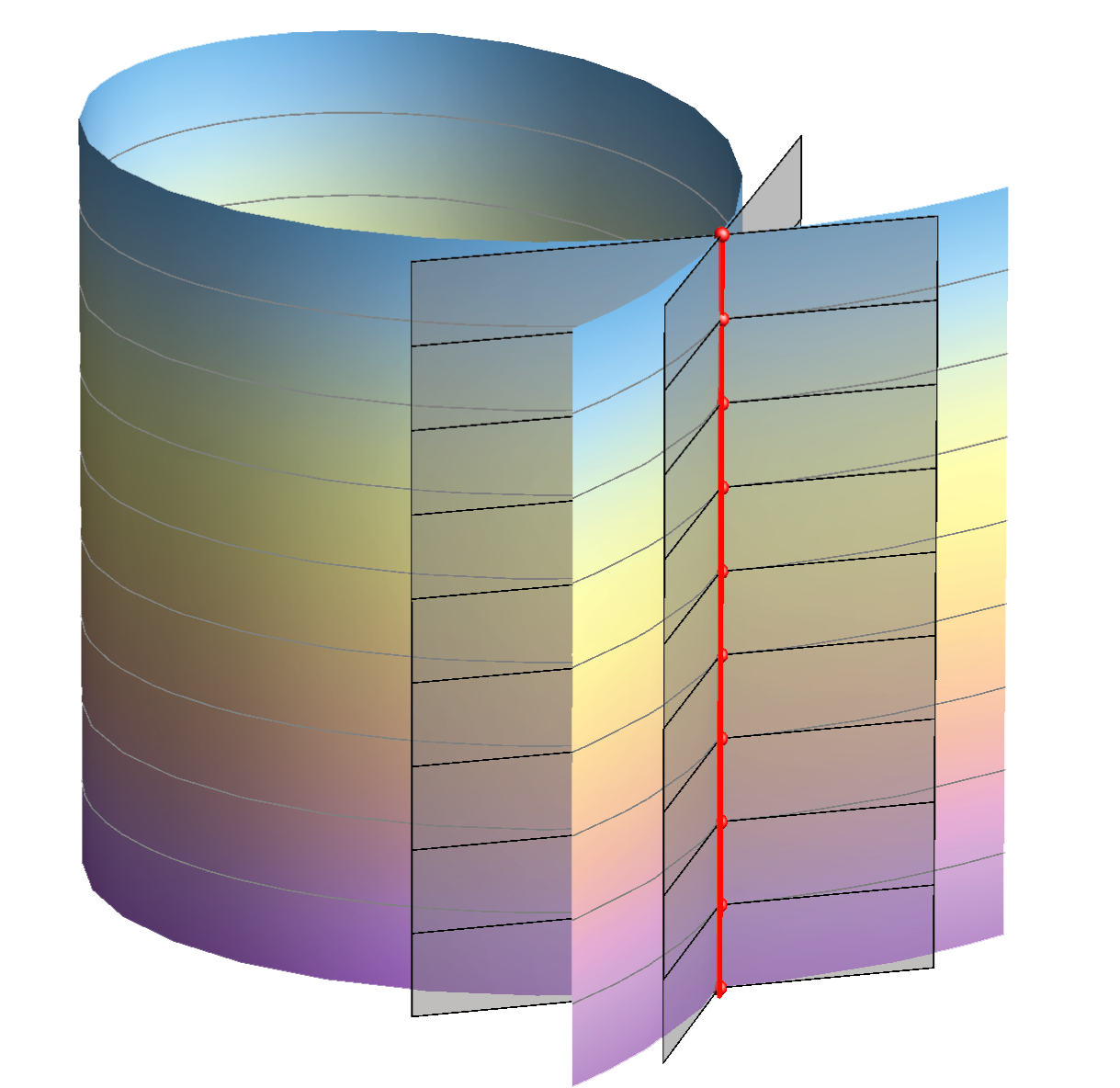
Pravčaste plohe

Plohu nazivamo pravčastom ako kroz svaku njezinu točku prolazi barem jedan pravac koji cijeli leži na toj plohi.

Te pravce nazivamo izvodnicama pravčaste plohe.

  • Tangencijalna ravnina u nekoj točki pravčaste plohe uvijek sadrži izvodnicu koja prolazi tom točkom
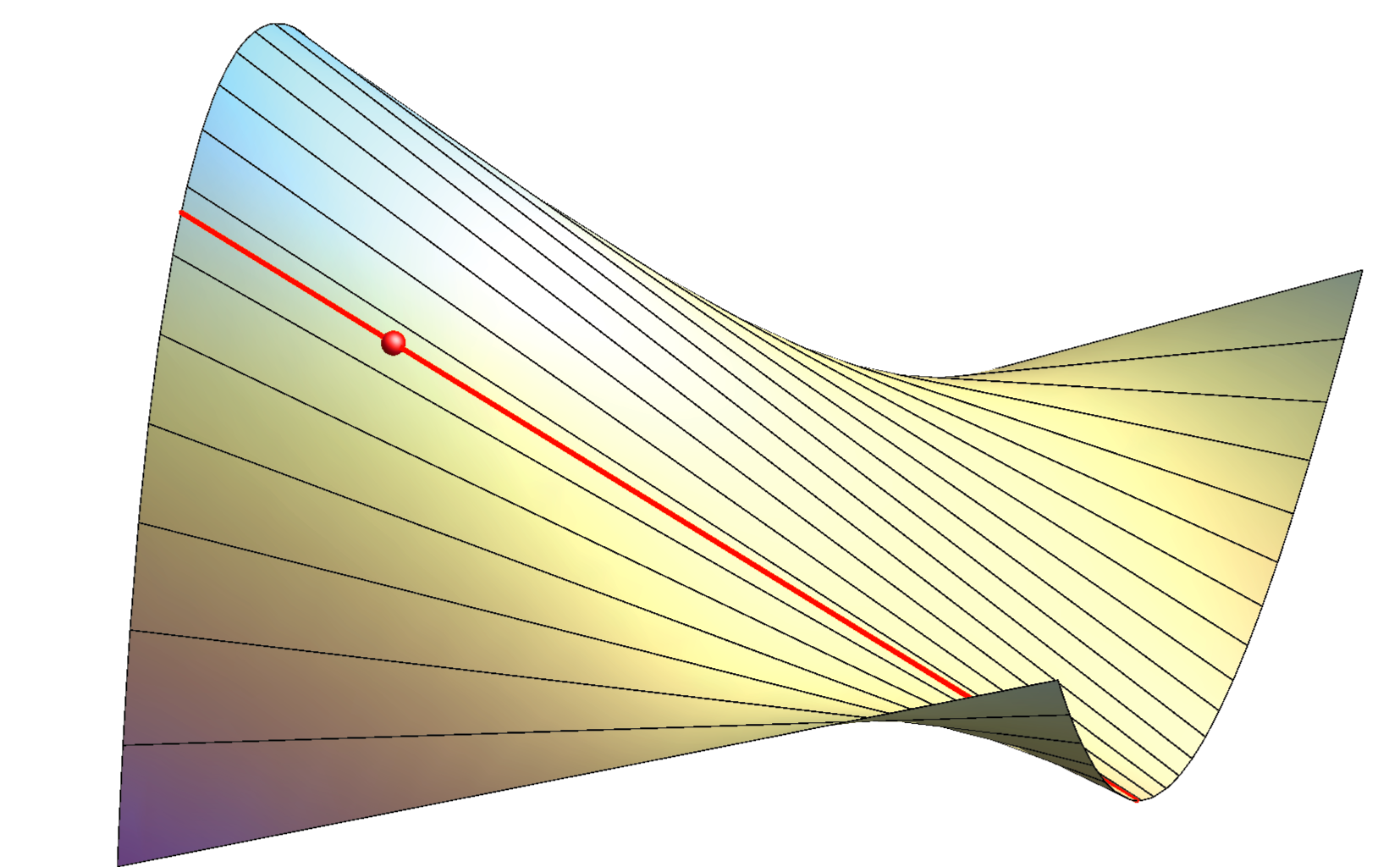
Slika 311: Izvodnica kroz odabranu točku pravčaste plohe
Animacija 16: Dirna ravnina duž jedne izvodnice pravčaste plohe

Vrste regularnih točaka plohe

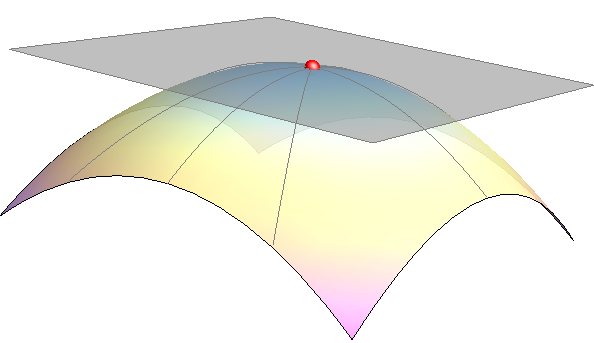
  • Točku plohe nazivamo eliptičkom ako se ploha u njezinoj okolini nalazi s iste strane tangencijalne ravnine
  • Točku plohe nazivamo hiperboličkom ako se ploha u njezinoj okolini nalazi s različitih strana tangencijalne ravnine. Smjerove u tangencijalnoj ravnini koji razdvajaju okolinu plohe nazivamo asimptotskim smjerovima plohe u toj točki
  • Za točku plohe kažemo da je parabolička ako se ploha u njezinoj okolini nalazi s iste strane tangencijalne ravnine, ali je ta ravnina tangencijalna i za sve točke neke krivulje na plohi koje leže u promatranoj okolini točke
Slika 312: Eliptička točka plohe
Slika 313: Hiperbolička točka plohe
Slika 314: Parabolička točka plohe
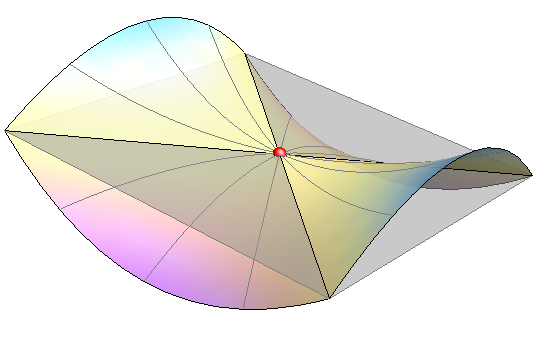
  • Plohe kojima su sve točke paraboličke nazivamo jednostruko zakrivljenim plohama. Sve takve plohe su pravčaste i duž svake izvodnice imaju jedinstvenu tangencijalnu ravninu. Njihovo je svojstvo da se bez istezanja i kidanja mogu razviti u ravninu pa ih nazivamo razvojnim plohama. Stošci i valjci su primjeri takvih ploha
  • Dijelove plohe (ili cijele plohe) koji sadrže samo eliptičke ili samo hiperboličke točke nazivamo dvostruko zakrivljenim dijelovima (ili plohama)
    • Za dijelove koji sadrže samo eliptičke točke kažemo da su dvostruko istosmjerno zakrivljeni
    • Za dijelove koji sadrže samo hiperboličke točke kažemo da su dvostruko protusmjerno zakrivljeni
  • Dvostruko zakrivljene plohe ne mogu se bez kidanja i istezanja razviti u ravninu, nazivamo ih vitoperim plohama