Prodorna krivulja dviju ploha koje su stošci i valjci 2. stupnja te sfere jest prostorna algebarska krivulja 4. reda\(^*\).
\(^*\) Postoje dvije vrste algebarskih prostornih krivulja 4. reda (I. i II. vrste). Krivulje I. vrste prodorne su krivulje dviju kvadrika, a II. vrste dio su raspadnute prostorne krivulje 6. reda koja je presjek jedne pravčaste plohe 3. stupnja i jedne pravčaste plohe 2. stupnja, ako te plohe imaju jedan zajednički pravac i ako je to dvostruki pravac plohe 3. stupnja.
Ovdje ćemo obrađivati samo prostorne krivulje 4. reda I. vrste i to prodorne krivulje stožaca, valjaka i sfera. Takve krivulje mogu imati najviše jednu dvostruku točku, a da ne dođe do njihova raspada.
Razlikujemo tri osnovna oblika pravih prostornih krivulja 4. reda I. vrste:
- jednodijelne
- dvodijelne
- prostorne krivulje 4. reda s jednom dvostrukom točkom
Razlikujemo četiri oblika raspada prostornih krivulja 4. reda:
- krivulja 3. reda i pravac
- dvije krivulje 2. reda
- krivulja 2. reda i dva pravca
- četiri pravca
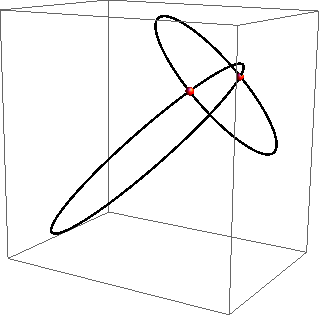
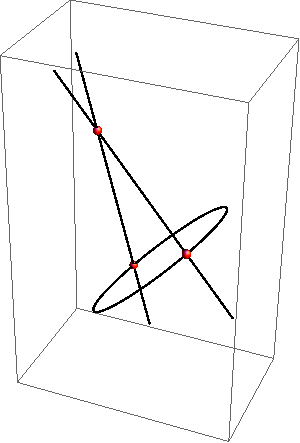
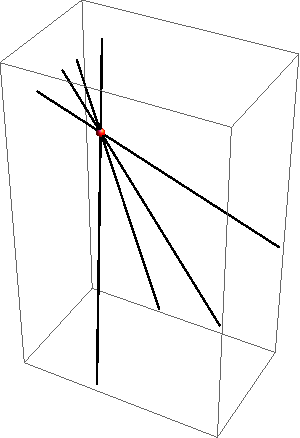
Na slikama 370 - 372 prikazani su primjeri pravih prostornih krivulja 4. reda.
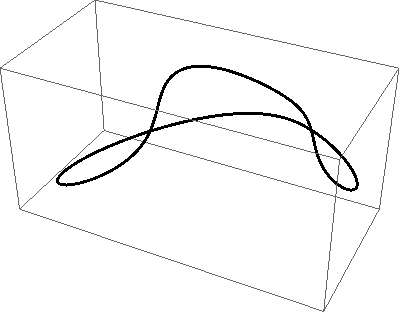
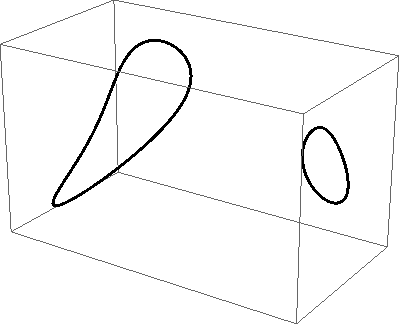
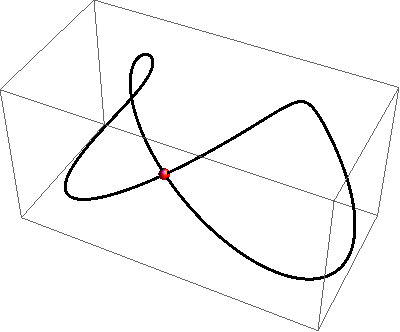
Na slikama 373 - 376 prikazani su primjeri raspadnutih (degeneriranih) prostornih krivulja 4. reda.
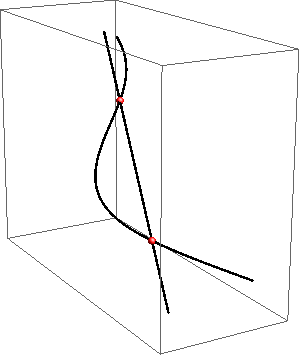
\(^{**}\) Točka u kojoj je sijeku četiri pravca je četverostruka točka raspadnute prodorne krivulje. Ona se računa kao šest dvostrukih točaka. Prostorna krivulja 4. reda može se na više načina raspasti na 4 pravca, ali budući da će se u našim primjerima pojavljivati isključivo ovakvi raspadi (ponekad će četverostruka točka biti beskonačno daleka), ovdje smo kao primjer istakli upravo taj slučaj.
- Red prostorne krivulje invarijanta je projiciranja, odnosno prostorna krivulja \(\small n\)-toga reda projicirat će se u ravninsku krivulju istoga reda
Naime, bilo koji pravac ravnine projekcije možemo smatrati projekcijom neke projicirajuće ravnine. Kako svaka ravnina siječe prostornu krivulju \(\small n\)-toga reda u \(\small n\) točaka i proizvoljno odabrani pravac ravnine projekcije sjeći će ravninsku projekciju te krivulje u \(\small n\) točaka, dakle projekcija prostorne krivulje \(\small n\)-tog reda je ravninska krivulja \(\small n\)-tog reda.
U našim će se primjerima često događati da je ravnina projekcije paralelna s ravninama simetrije ploha u prodoru. Tada će se prostorna prodorna krivulja projicirati u dvostruko brojenu.
Ravninska krivulja može imati više dvostrukih točaka nego prostorna istog reda pa se svaka prostorna krivulja može projicirati u ravninsku krivulju koja od nje ima više dvostrukih točaka. Uočite to svojstvo na gornjim slikama.
Opći princip konstrukcije točaka prodorne krivulje dviju ploha
Opći princip konstrukcije točaka prodorne krivulje dviju ploha sastoji se u tome da prvo odaberemo neki sustav ravnina, a zatim ravninama tog sustava siječemo obje plohe. Svaka ravnina sustava siječe svaku od ploha po nekoj ravninskoj krivulji, a dvije takve krivulje sijeku se u točkama koje su zajedničke za obje plohe. To su točke prodorne krivulje koje leže u promatranoj ravnini.
Sustav ravnina odabiremo tako da su presjeci sa zadanim plohama što jednostavniji te nam omogućuju da što jednostavnijim konstruktivnim postupkom dobijemo dovoljan broj točaka prodorne krivulje. U geometriji ravnala i šestara najpovoljnije su presječne krivulje pravci i kružnice.