Algebarske prostorne krivulje su skupovi točaka prostora čije \(\small (x,y,z)\) koordinate zadovoljavaju dvije algebarske jednadžbe \(\small F_1(x,y,z)=0\) i \(\small F_2(x,y,z)=0\). Takva je krivulja skup točaka koje leže na plohama zadanim tim jednadžbama. Razvrstavamo ih prema njihovu redu (razvrstavaju se i po razredima, ali ćemo takva razmatranja na ovoj razini izostaviti).

  • Red prostorne algebarske krivulje jednak je broju točaka u kojima po volji odabrana ravnina presijeca krivulju.
    Te točke mogu biti realne ili imaginarne.

Teorem

Red prostorne algebarske krivulje koja je prodorna krivulja dviju algebarskih ploha redova \(\small n\) i \(\small m\) je \(\mathbf {n\cdot m}\).\( ^*\)

\( ^*\) Ovdje bi se moglo pogrešno zaključiti da ne postoje algebrske prostorne krivulje čiji je red jednak nekom prim broju, primjerice reda 3.
Takve se krivulje pojavljuju kao dijelovi raspada prodorne krivulje dviju ploha. Za 3. red ćemo kasnije navesti i primjere.

Slika 365: Prostorna krivulja 3. reda
Slika 366: Jednodijelna prostorna krivulja 4. reda
Slika 367: Dvodijelna prostorna krivulja 4. reda

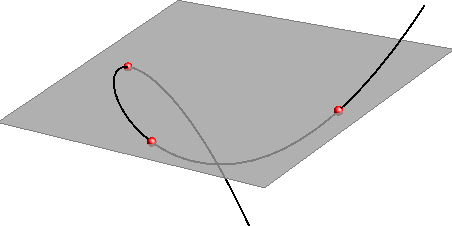
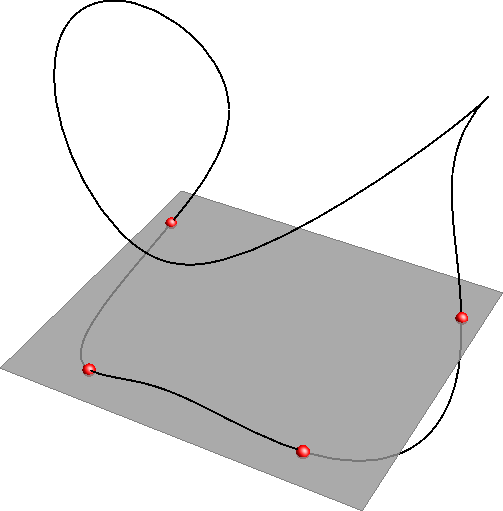
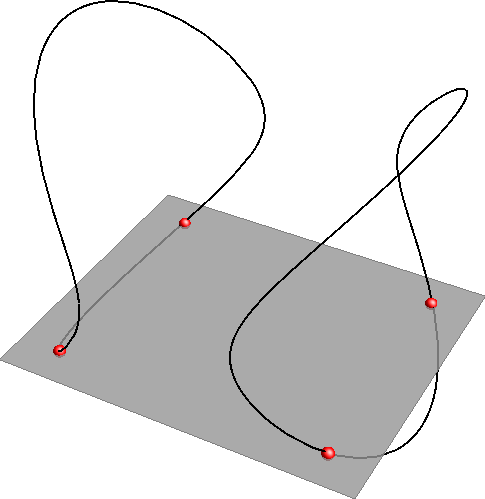
Algebarske prostorne krivulje mogu imati višestruke točke (dvostruke, trostruke...). To su točke kroz koje krivulja više puta prolazi, samu sebe presjeca ili dodiruje. Kao i kod ravninskih krivulja i ovdje je broj dvostukih točaka ograničen i ako krivulja ima veći broj dvostrukih točaka od ”dozvoljenog”, raspada se na krivulje nižih redova.

Maksimalan broj dvostrukih točaka prave prostorne algebarske krivulje \(\small n-\)tog reda je:

  • \(\small \frac{(n-2)^2}{4}\), za \(\small n\) paran
  • \(\small \frac{(n-1)(n-3)}{4}\), za \(\small n\) neparan
Ako krivulja \(\small n-\)tog reda ima više od tog broja dvostrukih točaka, ona se raspada na krivulje nižih redova tako da zbroj redova krivulja u raspadu bude \( \small n\).

Dvostruka točka prodorne krivulje

Neka je \(\small k\) prodorna krivulja ploha \(\small \Phi\) i \(\small \Psi\) i neka je \(\small T\in k\) regularna točka ploha \(\small \Phi\) i \(\small \Psi\).

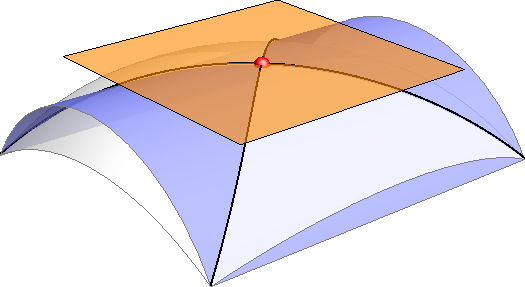
  • Točka \(\small T\) je dvostruka točka krivulje \(\small k\), ako plohe \(\small \Phi\) i \(\small \Psi\) imaju u njoj zajedničku tangencijalnu ravninu (slika 368)
  • Ako je neka točka dvostruka točka plohe, bit će dvostruka točka i svake prodorne krivulje koja kroz nju prolazi (slika 369)

Slika 368
Slika 369

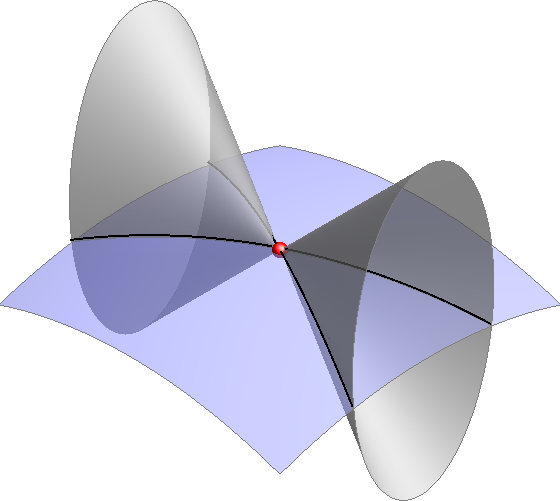
Tangenta prodorne krivulje

Kako dirna ravnina plohe sadrži tangente svih krivulja koje leže na plohi i prolaze tom točkom, možemo zaključiti:

  • Tangenta prodorne krivulje u njenoj regularnoj točki je presječnica dirnih ravnina ploha u toj točki

Vidi animaciju 62.

Animacija 62