Animation below shows this procedure.
Click on the image to start the animation.
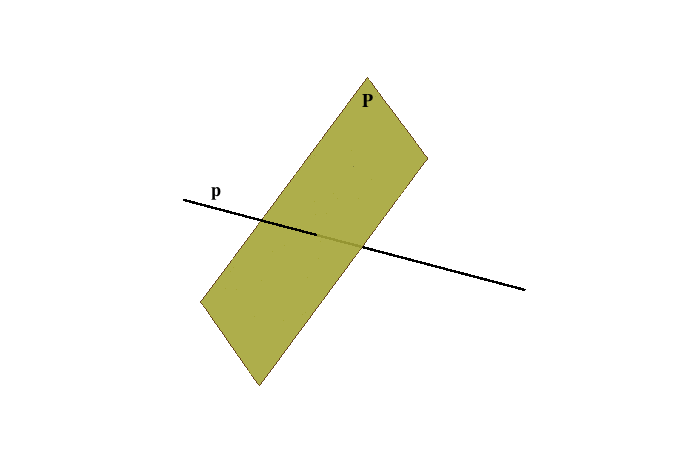
|
1.  Σ , p ⊂ Σ Σ , p ⊂ Σ 2.  f = P ∩ Σ f = P ∩ Σ 3.  P = p ∩ f = p ∩ P P = p ∩ f = p ∩ P |

 1. Intersection of a straight line and a plane using a plane
in general position as auxiliary plane.
1. Intersection of a straight line and a plane using a plane
in general position as auxiliary plane.

 2. Intersection of a straight line and a plane using a projecting plane as auxiliary plane.
2. Intersection of a straight line and a plane using a projecting plane as auxiliary plane.
The comparison of the two given constructions are presented in the figures below. Because of the simplicity of the second approach we will always use projecting planes as auxiliary planes in the construction
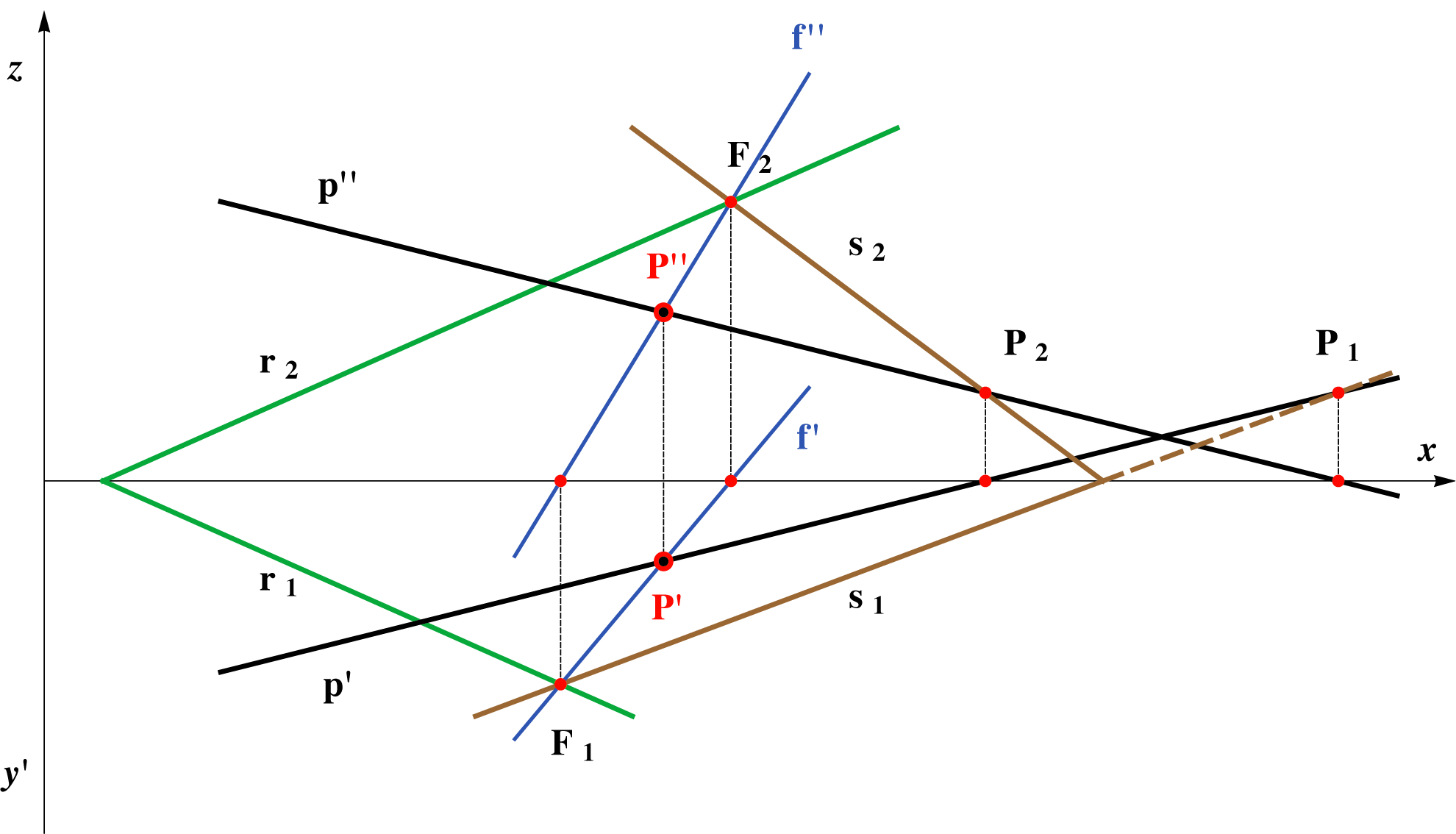
|
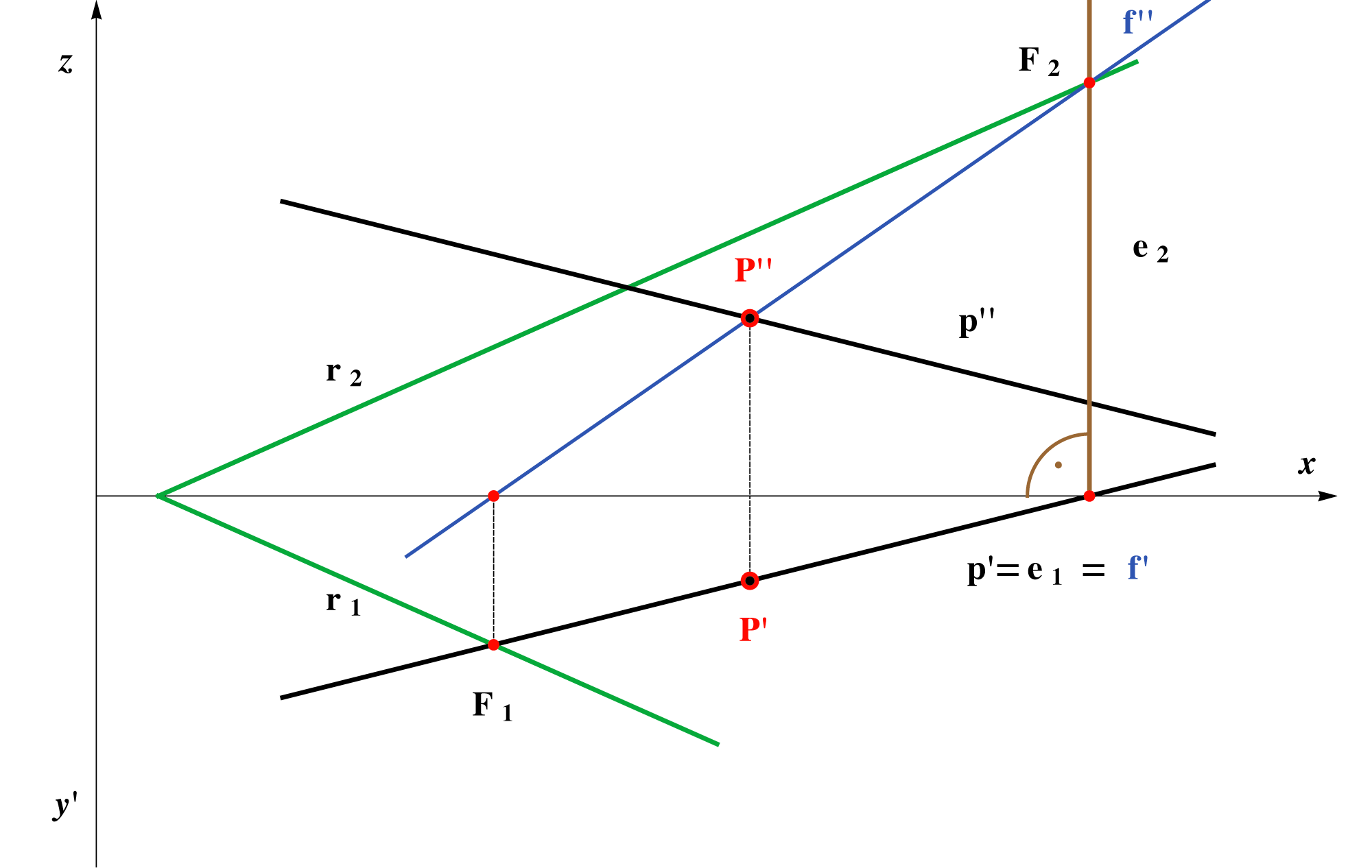
|
|
Auxiliary plane Σ is an oblique plane. |
Auxiliary plane E is a projecting plane. |
Assignment 1: Construct the projections of the point of intersection of the line p=AB[A(0,4,3);B(6,–1,–1)] with the plane P(∞,3,2).




 As
an axiliary plane use the vertical projecting plane E.
As
an axiliary plane use the vertical projecting plane E.




 Denote
the visibility of p with regard to the plane P in both projections.
Denote
the visibility of p with regard to the plane P in both projections.
Assignment 2: Construct the projections of the point of intersection of the line a=A1A2[A1(5,3,0);A2(–1,0,4)] Δ(3,2,–3).




 As
an axiliary plane use the horizontal projecting plane E.
As
an axiliary plane use the horizontal projecting plane E.




 Denote
the visibility of p with regard to the plane Δ in both projections.
Denote
the visibility of p with regard to the plane Δ in both projections.
The intersection of a straight line with a projecting plane
When we are dealing with projecting planes, we must remember that they are perpendicular to one (or more) planes of projection, and in that projection they project onto a line (corresponding trace). Therefore, that projection of the intersection of a line and that plane also lies on that trace. See the images below.
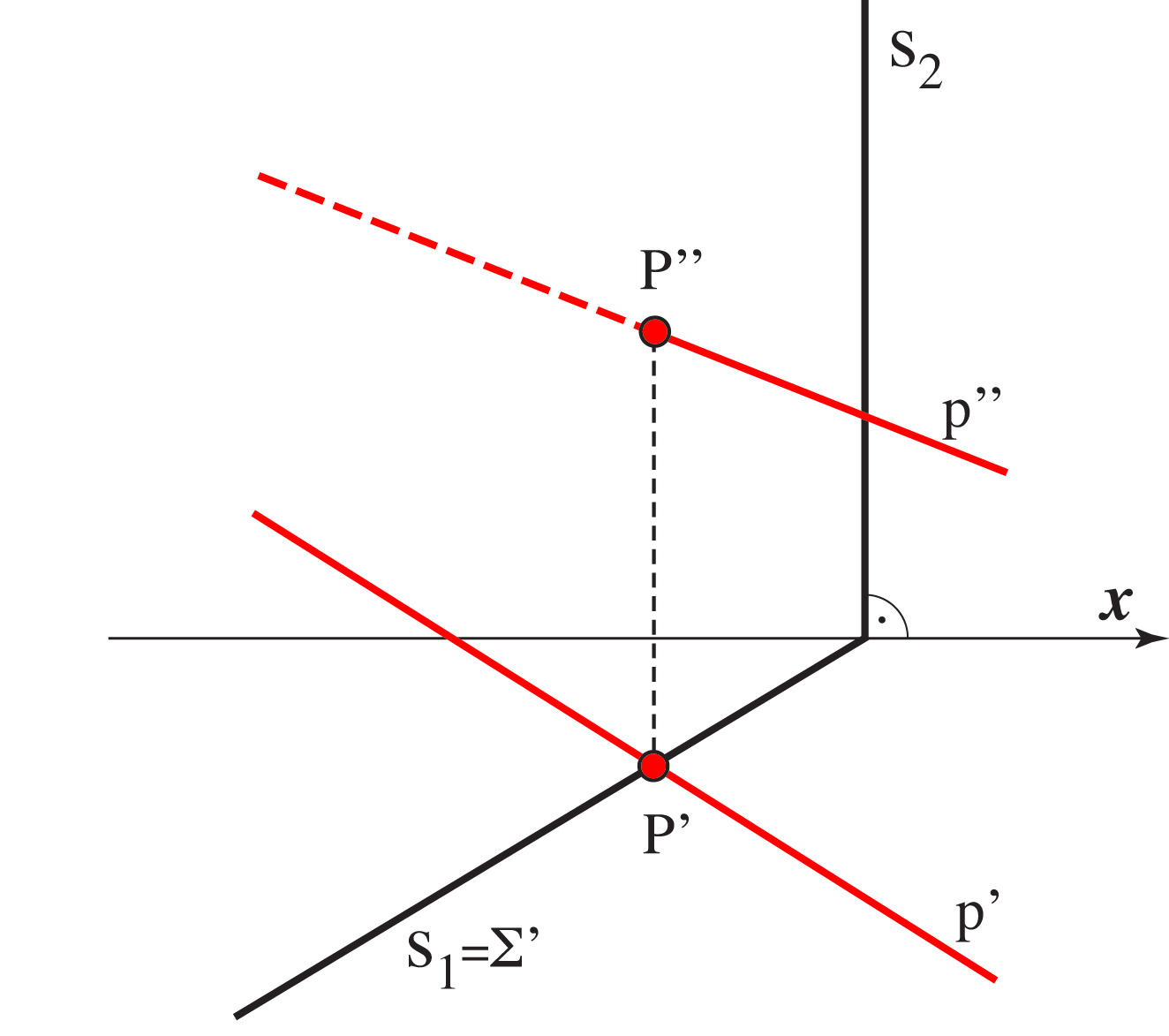
|

|
|
Construction of the intersection of the line p with horizontal projecting plane Σ. |
Construction of the intersection of the line p with vertical projecting plane Σ. |
Created by Sonja Gorjanc, translated by Helena Halas and Iva Kodrnja - 3DGeomTeh - Developing project of the University of Zagreb