The right angle (and all other angles) will be projected in true size if its sides are parallel to the plane of projection.
The following holds for the right angle:
Proof of this statement can be seen on the image below.
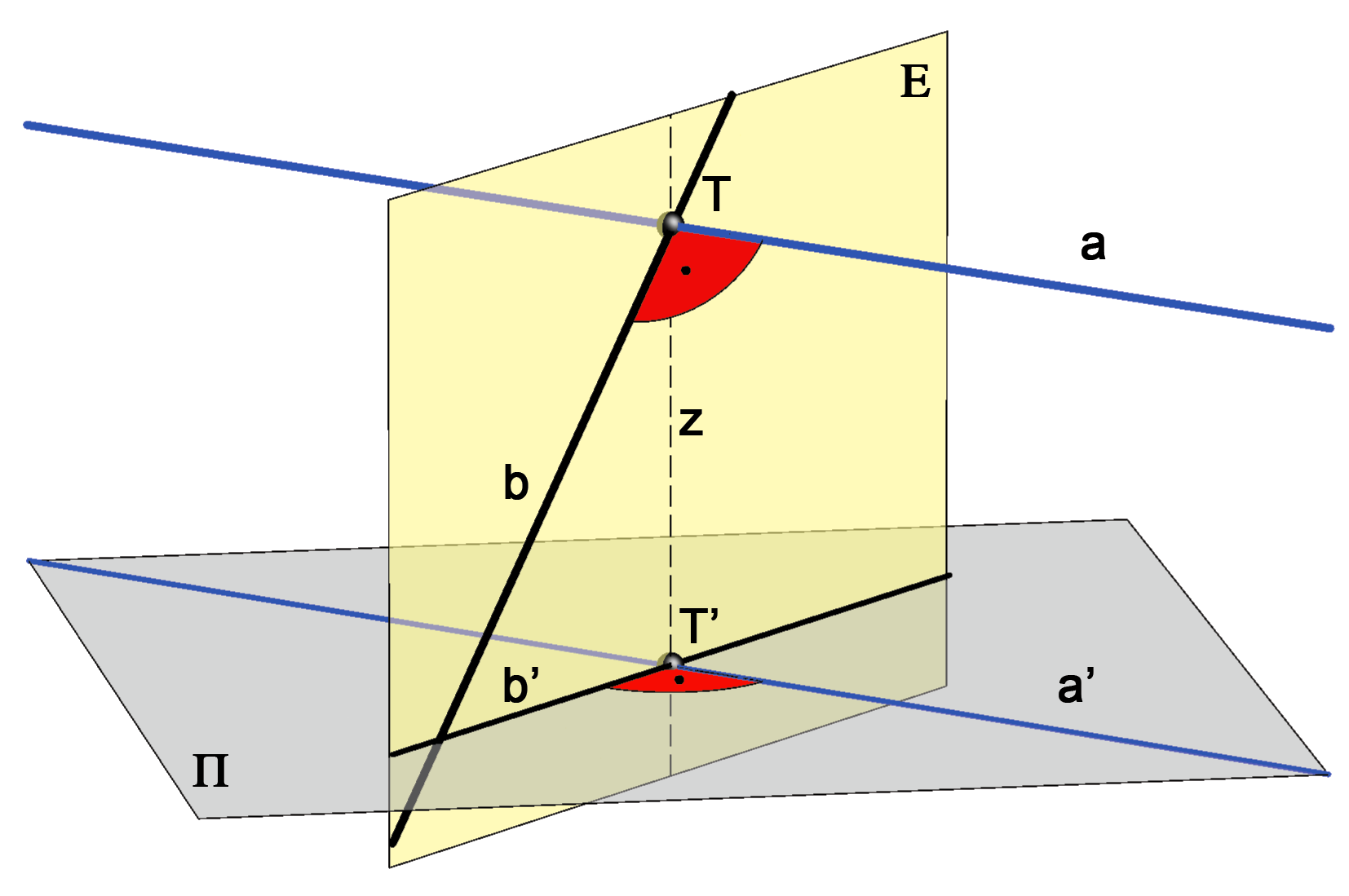
|
A line a is parallel to the plane of projection Π
and perpendicular to the line b. We need to prove that
their projections are also perpendicular, i.e. a' ⊥ b'. (Line a is parallel to the plane Π, while z is perpendicular to Π.) Proof can be written as: a ⊥ b & a | | Π  => =>  a ⊥ E a ⊥ E  => =>  a' ⊥ E a' ⊥ E  => =>  a' ⊥ b'. a' ⊥ b'.
|
Straight line and a plane perpendicular to each other
Any line n perpendicular to the plane P is called a normal line of the plane P and their point of intersection, N = n ∩ P is called pedal (perpendicular foot) of the line n.
n ⊥ P <=>
<=> p' ⊥ r1 & p'' ⊥ r2.
p' ⊥ r1 & p'' ⊥ r2.
This claim follows from the fact that a line perpendicular to a plane must be perpendicular to all lines contained in that plane, also to its traces. Since the line is perpendicular to the horizontal trace r1 (r2) that belongs to the plane Π1 (Π2), horizontal (vertical) projection of this angle will be in true size - right angle.
The image below shows this statement and also shows those principal lines of the plane that intersect the normal line in its pedal point.
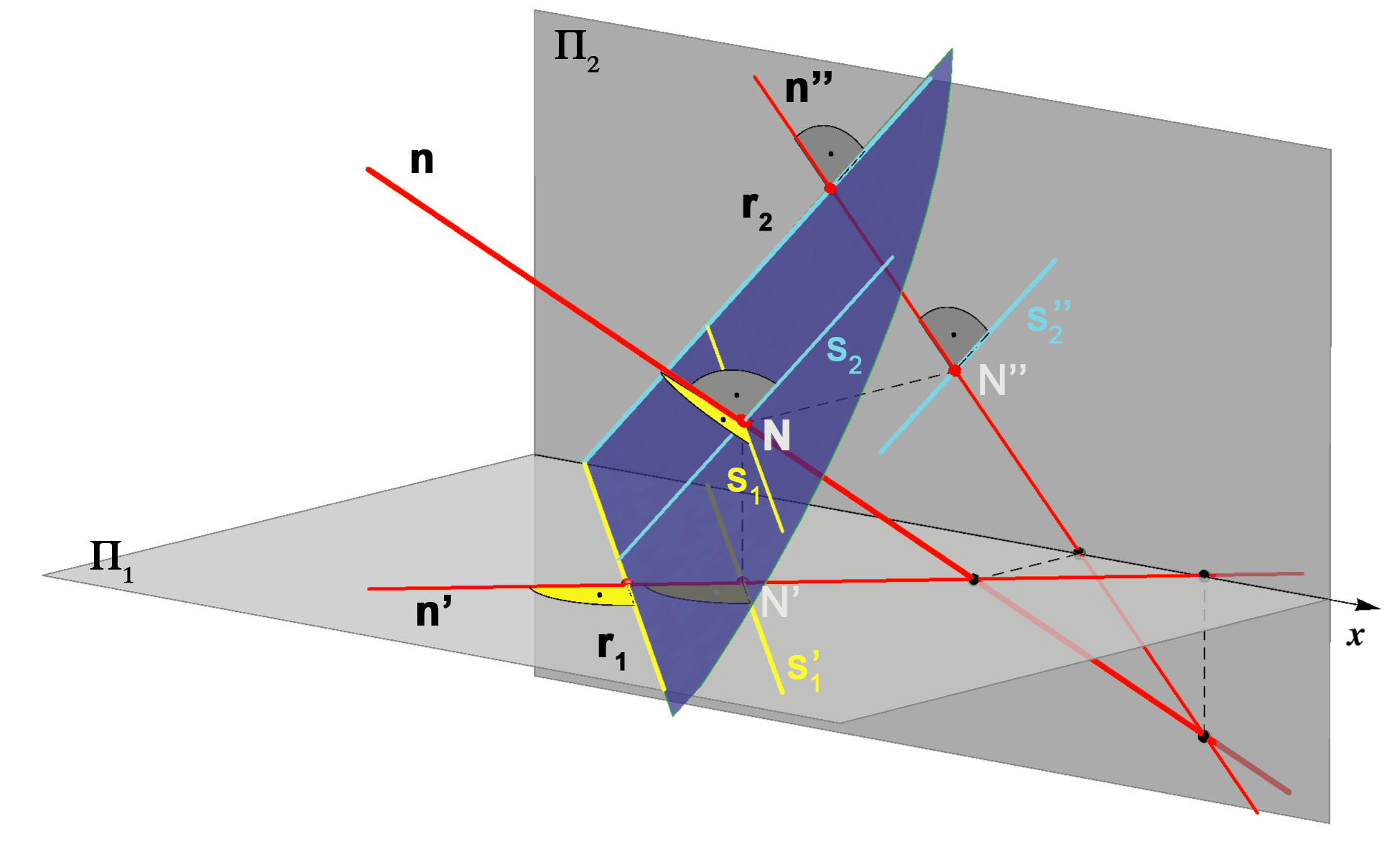
|
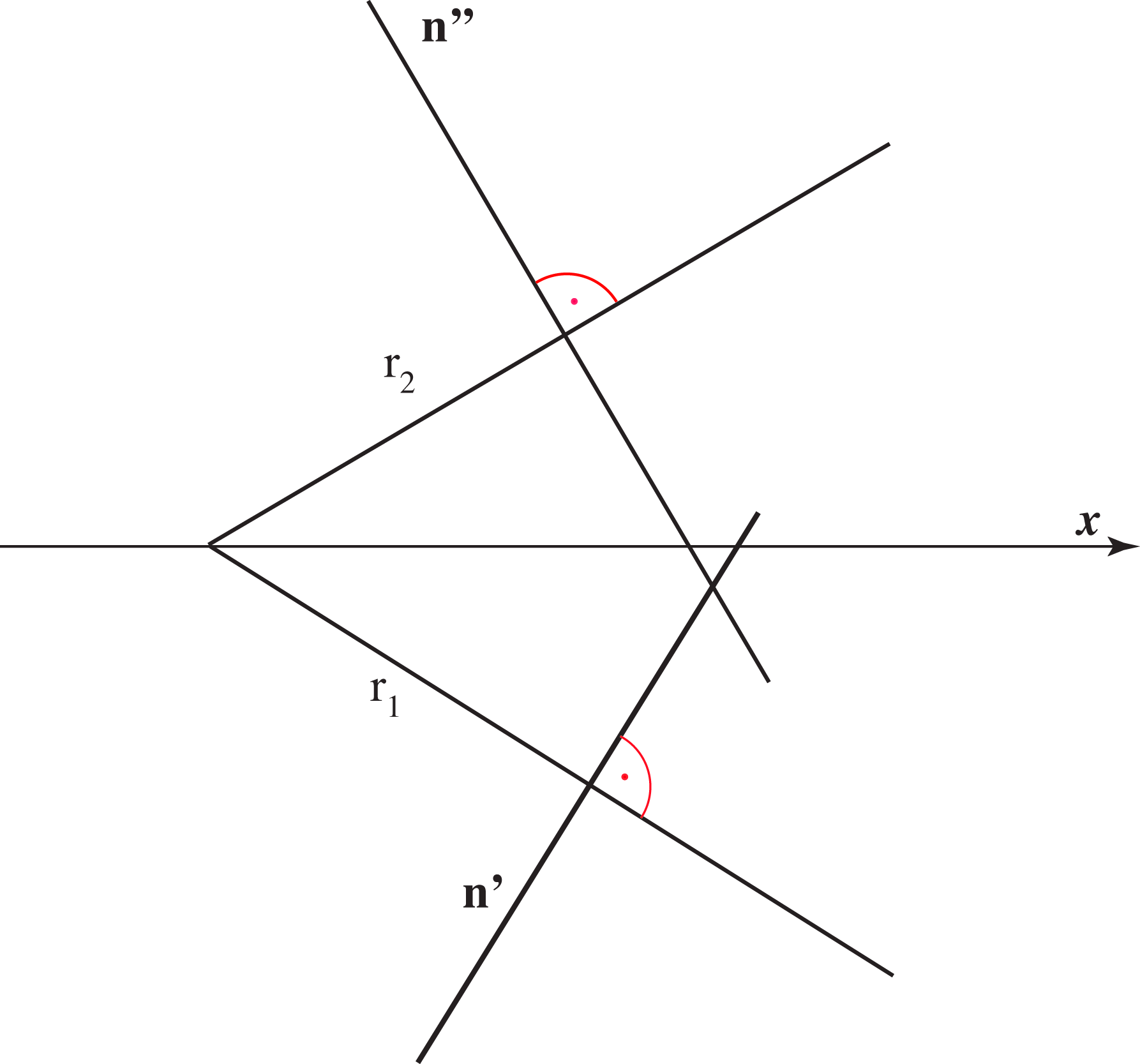
|
Assignment 1: Construct the projections of a line that passes through the given point and it is perpendicular to the plane given by its traces.
Assignment 2: Construct the traces of a plane that passes through the given point and it is perpendicular to the given line.
Assignment 3: Determine the distance of a given point and a given plane (plane is given by its traces).
Assignment 4: Determine the distance between a given point and a given line.
Bisector plane of a line segment
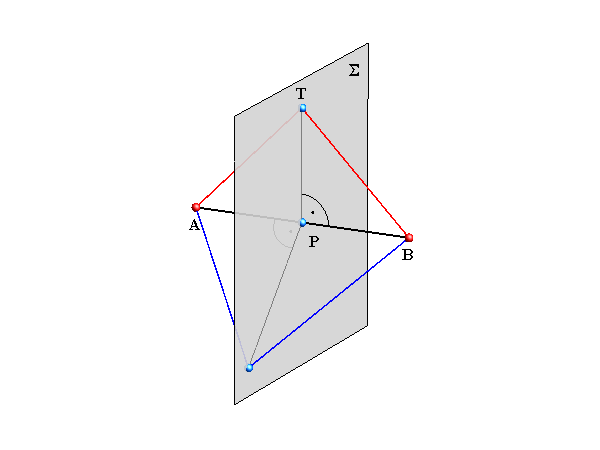
T ∈ Σ  <=> <=> d(A,T) = d(B,T) d(A,T) = d(B,T)
|
|
Assignment 5: Construct the traces of the bisector plane of a given line segment.
True length of the normal line
Let n be the normal line of the plane P and N their intersection point.Let p1 be the 1st steepest line of the plane P that passes through the point N, and p2 the 2nd steepest line that passes through N.
Due to the property of orthogonal projection of the right angle mentioned before (n' ⊥ r1, n'' ⊥ r2), lines n and p1 will have the same top view (n' = p'1) and the lines n and p2 will have the same front view (n'' = p''2).
Therefore, the lines n and p1 lie in the same horizontal projecting plane and the lines n and p2 lie in the same vertical projecting plane.
These properties are shown in the images below.
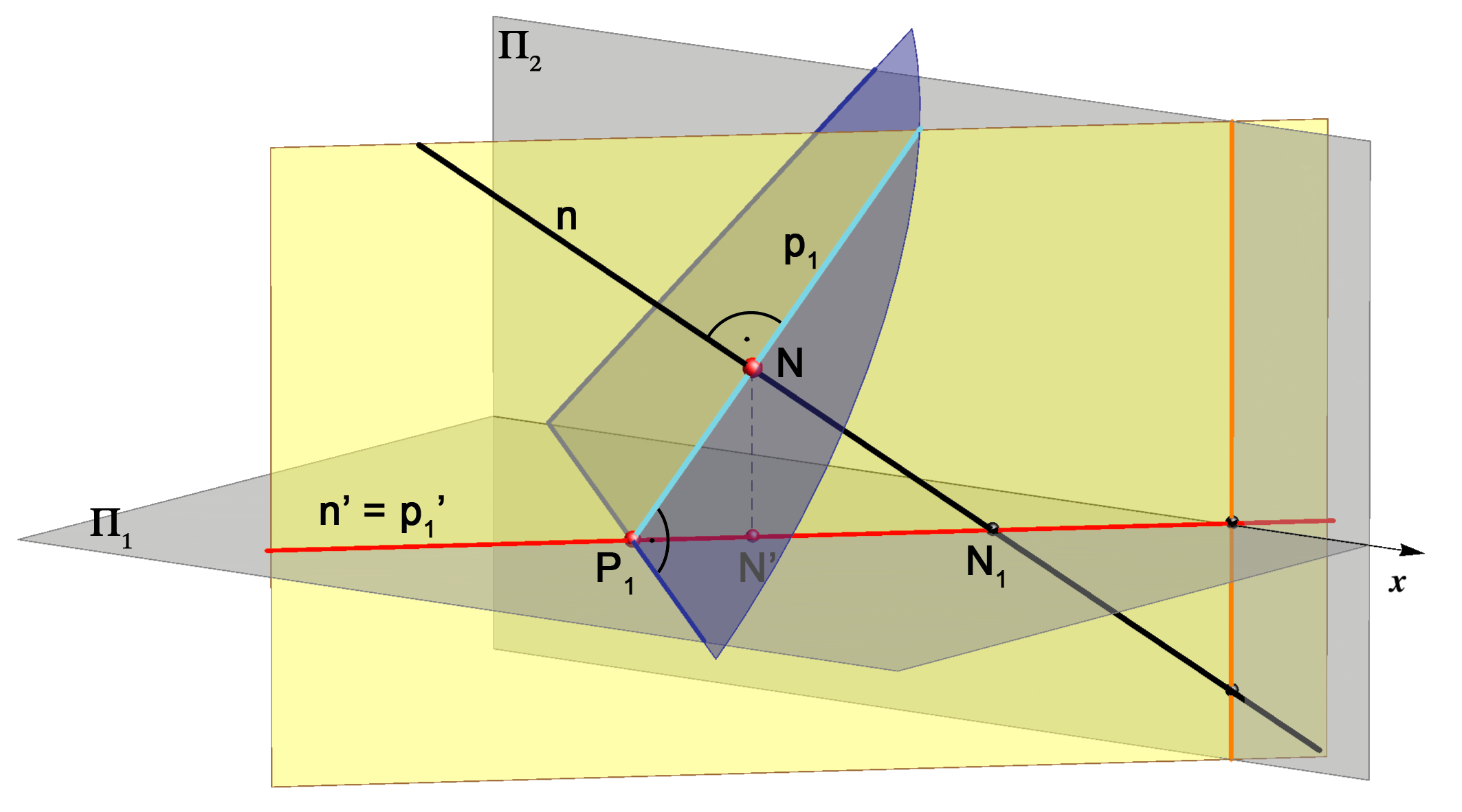
|
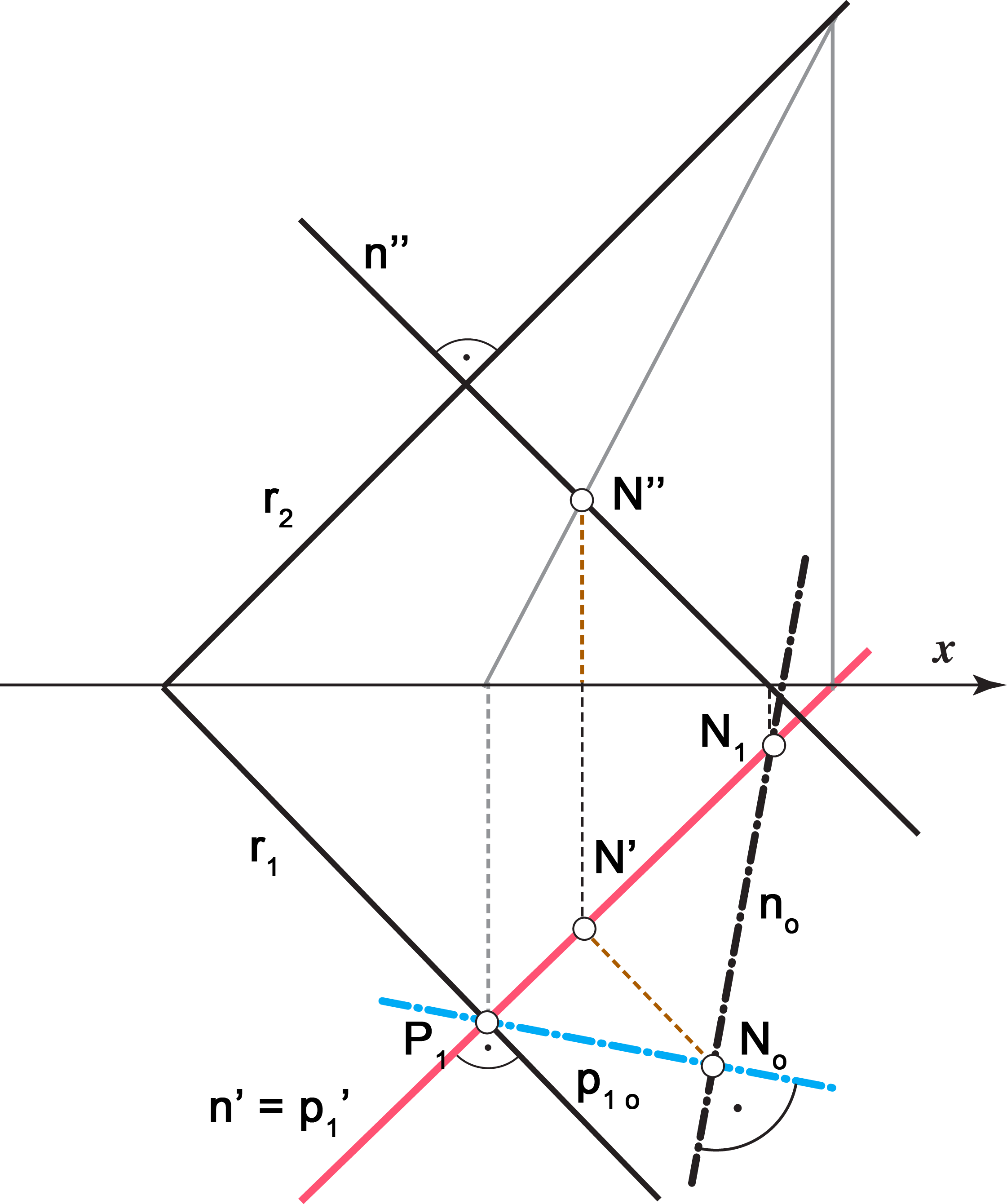
|
| The normal line and the1st steepest line through the pedal of the normal lie in the same horizontal projecting plane. | The normal line rotated into the plane Π1 is perpendicular to the 1st steepest line rotated as well, they intersect at the projection of the pedal. |
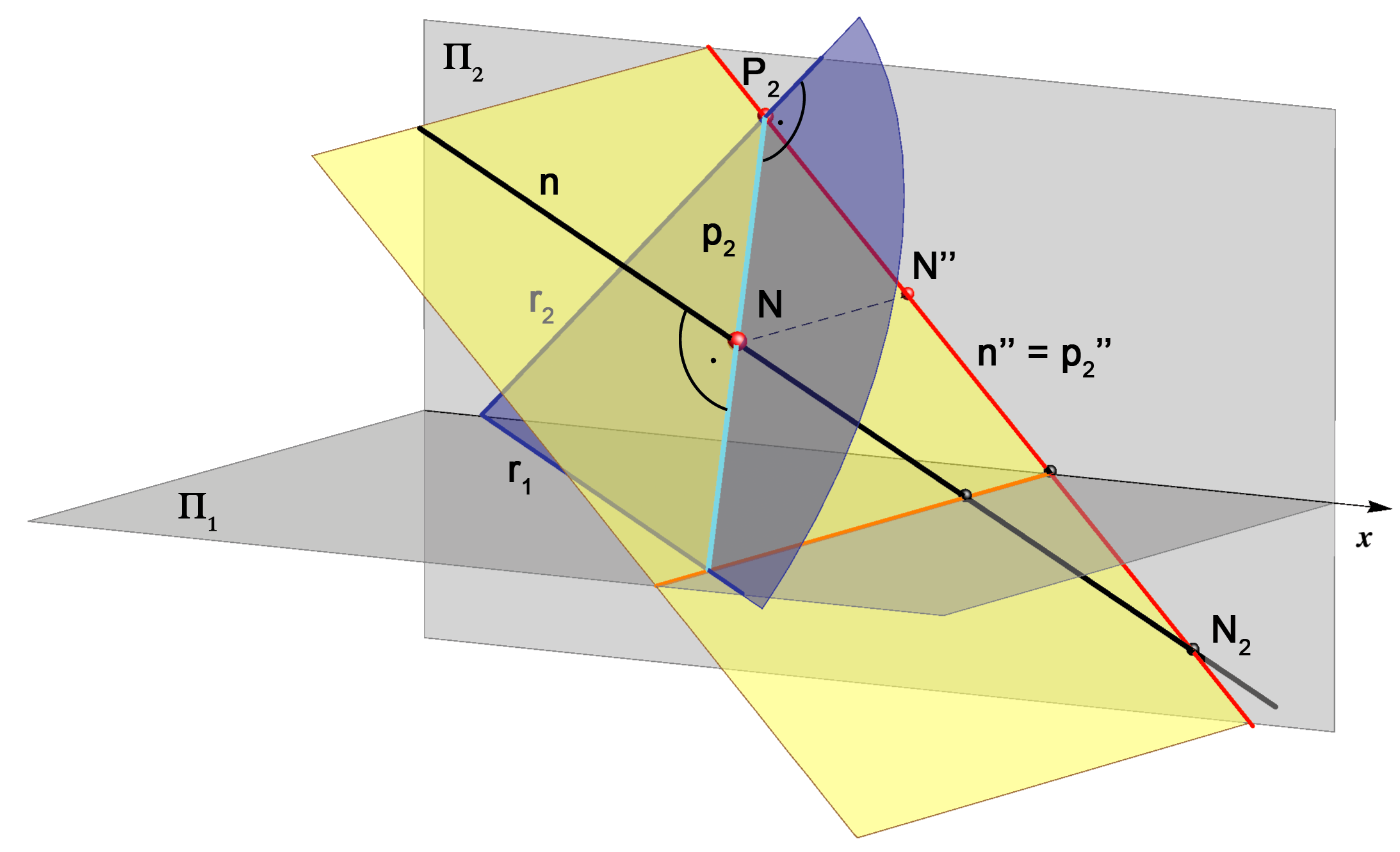
|
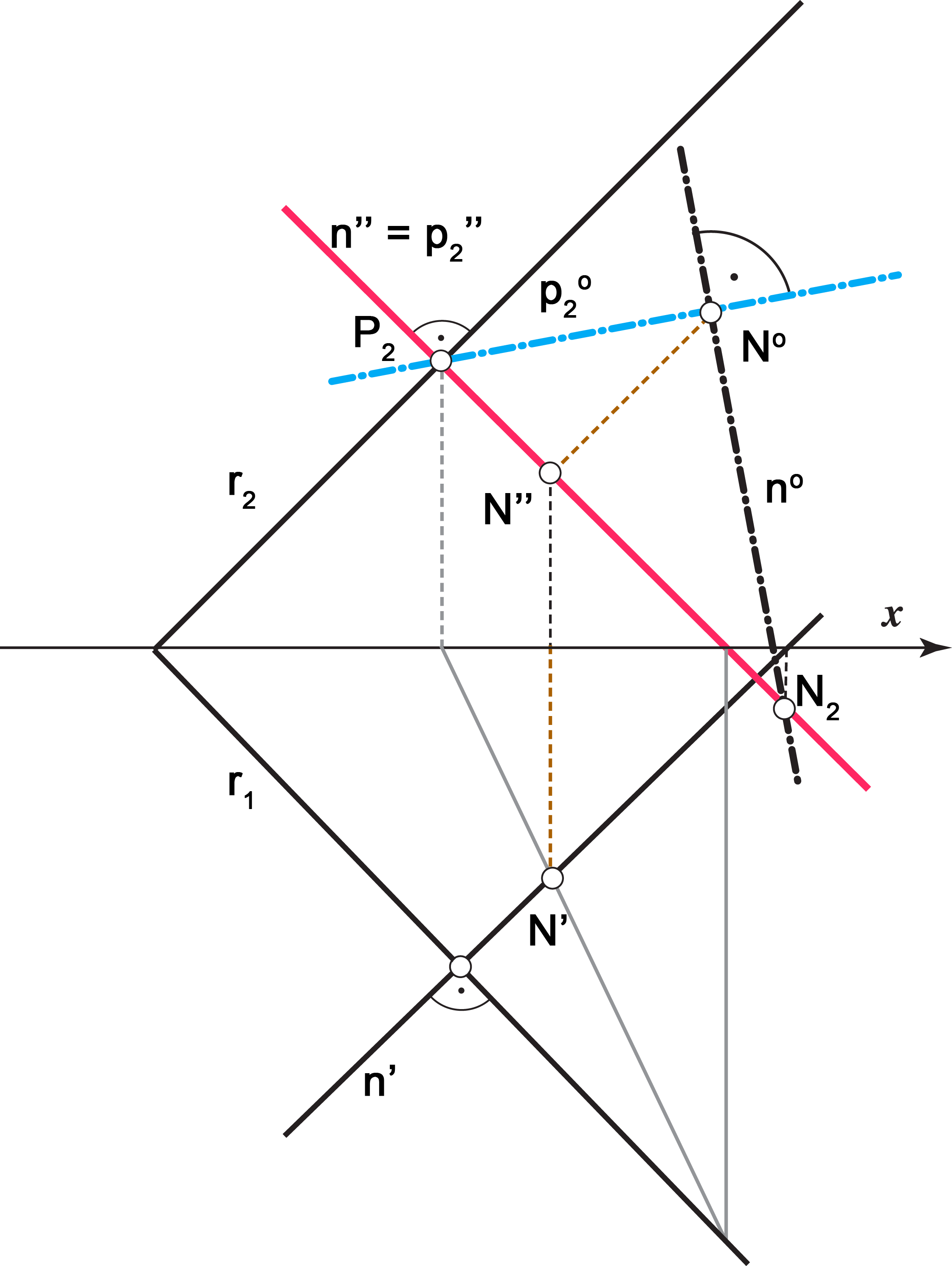
|
| The normal line and the 2st steepest line through the pedal of the normal lie in the same vertical projecting plane. | The normal line rotated into the plane Π2 is perpendicular to the 2st steepest line rotated as well, they intersect at the projection of the pedal. |
Assignment 6: Lay a line through the point T(1,3,–) that is perpendicular to the plane P(–3,4,3) and has length 4.