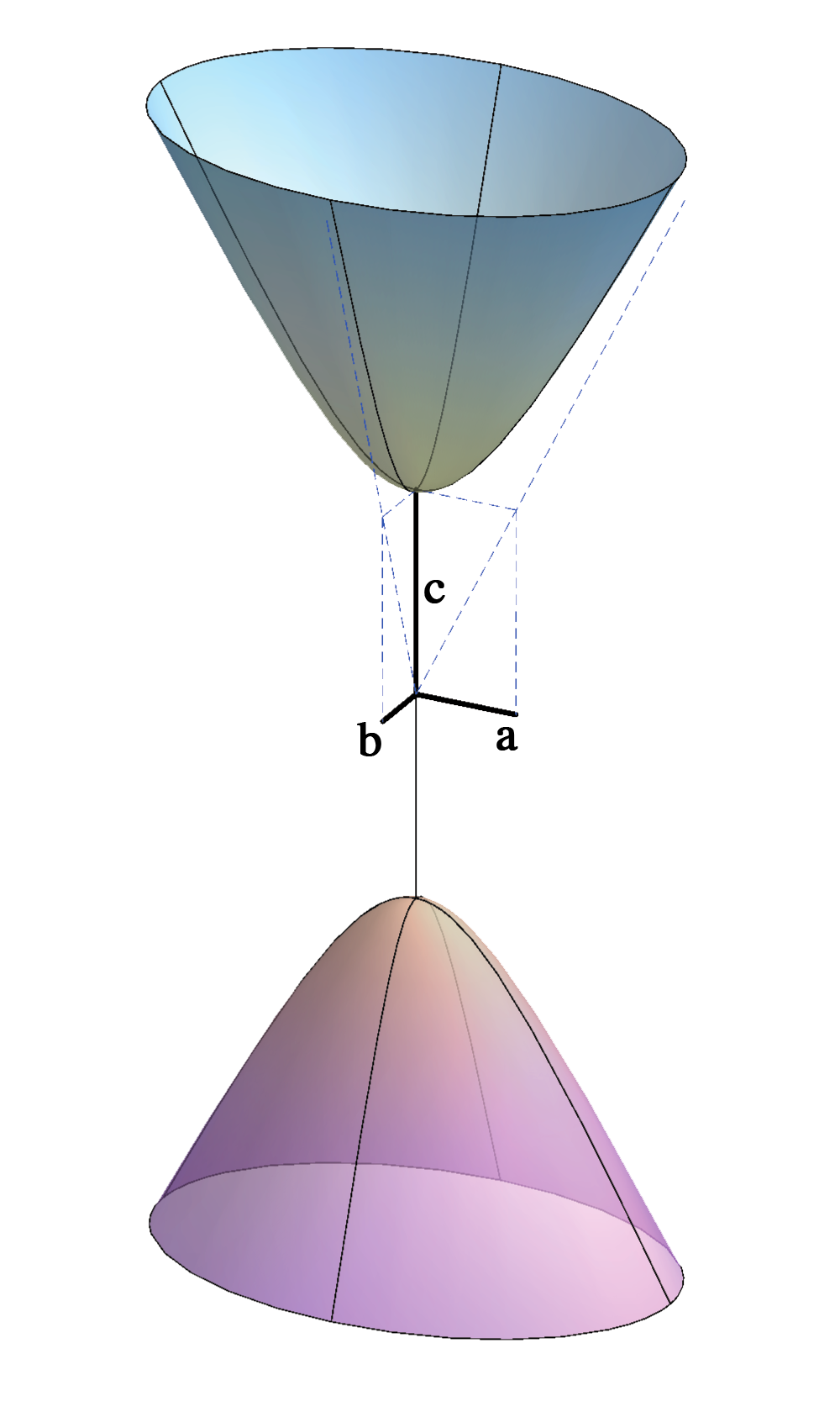
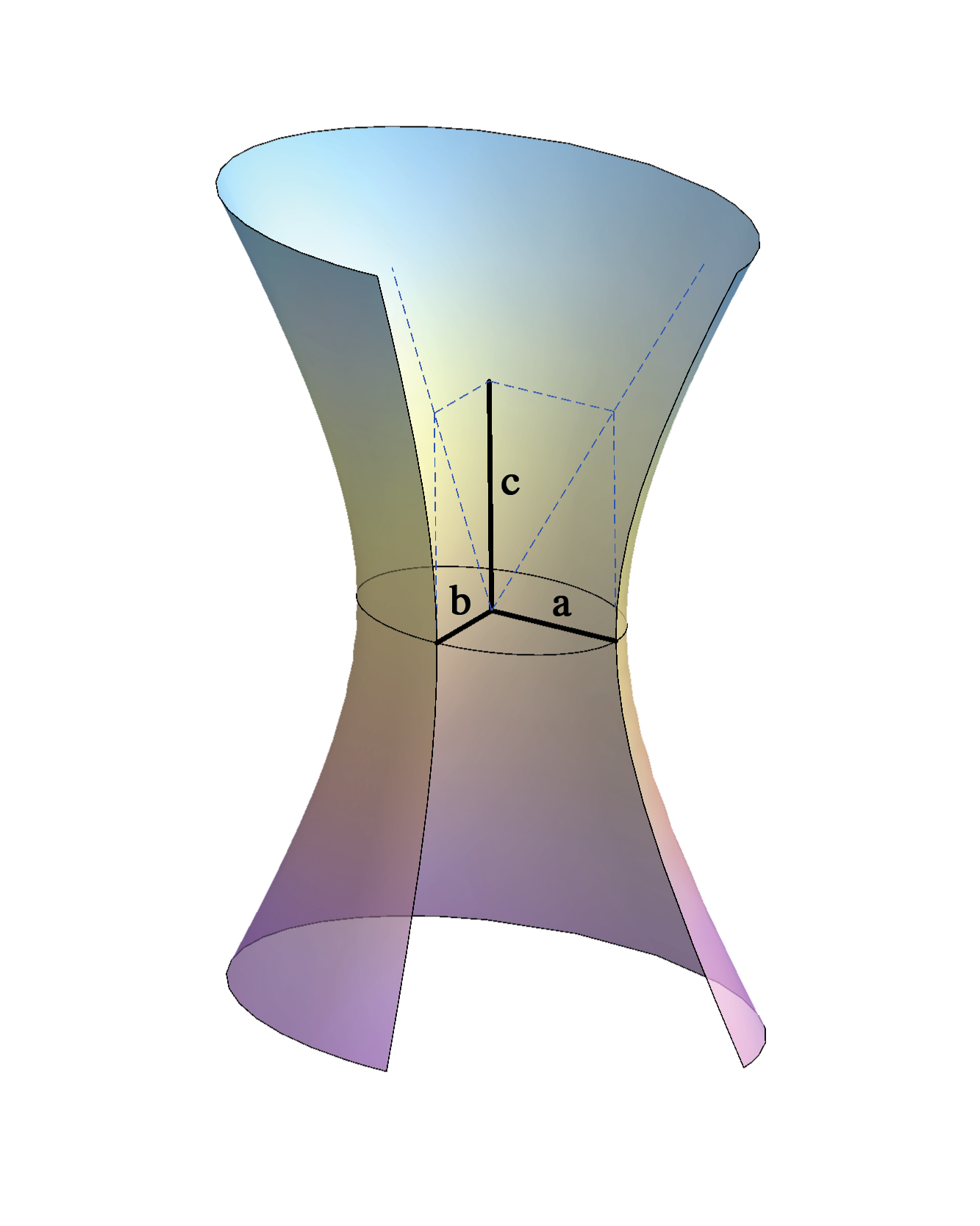
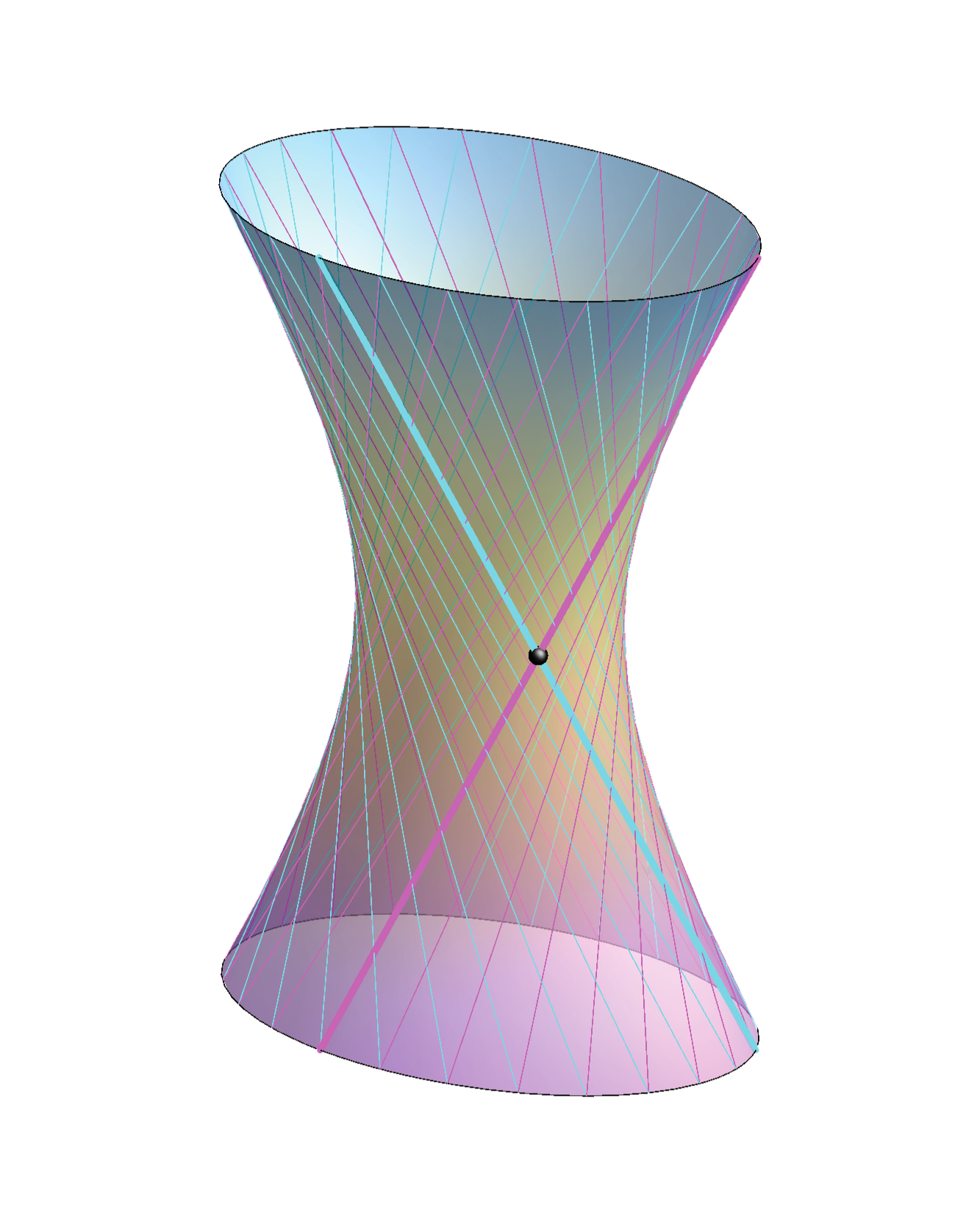
\(-\frac{x^2}{a^2}-\frac{y^2}{b^2}+\frac{z^2}{c^2}=1\)
Real plane intersections are:
the ellipses, the circles, the parabolas and the hyperbolas.
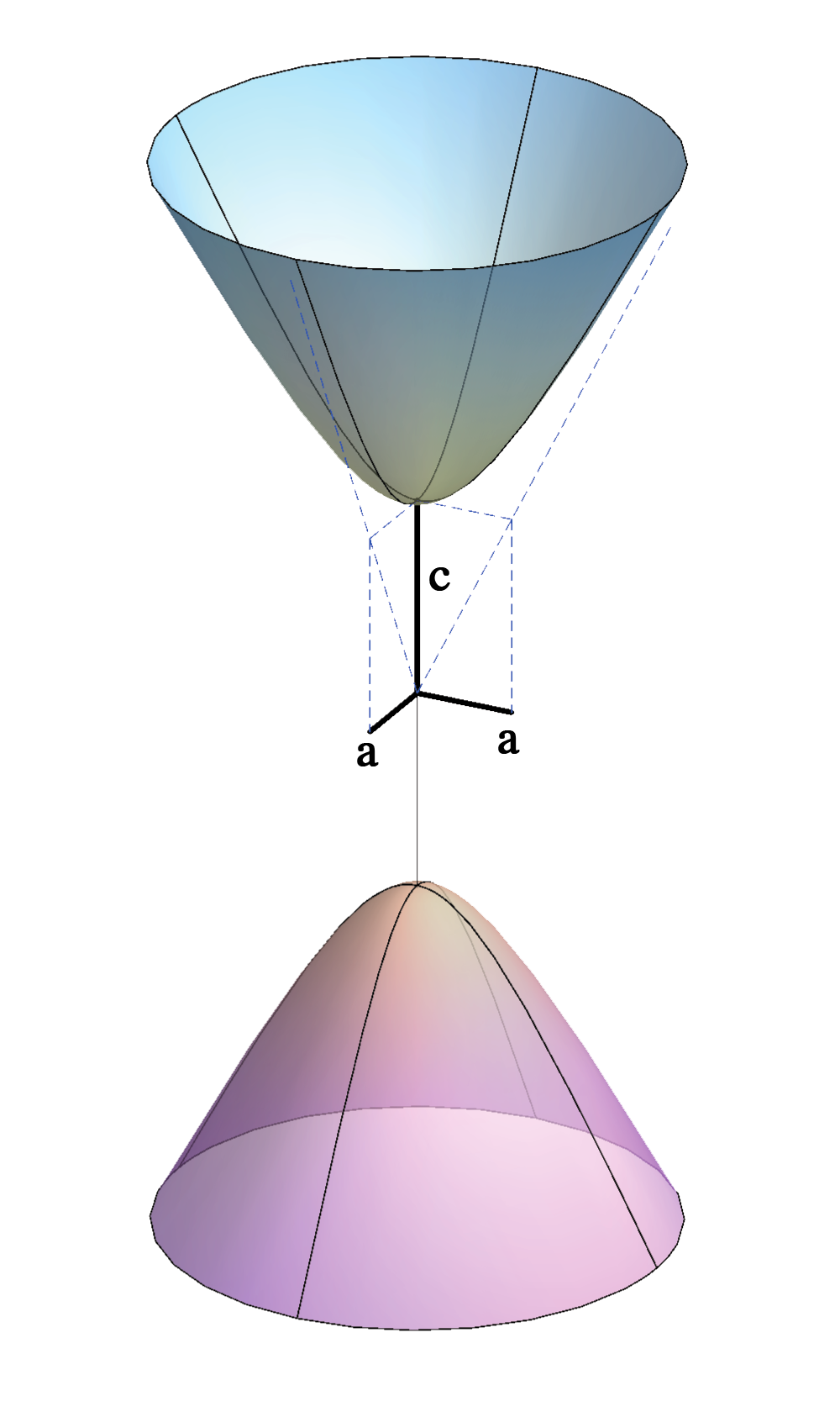
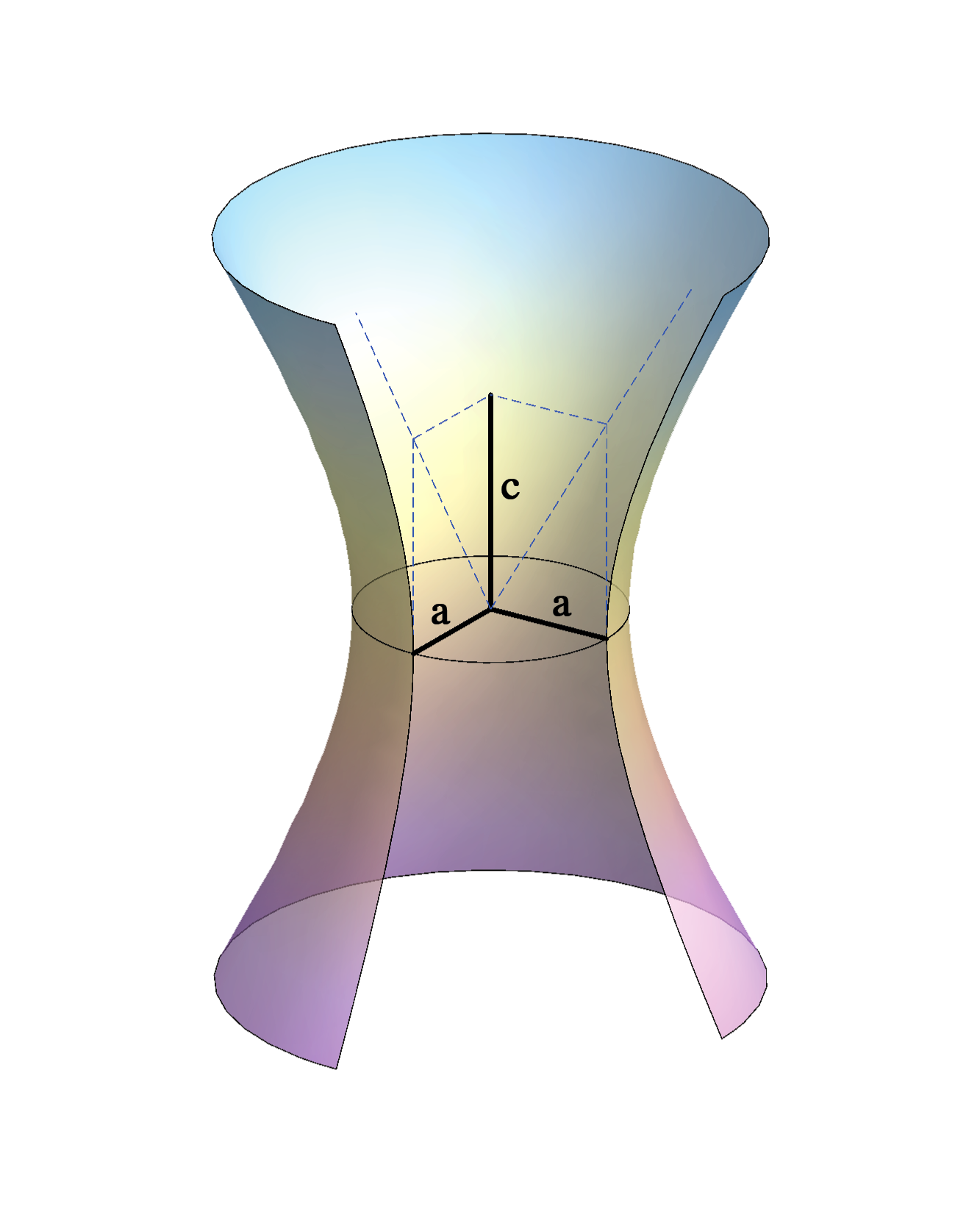
\(-\frac{x^2}{a^2}-\frac{y^2}{a^2}+\frac{z^2}{c^2}=1\)
It is obtained by rotating a hyperbola about its transverse axis.
Real plane intersections are:
the ellipses,the circles, the parabolas and the hyperbolas.