Primjer 5.

Na zadanom nosaču analitičkim postupkom odrediti dijagrame momenata i poprečnih sila.

Prvi je korak u rješavanju zadatka određivanje ležajnih reakcija, koje izračunavamo postavljanjem jednadžbi ravnoteže za cijeli nosač. Pritom zadano distribuirano opterećenje zamjenjujemo njegovom rezultantom. Iznos rezultante jednak je površini trokutnog opterećenja, Q = ${\frac{{1}}{{2}}}$ q₀^.l. Rezultanta prolazi težištem trokuta, x_T(Q) = ${\frac{{2}}{{3}}}$ l.

Reakciju $\vec{{A}}$ rastavljamo na horizontalnu i vertikalnu komponentu. Jednadžbe ravnoteže daju:

$\displaystyle \sum$ F_x	= 0 $\displaystyle \Rightarrow$ A^h = 0,
$\displaystyle \sum$ M_B	= 0 $\displaystyle \Rightarrow$ - A^{v .}l + Q^. $\displaystyle {\frac{{l}}{{3}}}$ = 0 $\displaystyle \Rightarrow$ A^v = $\displaystyle {\frac{{q_0 l}}{{6}}}$ ,
$\displaystyle \sum$ M_A	= 0 $\displaystyle \Rightarrow$ B^{v .}l - Q^. $\displaystyle {\frac{{2l}}{{3}}}$ = 0 $\displaystyle \Rightarrow$ B^v = $\displaystyle {\frac{{q_0 l}}{{3}}}$ .

Uz poznate vrijednosti reakcija, presijecanjem nosača u proizvoljnoj točki možemo iz jednadžbi ravnoteže dijela nosača izračunati vrijednosti unutarnjih sila. U te jednadžbe ulaze reakcije, rezultanta dijela zadanog distribuiranog opterećenja na promatranom dijelu nosača te unutarnje sile. Iznos rezultante jednak je površini sudjelujućega dijela opterećenja,

Q(x) = q(x) $\displaystyle {\frac{{x}}{{2}}}$ = q₀ $\displaystyle {\frac{{x^2}}{{2l}}}$ ,

M(x)	= A^{v .}x - Q(x)^. $\displaystyle {\frac{{x}}{{3}}}$ = $\displaystyle {\frac{{q_0 l}}{{6}}}$ - $\displaystyle {\frac{{q_0 x^2}}{{2l}}}$ ^. $\displaystyle {\frac{{x}}{{3}}}$ = $\displaystyle {\frac{{q_0 x}}{{6l}}}$ $\displaystyle \left(\vphantom{ l^2 - x^2 }\right.$ l² - x² $\displaystyle \left.\vphantom{ l^2 - x^2 }\right)$ ,
T(x)	= - A^v + Q(x) = - $\displaystyle {\frac{{q_0 l}}{{6}}}$ + $\displaystyle {\frac{{q_0 x^2}}{{2l}}}$ = $\displaystyle {\frac{{q_0}}{{6l}}}$ $\displaystyle \left(\vphantom{ 3x^2 - l^2 }\right.$ 3x² - l² $\displaystyle \left.\vphantom{ 3x^2 - l^2 }\right)$ ,
N(x)	= - A^h = 0.

Položaj maksimalnog momenta dobivamo iz uvjeta 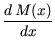${\dfrac{{d M(x)}}{{dx}}}$ = - T(x) = 0, te je x_max = l $\sqrt{{3}}$ /3, a M_max = q₀ l² $\sqrt{{3}}$ /27.

Momentni dijagram, kubnu parabolu, konstruirat ćemo rekurzivno, sve točnijom aproksimacijom distribuiranog opterećenja koncentriranim silama.

U prvom koraku opterećenje zamjenjujemo rezultantom $\vec{{Q}}$ . Moment ispod sile $\vec{{Q}}$ (moment u `šiljku' momentnog dijagrama) jest

M( $\displaystyle {\tfrac{{2}}{{3}}}$ l )= A^{v .} $\displaystyle {\frac{{2}}{{3}}}$ l = $\displaystyle {\frac{{Q}}{{3}}}$ ^. $\displaystyle {\frac{{2}}{{3}}}$ l = $\displaystyle {\frac{{q_0 l^2}}{{9}}}$ .

U drugom koraku opterećenje zamjenjujemo dvjema silama, $\vec{{Q}}_{1}^{}$ i $\vec{{Q}}_{2}^{}$ , koje su rezultantne segmenata lijevo (trokut) i desno (trapez) od pravca djelovanja rezultante $\vec{{Q}}$ . Momentni će dijagram sada imati dva `šiljka'. Vrijednosti u tim točkama, međutim, ne trebamo računati. Promatramo li gredu u cjelini, te su dvije rezultante po djelovanju ekvivalentne trokutnom opterećenju, a time i rezultanti $\vec{{Q}}$ , pa su reakcije jednake u oba slučaja. To znači da su i momenti u svim presjecima od ležaja A do hvatišta sile $\vec{{Q}}_{1}^{}$ te od ležaja B do hvatišta sile $\vec{{Q}}_{2}^{}$ jednaki onima iz prethodnog koraka, drugim riječima, odsječci momentnog dijagrama za te dijelove grede i sada leže na pravcima 0 i 1. Srednji je odsječak dijagrama na pravcu 2 koji prolazi sjecištima pravaca 0 i 1 s pravcima djelovanja sila $\vec{{Q}}_{1}^{}$ i $\vec{{Q}}_{2}^{}$ . I pravac 2 tangenta je na konačni dijagram. Diralište je sjecište tog pravca s pravcem koji razdvaja segmente opterećenja (pravac djelovanja sile $\vec{{Q}}$ ); naime, upravo je u presjeku na tom pravcu moment rezultante $\vec{{Q}}_{1}^{}$ jednak momentu odgovarajućega trokutnog segmenta distribuiranog opterećenja (i, naravno, s druge strane, moment sile $\vec{{Q}}_{2}^{}$ jednak momentu odgovarajućeg trapeznog segmenta).

Postupak možemo nastaviti do željene točnosti. U svakom koraku segmente iz prethodnoga koraka pravcima djelovanja pripadnih rezultanti dijelimo na po dva segmenta koje ponovo zamjenjujemo rezultantama. Spojnice sjecišta novih rezultanti i u prethodnim koracima dobivenih tangenti daju nove tangente.

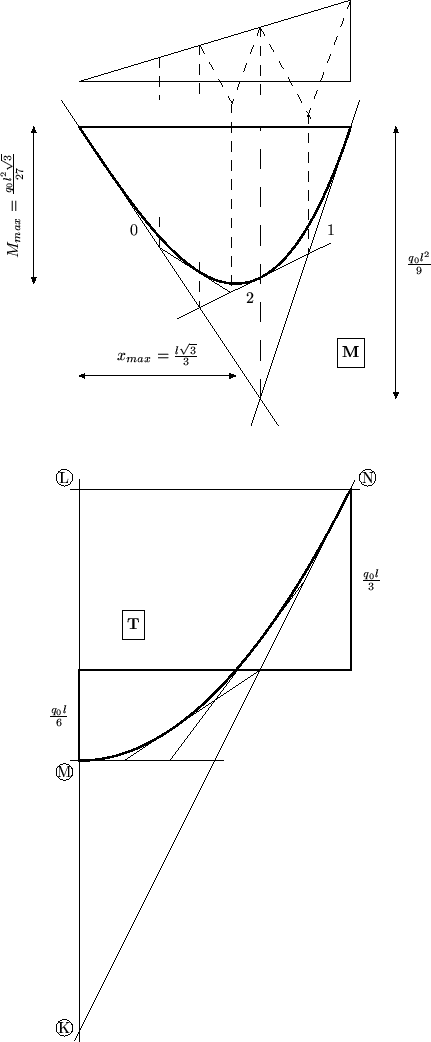
Pri konstrukciji dijagrama poprečnih sila primijenit ćemo neka, iz Nacrtne geometrije poznata, svojstva parabole kao krivulje drugog reda i drugog razreda.

Vrijednosti poprečnih sila u točkama A i B (točnije, neposredno desno od točke A i neposredno lijevo od B) poznate su: T_A^d = - A, T_B^l = B. Tako dobivamo točke M i N parabole. Iz poznatoga diferencijalnog odnosa ${\frac{{d T(x)}}{{dx}}}$ = - q(x) slijedi da je tangenta na parabolu u točki M horizontalna. Kako je parabola simetrična u odnosu na vertikalu kroz točku M (tj. os y), bit će taj pravac os parabole, a točka M njezino tjeme. (Podsjetimo da je beskonačno daleka točka osi parabole diralište njene beskonačno daleke tangente. Dovoljan broj točaka parabole mogli bismo sada konstruirati projektivnim pridruživanjem pramenova pravaca kojima su vrhovi tjeme M i beskonačno daleka točka osi. Mi ćemo, međutim, parabolu konstruirati kao proizvod projektivnih nizova, odnosno, kao i kod momentnog dijagrama, konstruirat ćemo tangentni poligon.)

Tangente parabole sijeku dvije njene odabrane (ili zadane) tangente u sličnim nizovima. Potrebna nam je, prema tome, još tangenta u točki N. Znamo da je udaljenost od nožišta L okomice iz točke N na os parabole do tjemena jednaka udaljenosti od tjemena do sjecišta K tangente u točki N i osi, d (L, M) = d (M, K), pa traženu tangentu možemo lako konstruirati. Zadajmo sada na tjemenoj tangenti i na tangenti u točki N slične nizove tako da odsječke tih tangenata između njihovih dirališta i njihovoga sjecišta podijelimo na jednaki broj dijelova; spojnice pridruženih točaka tih dvaju nizova omataju parabolu.