Primjer 2.

Na Gerberovom posaču iz prethodnoga primjera kinematičkim postupkom odrediti utjecajne linije za reakciju u ležaju  A i moment u presjeku t.

Iz principa virtualnih pomaka slijedi da je na statički određenom nosaču utjecajna linija za neku reakciju ili unutarnju silu jednaka liniji pomaka mehanizma s jednim stupnjem slobode koji nastaje `raskidanjem' odgovarajuće vanjske ili unutarnje veze, ako je na mjestu i u smjeru suprotnom od dogovornog pozitivnog smjera djelovanja sile zadan jedinični pomak.

Dakle, da bismo kinematičkim postupkom konstruirali utjecajnu liniju $\eta_{A}^{}$ za (vertikalnu) reakciju A^v u ležaju A, nepomični zglobni ležaj zamjenjujemo zglobnim ležajem koji omogućava vertikalni pomak. Na taj smo način nosač pretvorili u mehanizam s jednim stupnjem slobode, sastavljen od dva diska -- disk A- C označit ćemo sa  I, a disk C- D sa  II.

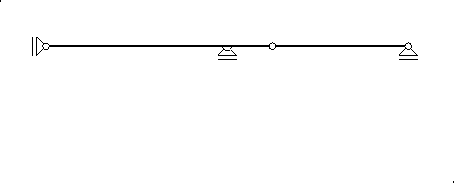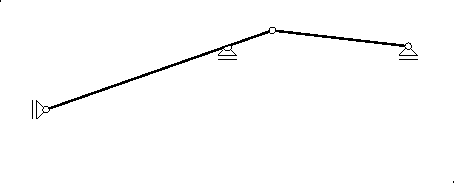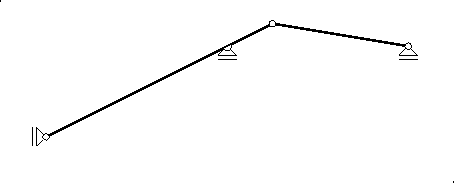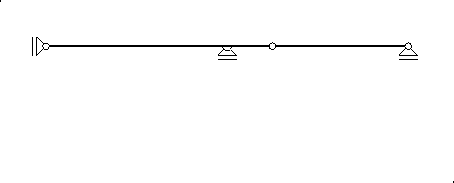
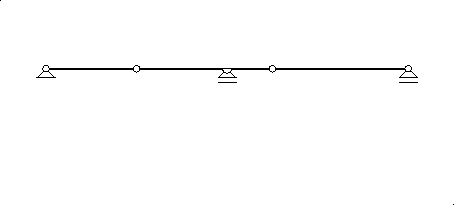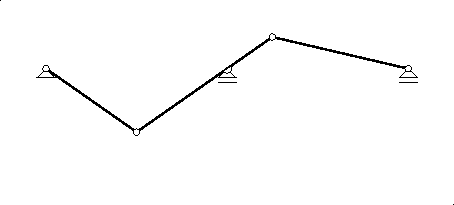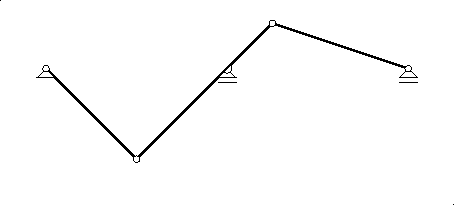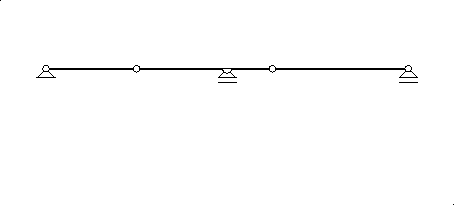
Za konstrukciju plana pomaka treba poznavati apsolutne i relativne polove diskova nastalog mehanizma. Apsolutni pol označavat ćemo arapskom brojkom (na crtežima u kružiću) koja odgovara oznaci diska rimskom brojkom, primjerice, apsolutni pol diska  II imat će oznaku  (2), a relativni pol dvaju diskova parom brojki koje odgovaraju oznakama tih diskova, pa će, primjerice, (1,2) biti oznaka relativnog pola diskova  I i  II. Točka A diska  I može se jedino translatirati po vertikalnom pravcu, jer umetnuti klizni ležaj omogućava samo takav pomak, dok je jedini mogući pomak točke  B translacija po horizontalnom pravcu. Poznato je da (trenutni) apsolutni pol diska mora ležati na pravcu okomitom na pravac mogućeg pomaka neke njegove točke. Prema tome, apsolutni pol  (1) sjecište je horizontalnoga pravca kroz točku  A i vertikalnog pravca kroz točku  B. Horizontala kroz A poklapa se s osi nosača, pa pol  (1) leži u točki  B.

Zglob C relativni je pol  (1,2). Prema teoremu triju polova, apsolutni pol (1), relativni pol (1,2) i apsolutni pol  (2) leže na pravcu. Dopušteni je pomak točke  D diska  II horizontalan, pa pol  (2) mora ležati i na vertikali kroz tu točku. Zaključujemo da pol  (2) leži u točki  D.

Sada možemo na mjestu i na pravcu `raskinute' veze, a u smjeru suprotnom od pretpostavljenoga pozitivnog smjera reakcije A^v, zadati jedinični pomak te nacrtati odgovarajući plan pomaka. Dogovorno uzimamo da se pozitivni smjer sile A^v podudara s pozitivnim smjerom osi y, pa će jedinični pomak točke  A, kojim započinjemo konstrukciju plana (vertikalnih) pomaka, biti prema dolje, u negativnom smjeru osi y; formalno v_{$\mathsf {A}$} = - 1, ali ćemo u nastavku iznose pomaka i kutova zaokreta izražavati u apsolutnim vrijednostima, navodeći uz to eksplicitno njihov smjer -- pišemo, dakle, v_{$\mathsf {A}$} = 1 u smjeru - y.

Disk  I zakreće se oko pola  (1) u smjeru suprotnom od smjera kretanja kazaljke na satu -- kut zaokreta  $\varphi_{{\mathrm{I}}}^{}$ je, dakle, pozitivan. U teoriji malih pomaka, u okviru koje provodimo ovu analizu, vrijedi $\varphi_{k}^{}$ $\approx$ tg $\varphi_{k}^{}$;⁸ štoviše, pisat ćemo $\varphi_{k}^{}$ = tg $\varphi_{k}^{}$, pa je, iz zadanih geometrijskih odnosa,

$$\varphi_{{\mathrm{I}}}^{}$$ = tg $$\varphi_{{\mathrm{I}}}^{}$$ = $${\frac{{v_{\mathsf{A}}}}{{d({\mbox{\color{red}A}},{\mbox{\color{magenta}(1)}})}}}$$ = $${\frac{{1}}{{4}}}$$,

gdje je sa d ( A, (1)) označena udaljenost točke A od pola  (1).

Poznavajući kut zaokreta diska  I, možemo izračunati vertikalni pomak točke  C: v_{$\mathsf {C}$} = $\varphi_{{\mathrm{I}}}^{}$ ^. d ( C, (1)) = ${\tfrac{{1}}{{4}}}$ ^. 1 = 1/4 prema gore, u smjeru + y.

Kako je zglob C relativni pol diskova I i  II, poznat nam je i vertikalni pomak jedne točke diska  II, pa možemo odrediti i kut zaokreta tog diska oko pola  (2): $\varphi_{{\mathrm{II}}}^{}$ = ${\dfrac{{v_{\mathsf{C}}}}{{d({\mbox{\color{red}C}},{\mbox{\color{magenta}(2)}})}}}$ = ${\frac{{1/4}}{{3}}}$ = 1/12 u smjeru vrtnje kazaljke na satu -- formalno, kut  $\varphi_{{\mathrm{II}}}^{}$ je negativan.

Plan (vertikalnih) pomaka diska  I odsječak je pravca koji prolazi pomaknutom točkom  A i polom  (1), a produljuje se sve do pomaknute točke  C. Uočite da se u polu  (1), to jest, nad ležajem  B, plan pomaka ne lomi: A- C je jedan disk. Spojnica pomaknute točke  C i pola  (2) plan je pomaka diska  II. Time je konstrukcija utjecajne linije $\eta_{A}^{}$ dovršena.

[Zadatak: Konstruirajte kinematičkim postupkom utjecajne linije za reakcije u ležajima  B i  D.]

Prelazimo na konstrukciju utjecajne linije za moment u presjeku  t.

Zglob ne prenosi moment savijanja, pa mehanizam s jednim stupnjem slobode za konstrukciju utjecajne linije za M_t nastaje `ugrađivanjem' zgloba u presjek t. Taj je mehanizam sastavljen od tri diska: A- t, s oznakom  I, t- C, s oznakom  II, te C- D, s oznakom  III.

Nepomični je zglobni ležaj  A pol  (1), dok je umetnuti zglob u presjeku  t pol  (1,2). Pol  (2) mora, prema teoremu triju polova, ležati na pravcu kroz polove  (1) i  (1,2), dakle, na osi nosača, a istodobno mora biti i na vertikali kroz ležaj  B, jer je mogući pomak točke  B translacija po osi x. Stoga će pol  (2) biti u točki  B. Na sličan način zaključujemo da je pol  (3) u točki  D: on je, naime, sjecište vertikale kroz ležaj  D s pravcem koji prolazi polom  (2) i zglobom  C, odnosno, polom  (2,3).

Pozitivni je smjer vrtnje momenta u presjeku t pri djelovanju na disk  II jednak smjeru kretanja kazaljke na satu, dok je pri djelovanju na disk  I suprotan od tog smjera. Za konstrukciju utjecajne linije moramo stoga disk  I zakrenuti u smjeru kretanja kazaljke na satu, a disk  II u suprotnom smjeru, i to tako da relativni kut zaokreta $\varphi_{{\mathrm{I-II}}}^{}$ između diskova  I i  II bude jedan, odnosno, kako su posrijedi mali kutovi, tako da bude tg $\varphi_{{\mathrm{I-II}}}^{}$ = 1.

[Zadatak: Konstruirajte kinematičkim postupkom utjecajnu liniju za poprečnu silu u presjeku  t.]

...;⁸

Još su dvije korisne relacije teorije malih pomaka: sin$\varphi_{k}^{}$ $\approx$ $\varphi_{k}^{}$ i cos$\varphi_{k}^{}$ $\approx$ 1.