Neka su
E = 3 . 107 kN/m2 i
![]() = 10-5 K-1.
Poprečni presjek greda vanjskih polja neka je
b/h = 24/60 (cm).
= 10-5 K-1.
Poprečni presjek greda vanjskih polja neka je
b/h = 24/60 (cm).
Vanjska su djelovanja:
K1 = K2 = 90 kN,
q = 60 kN/m'
te
![]() t = 10oC i
t = 10oC i
![]() v = 1 mm.
v = 1 mm.
![\includegraphics[]{mep/mep.21}](img266.png)
Kontinuirani je nosač nosač bez neovisnih translacijskih pomaka, pa su
nepoznanice u inženjerskoj metodi pomaka samo kutovi zaokreta čvorova
2 i
3: ![]() i
i ![]() . (U čvorovima
1
i
4 momenti su poznati, pa zaokrete tih čvorova ne
smatramo nepoznanicama.)
. (U čvorovima
1
i
4 momenti su poznati, pa zaokrete tih čvorova ne
smatramo nepoznanicama.)
Osnovni sistem za metodu pomaka nastat će dodavanjem veza koje sprečavaju nepoznate zaokrete. Time se zadani nosač `raspada' na obostrano upetu gredu 2- 3 te na jednostrano upete grede 1- 2 i 3- 4.
U obzir, naravno, treba uzeti i prepust
4-
5, odnosno,
opterećenje na njemu. Utjecaj tog opterećenja `prenosi'
se na gredu
3-
4 te u proračun ulazi kao dio momenta upetosti
![]() . Sila K2 na kraju prepusta daje
konzolni moment4
M45 = K2 . l45 = 90 kNm.
Uvjet ravnoteže momenata u čvoru
4 daje
M43 = - 90 kNm. Djeluje li nad zglobnim ležajem
jednostrano upete grede koncentrirani moment M, u upetom će ležaju
moment biti
. Sila K2 na kraju prepusta daje
konzolni moment4
M45 = K2 . l45 = 90 kNm.
Uvjet ravnoteže momenata u čvoru
4 daje
M43 = - 90 kNm. Djeluje li nad zglobnim ležajem
jednostrano upete grede koncentrirani moment M, u upetom će ležaju
moment biti
![]() M (pokažite to metodom sila), pa je,
stoga,
M (pokažite to metodom sila), pa je,
stoga,
![]() (K2) = -
(K2) = - ![]() M43 = - 45 kNm.
M43 = - 45 kNm.
Na gredi
3-
4 djeluje i nejednolika temperatura (po visini
poprečnog presjeka). Doprinos te promjenjive temperature momentu
upetosti je
![]() (
(![]() t) = -
t) = - ![]() EI
EI ![]() = - 32, 4 kNm
(za zadani je poprečni presjek
I = 0, 00432 m4),
te je ukupni moment upetosti
= - 32, 4 kNm
(za zadani je poprečni presjek
I = 0, 00432 m4),
te je ukupni moment upetosti
| = |
||
| = - |
||
| = - 45, 0 - 32, 4 = - 77, 4 kNm. |
Na gredu 1- 2 djeluje sila K1 (sa a i b označit ćemo udaljenosti od ležaja 1 do hvatišta sile i od hvatišta sile do ležaja 2), a zadan je i prisilni vertikalni pomak ležaja 1, pa je
| = |
||
= 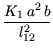 - - 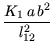 |
||
| = - 40, 0 - 43, 2 = - 83, 2 kNm. |
Momenti upetosti na obostrano upetoj gredi 2- 3 su:
= 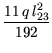 = 55, 0 kNm, = 55, 0 kNm, |
||
| = |
Osnovni se sistem, zbog dodanih veza koje sprečavaju zaokrete čvorova, ne ponaša jednako kao i zadani. Treba stoga na osnovnom sistemu zadati `prisilne' zaokrete čvorova koji će odgovarati onima u zadanom sistemu. Momenti koje u priključenim gredama izazovu ti zaokreti uravnotežuju razliku momenata upetosti u pojedinim čvorovima -- kuteve zaokreta možemo, dakle, izračunati iz jednadžbi ravnoteže momenata u čvorovima.
Zaokreti čvorova i i j za kuteve ![]() i
i ![]() uzrokuju
u čvorovima obostrano upete grede momente
uzrokuju
u čvorovima obostrano upete grede momente
| mij* | = kij* (4 |
|
| mji* | = kij* (2 |
Umjesto stvarnih krutosti kij* uvodimo proračunske vrijednosti
kij = ![]() . Za E0I0 biramo veličine koje
se najčešće pojavljuju; u ovom je primjeru jednostavno
E0I0 = EI, pa su proračunske krutosti
k12 = 1/l12 = 1/3,
k23 = 2/l23 = 1/2,
k34 = 1/l34 = 1/3.
. Za E0I0 biramo veličine koje
se najčešće pojavljuju; u ovom je primjeru jednostavno
E0I0 = EI, pa su proračunske krutosti
k12 = 1/l12 = 1/3,
k23 = 2/l23 = 1/2,
k34 = 1/l34 = 1/3.
Ukupni momenti na krajevima grednih elemenata zbroj su momenata od zaokreta čvorova i momenata upetosti:
| M21 | = 3 k12 |
|
| M23 | = 4 k23 |
|
| M32 | = 2 k23 |
|
| M34 | = 3 k34 |
Uvrštavanje u jednadžbe ravnoteže momenata u čvorovima 2 i 3:
| = M21 + M23 = 0, | ||
| = M32 + M34 = 0, |
| 3 |
||
Koeficijenti u jednadžbama nastali su zbrajanjem proračunskih,
a ne stvarnih krutosti, pa izračunate vrijednosti
![]() i
i ![]() nisu stvarni kutevi zaokreta.5
Međutim, kako su i u izrazima (
nisu stvarni kutevi zaokreta.5
Međutim, kako su i u izrazima (![]() ) za momente na
krajevima elemenata proračunske vrijednosti kij,
uvrštavanje izračunatih veličina
) za momente na
krajevima elemenata proračunske vrijednosti kij,
uvrštavanje izračunatih veličina ![]() i
i ![]() u te
izraze daje stvarne veličine momenata:
u te
izraze daje stvarne veličine momenata:
| M21 | = - 85, 425 kNm | |
| M23 | = 85, 425 kNm | |
| M32 | = 42, 525 kNm | |
| M34 | = - 42, 525 kNm |
![\includegraphics[]{mep/mep.22}](img297.png)