Pogledajmo što predstavljaju pojedine funkcije ![]() od kojih je sastavljeno rješenje 2.26.
od kojih je sastavljeno rješenje 2.26.
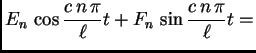
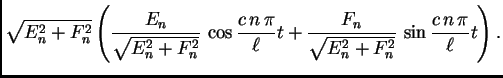
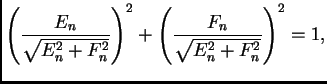
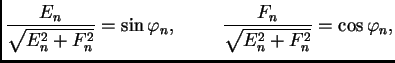
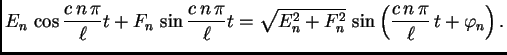
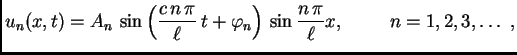
Za ![]() imamo
imamo
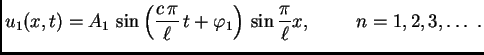
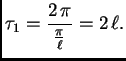
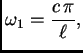
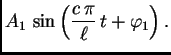
Za ![]() imamo
imamo
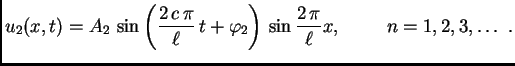
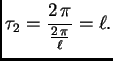
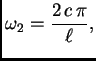
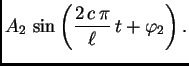
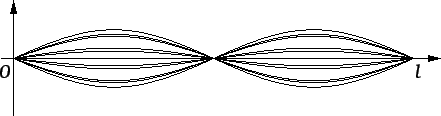
Za ![]() imamo čvorove
imamo čvorove
![]() frekvencija
titranja je
frekvencija
titranja je
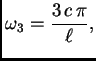

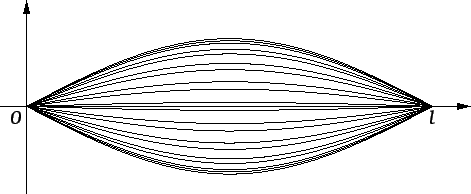
Ovakva titranja se zovu stojni
valovi.
Stvarno slobodno titranje je superpozicija ovakvih titranja. Kad se
radi o napetoj žici, ona prilikom titranja proizvodi ton. Broj
![]() se zove frekvencija osnovnog tona, a ostale
frekvencije se zovu frekvencije viših
harmonika. Amplitude
viših harmonika vrlo brzo opadaju prema nuli. Njihova distribucija
daje boju proizvedenom tonu. Primijetimo na kraju da je frekvencija
osnovnog tona
se zove frekvencija osnovnog tona, a ostale
frekvencije se zovu frekvencije viših
harmonika. Amplitude
viših harmonika vrlo brzo opadaju prema nuli. Njihova distribucija
daje boju proizvedenom tonu. Primijetimo na kraju da je frekvencija
osnovnog tona
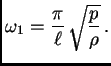
Rješenje. Rubni i početni uvjeti su kao u primjeru 2.15, a jednadžba glasi
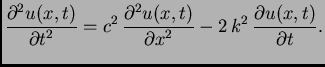
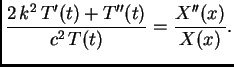
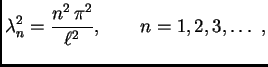
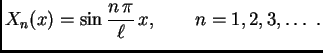
Pretpostavimo da je otpor dovoljno malen tako da je
![]() Tada je
Tada je
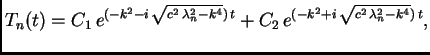
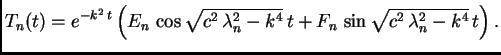
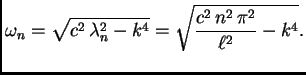
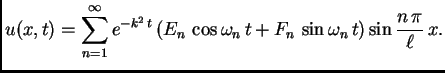
Faktor
![]() teži k nuli kad
teži k nuli kad
![]() Zato
titranje postaje sve slabije kako
Zato
titranje postaje sve slabije kako ![]() raste. Tako imamo prigušene
oscilacije.
raste. Tako imamo prigušene
oscilacije.