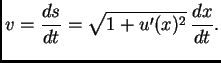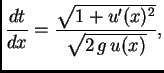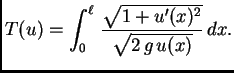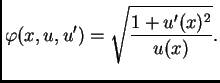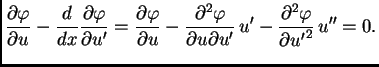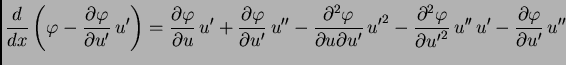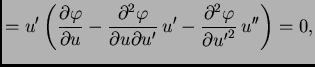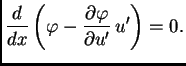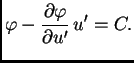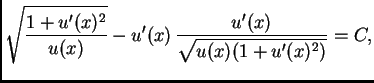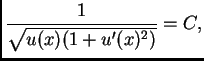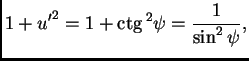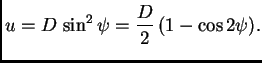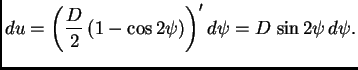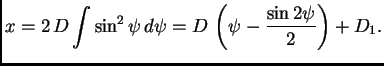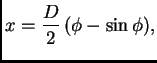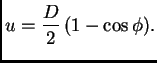Next: Višedimenzionalni problemi
Up: Varijacijske metode
Previous: Varijacijski princip
Sadržaj
Indeks
Varijacijski račun
U 2.4.1 smo razmatrali problem minimizacije funkcionala
energije određenog rubnog problema. Ovdje ćemo razmatrati problem
minimizacije općenitijeg funkcionala.
Neka je dana neprekidno derivabilna funkcija od tri varijable
Neka je 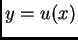 i
i 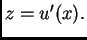 Tada imamo kompoziciju
funkcija (složenu funkciju) od jedne varijable
U vezi s tom funkcijom možemo promatrati sljedeći funkcional
Ovo je općenitiji funkcional od onih koje smo promatrali. Na pr. ako
stavimo
onda kompozicija kao gore daje funkcional energije (2.39).
Tada imamo kompoziciju
funkcija (složenu funkciju) od jedne varijable
U vezi s tom funkcijom možemo promatrati sljedeći funkcional
Ovo je općenitiji funkcional od onih koje smo promatrali. Na pr. ako
stavimo
onda kompozicija kao gore daje funkcional energije (2.39).
Osim same formule, važno je odrediti domenu funkcionala. Kao što se
iz formule vidi, funkcional 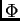 pridružuje funkciji
pridružuje funkciji 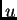 broj. Važno je definirati kojem skupu pripada funkcija
broj. Važno je definirati kojem skupu pripada funkcija 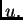 To
naravno ovisi o problemu o kojem se radi. Pretpostavimo da je
funkcional
To
naravno ovisi o problemu o kojem se radi. Pretpostavimo da je
funkcional 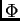 definiran na skupu
definiran na skupu
Skup 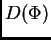 je
vektorski prostor, jer je bilo koja linearna kombinacija elemenata iz
je
vektorski prostor, jer je bilo koja linearna kombinacija elemenata iz
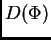 opet element iz
opet element iz 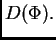 Elemente iz
Elemente iz 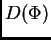 ćemo zvati
dopustivim funkcijama.
ćemo zvati
dopustivim funkcijama.
Posebno nas interesiraju funkcije na kojima funkcional poprima
minimalnu ili maksimalnu vrijednost. Svaka takva funkcija se zove
ekstremala. Nađimo sada uvjet koji
treba ispunjavati
funkcija 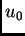 da bude ekstremala funkcionala
da bude ekstremala funkcionala 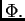 U tu svrhu
stavimo
U tu svrhu
stavimo
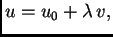 gdje je
gdje je 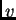 dopustiva funkcija.
dopustiva funkcija.
je
funkcija od 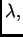 i za
i za 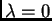 ona ima ekstrem. Budući da je
funkcija
neprekidno derivabilna, to znači da mora biti
ona ima ekstrem. Budući da je
funkcija
neprekidno derivabilna, to znači da mora biti
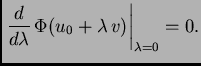 |
(2.38) |
Kako je 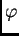 neprekidno derivabilna, imamo
Preciznije
Zbog (2.40) imamo
neprekidno derivabilna, imamo
Preciznije
Zbog (2.40) imamo
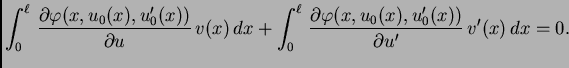 |
(2.39) |
Jednom parcijalno integrirajmo drugi integral
Funkcija
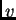 je dopustiva, pa je
je dopustiva, pa je 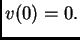 Tako imamo
Kad to uvrstimo u (2.41), dobivamo
Tako imamo
Kad to uvrstimo u (2.41), dobivamo
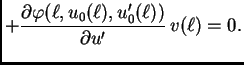 |
(2.40) |
Ova jednakost vrijedi za svaku dopustivu funkciju, pa i za takve za
koje je
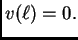 Za takve dopustive funkcije imamo
Na osnovu leme 2 slijedi
ili kraće
Za takve dopustive funkcije imamo
Na osnovu leme 2 slijedi
ili kraće
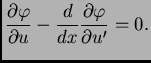 |
(2.41) |
Ako se s time vratimo u jednadžbu (2.42), te zbog
proizvoljnosti dopustive funkcije 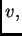 uzmemo
uzmemo 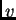 takvu da je
takvu da je
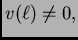 slijedi da mora vrijediti također
Ova jednakost se zove prirodni uvjet na rubu
slijedi da mora vrijediti također
Ova jednakost se zove prirodni uvjet na rubu 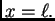
Jednadžba (2.43) se zove Eulerova diferencijalna
jednadžba za
dani funkcional. Dakle, da bi funkcija 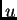 bila ekstremala funkcionala
bila ekstremala funkcionala
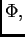 nužno mora zadovoljavati pripadnu Eulerovu diferencijalnu
jednadžbu. To je nužan uvjet, ali ne i dovoljan. Dovoljne uvjete
ovdje nećemo razmatrati. Napomenimo da se iz prirode problema
često može zaključiti da li ekstremala postoji ili ne. Ako postoji,
i ima neprekidne derivacije dovoljno visokog reda, onda je dovoljno
naći rješenje Eulerove jednadžbe, koje zadovoljava rubne uvjete.
nužno mora zadovoljavati pripadnu Eulerovu diferencijalnu
jednadžbu. To je nužan uvjet, ali ne i dovoljan. Dovoljne uvjete
ovdje nećemo razmatrati. Napomenimo da se iz prirode problema
često može zaključiti da li ekstremala postoji ili ne. Ako postoji,
i ima neprekidne derivacije dovoljno visokog reda, onda je dovoljno
naći rješenje Eulerove jednadžbe, koje zadovoljava rubne uvjete.
Primjer 2.19
Problem brahistohrone. Interesira nas koji
oblik putanje
treba izabrati tako da se za najkraće vrijeme, u polju sile teže,
stigne iz točke
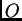
u točku
Krivulja s tim svojstvom se zove
brahistohrona.
2.2
Rješenje. Zakon o sačuvanju energije glasi
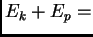
konst.
Nadalje
Predznak
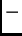
dolazi stoga što smo pozitivni dio osi
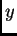
okrenuli
prema dolje. Tako je
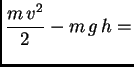
konst.
U točki
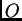
je
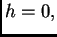
i
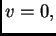
pa slijedi da je konstanta jednaka
nuli. Odatle
jer ćemo u daljnjem visinu označavati s
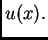
Zadatak je naći
funkciju
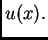
S druge strane brzina je
Odatle je
pa je vrijeme gibanja po krivulji
Od svih puteva
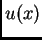
treba izabrati onaj uz koji ovaj funkcional
poprima najmanju vrijednost uz uvjete
Budući da konstanta
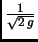
ne utječe na to da li je
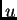
ekstremala ili
ne, možemo uzeti
Budući da u
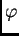
ne dolazi eksplicitno
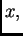
Eulerova jednadžba
glasi
S druge strane
jer je izraz u zagradi upravo lijeva strana Eulerove jednadžbe. Dakle
Odatle
U našem slučaju
tj.
Stavimo
gdje je
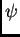
parametar.
pa je
Sada treba
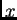
izraziti kao funkciju od
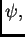
pa ćemo tako dobiti
parametarski određenu traženu krivulju.
Isto tako
Tako je
Odatle
Mora biti
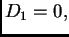
da bi istovremeno
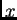
i
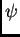
težili k
nuli. Stavimo
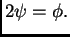
Tada je
dok je
Konstanta
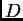
se određuje iz
preostalog rubnog uvjeta
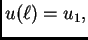
ili preciznije
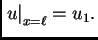
Ove parametarske jednadžbe
predstavljaju cikloidu.





Next: Višedimenzionalni problemi
Up: Varijacijske metode
Previous: Varijacijski princip
Sadržaj
Indeks
2001-10-26
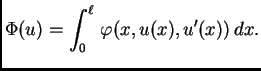
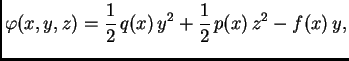
![]() pridružuje funkciji
pridružuje funkciji ![]() broj. Važno je definirati kojem skupu pripada funkcija
broj. Važno je definirati kojem skupu pripada funkcija ![]() To
naravno ovisi o problemu o kojem se radi. Pretpostavimo da je
funkcional
To
naravno ovisi o problemu o kojem se radi. Pretpostavimo da je
funkcional ![]() definiran na skupu
definiran na skupu
![]() da bude ekstremala funkcionala
da bude ekstremala funkcionala ![]() U tu svrhu
stavimo
U tu svrhu
stavimo
![]() gdje je
gdje je ![]() dopustiva funkcija.
dopustiva funkcija.
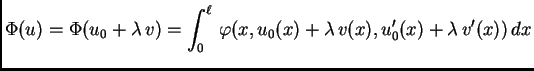
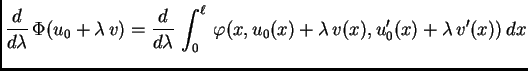
![$\displaystyle = \int_0^{\ell}\,
\frac{d}{d\lambda}\,
\varphi(x,u_0(x)+\lambda\...
...i}{\partial u}\,v(x) + \frac{\partial
\varphi}{\partial u'}\,v'(x)\right]\,dx.$](img1899.png)
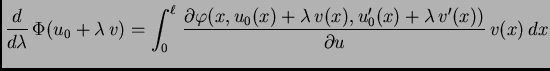
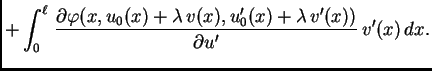
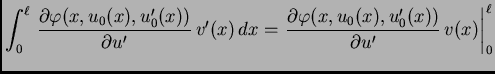
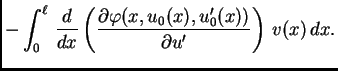
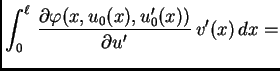
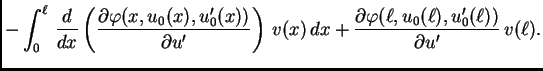
![$\displaystyle \int_0^{\ell}\,\left[\frac{\partial \varphi(x,u_0(x),u'_0(x))}{\p...
...(\frac{\partial \varphi(x,u_0(x),u'_0(x))}{\partial u'}\right)\right]\,v(x)\,dx$](img1907.png)
![$\displaystyle \int_0^{\ell}\,\left[\frac{\partial
\varphi(x,u_0(x),u'_0(x))}{\...
...{\partial \varphi(x,u_0(x),u'_0(x))}{\partial
u'}\right)\right]\,v(x)\,dx = 0.$](img1909.png)
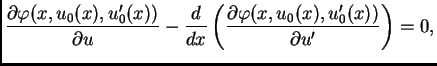
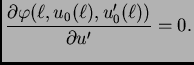
![]() bila ekstremala funkcionala
bila ekstremala funkcionala
![]() nužno mora zadovoljavati pripadnu Eulerovu diferencijalnu
jednadžbu. To je nužan uvjet, ali ne i dovoljan. Dovoljne uvjete
ovdje nećemo razmatrati. Napomenimo da se iz prirode problema
često može zaključiti da li ekstremala postoji ili ne. Ako postoji,
i ima neprekidne derivacije dovoljno visokog reda, onda je dovoljno
naći rješenje Eulerove jednadžbe, koje zadovoljava rubne uvjete.
nužno mora zadovoljavati pripadnu Eulerovu diferencijalnu
jednadžbu. To je nužan uvjet, ali ne i dovoljan. Dovoljne uvjete
ovdje nećemo razmatrati. Napomenimo da se iz prirode problema
često može zaključiti da li ekstremala postoji ili ne. Ako postoji,
i ima neprekidne derivacije dovoljno visokog reda, onda je dovoljno
naći rješenje Eulerove jednadžbe, koje zadovoljava rubne uvjete.

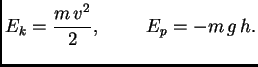
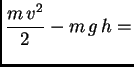 konst.
konst.