




Next: Gauss-Seidelova metoda
Up: Rješavanje sustava jednadžbi
Previous: Osnovni problem.
Sadržaj
Indeks
Jacobijeva metoda
Pretpostavimo da su elementi na glavnoj dijagonali matrice 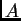 različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo
različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo 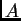 kako slijedi
kako slijedi
gdje je
Tako su 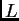 donja,
donja, 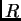 gornja trokutasta s nulama na glavnoj dijagonali, a
gornja trokutasta s nulama na glavnoj dijagonali, a 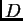 je dijagonalna
matrica. Ako stavimo
imamo iterativni postupak oblika
Budući da su elementi na glavnoj dijagonali matrice
je dijagonalna
matrica. Ako stavimo
imamo iterativni postupak oblika
Budući da su elementi na glavnoj dijagonali matrice 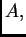 a prema tome
i matrice
a prema tome
i matrice 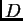 različiti od nule, postoji
različiti od nule, postoji 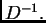 Inverz od
dijagonalne matrice se vrlo lako računa. Iz
Inverz od
dijagonalne matrice se vrlo lako računa. Iz
![$ D=[\delta_{ij}\,a_{ii}]$](img2699.png) slijedi
slijedi
![$ D^{-1}=[\frac{\delta_{ij}}{a_{ii}}].$](img2700.png) Tako gornju
jednadžbu možemo pomnožiti s lijeva s
Tako gornju
jednadžbu možemo pomnožiti s lijeva s 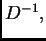 pa imamo sljedeći
algoritam.
pa imamo sljedeći
algoritam.
Algoritam 5
(Jacobijeva metoda)
Proizvoljno izaberemo početnu aproksimaciju
i zatim računamo sljedeće aproksimacije
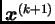
po
formuli
odnosno
gdje je
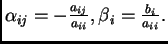
Budući da dijelimo s
 poželjno je, ako je to moguće, poredati retke u matrici
poželjno je, ako je to moguće, poredati retke u matrici 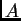 (jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.
(jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.





Next: Gauss-Seidelova metoda
Up: Rješavanje sustava jednadžbi
Previous: Osnovni problem.
Sadržaj
Indeks
2001-10-26
![]() različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo
različiti od nule (ako je potrebno, premještanjem redaka u
regularnoj matrici se to uvijek može postići).
Rastavimo ![]() kako slijedi
kako slijedi
![\begin{displaymath}
% latex2html id marker 38594
L = \left[
\begin{array}{ccccc...
...n\,1} & a_{n\,2} & \cdots & a_{n\,n-1} & 0
\end{array}\right],\end{displaymath}](img2694.png)
![\begin{displaymath}
% latex2html id marker 38596
D = \left[
\begin{array}{cccc}...
... & a_{n-1\,n} \\
0 & 0 & \cdots & 0 & 0
\end{array}\right].\end{displaymath}](img2695.png)
![% latex2html id marker 38621
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}
\right],$](img2702.png)
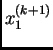
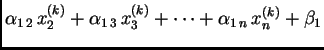
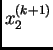
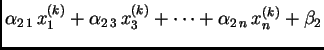
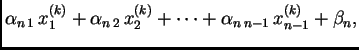
![]() poželjno je, ako je to moguće, poredati retke u matrici
poželjno je, ako je to moguće, poredati retke u matrici ![]() (jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.
(jednadžbe
u sustavu) tako da svaki element na glavnoj dijagonali bude po apsolutnoj
vrijednosti veći od sume apsolutnih vrijednosti ostalih elemenata u
retku u kojem se nalazi.