![% latex2html id marker 38655
$\displaystyle \boldsymbol{x}^{(k)}=\left[
\begin{array}{c}
x_1^{(k)} \\ x_2^{(k)} \\ \vdots \\ x_n^{(k)}
\end{array}
\right]$](img2712.png)
Gauss-Seidelova metoda je poboljšanje Jacobijeve metode u sljedećem smislu.
Pod pretpostavkom da je
![% latex2html id marker 38655
$\displaystyle \boldsymbol{x}^{(k)}=\left[
\begin{array}{c}
x_1^{(k)} \\ x_2^{(k)} \\ \vdots \\ x_n^{(k)}
\end{array}
\right]$](img2712.png)
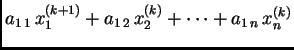 |
|||
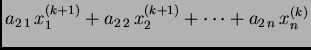 |
|||
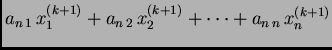 |
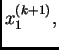 koji smo izračunali iz prve jednadžbe pomoću
komponenti
koji smo izračunali iz prve jednadžbe pomoću
komponenti 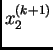 koristimo u
trećoj, četvrtoj, ...,
koristimo u
trećoj, četvrtoj, ...,
![% latex2html id marker 38709
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}
\right],$](img2726.png)
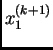 |
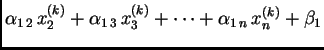 |
||
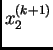 |
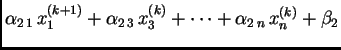 |
||
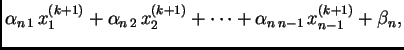 |
Rješenje. Radi jednostavnosti ćemo radije vektorstupac rješenja pisati u
obliku
![]() Ako počnemo s
Ako počnemo s
![]() Jacobijeva metoda daje sustav
Jacobijeva metoda daje sustav