Imamo
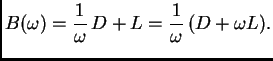
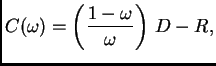
![$\displaystyle \frac{1}{\omega{}}\,(D +
\omega{}L)\,\boldsymbol{x}^{(k+1)} =
\...
...mega{}}{\omega{}}\right)\,D -
R\right]\,\boldsymbol{x}^{(k)} + \boldsymbol{b}.$](img2806.png)
![% latex2html id marker 39001
$\displaystyle \boldsymbol{x}^{(0)}=\left[
\begin{array}{c}
x_1^{(0)} \\ x_2^{(0)} \\ \vdots \\ x_n^{(0)}
\end{array}
\right],$](img2809.png)
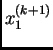 |
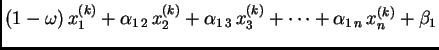 |
||
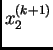 |
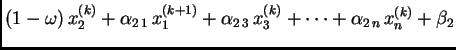 |
||
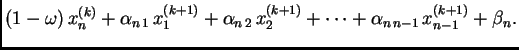 |
Primijetimo da za
![]() SOR metoda postaje Gauss-Seidelova
metoda.
SOR metoda postaje Gauss-Seidelova
metoda.
Broj ![]() treba uzeti tako da je
treba uzeti tako da je
![]() Optimalna
vrijednost ovisi o konkretnom problemu koji se rješava.
Optimalna
vrijednost ovisi o konkretnom problemu koji se rješava.
Rješenje. Jacobijeva OR metoda ne daje ništa bolje rezultate kad se uzme
![]() Gauss-Seidelova OR metoda za
Gauss-Seidelova OR metoda za
![]() daje
daje